Понятие дифференциального уравнения. Общее и частное решения

Учреждение образования «Белорусская государственная

Сельскохозяйственная академия»

Кафедра высшей математики

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА

Конспект лекции для студентов бухгалтерского факультета

заочной формы получения образования (НИСПО)

Горки, 2013

Дифференциальные уравнения первого порядка

Понятие дифференциального уравнения. Общее и частное решения

При изучении различных явлений часто не удаётся найти закон, который непосредственно связывает независимую переменную и искомую функцию, но можно установить связь между искомой функцией и её производными.

Соотношение, связывающее независимую переменную, искомую функцию и её производные, называется дифференциальным уравнением:

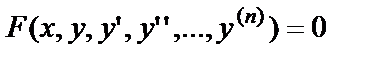. (1)

Здесь x – независимая переменная, y – искомая функция, 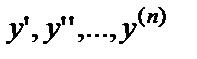- производные искомой функции. При этом в соотношении (1) обязательно наличие хотя бы одной производной.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.

Рассмотрим дифференциальное уравнение

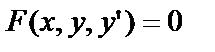. (2)

Так в это уравнение входит производная только первого порядка, то оно называется дифференциальным уравнением первого порядка.

Если уравнение (2) можно разрешить относительно производной и записать в виде

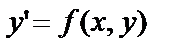, (3)

то такое уравнение называется дифференциальным уравнением первого порядка в нормальной форме.

Во многих случаях целесообразно рассматривать уравнение вида

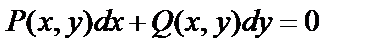, (4)

которое называется дифференциальным уравнением первого порядка, записанным в дифференциальной форме.

Так как 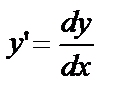, то уравнение (3) можно записать в виде 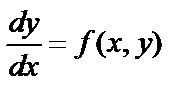или 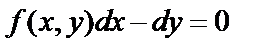, где можно считать 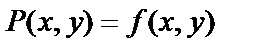и 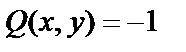. Это означает, что уравнение (3) преобразовано в уравнение (4).

Запишем уравнение (4) в виде 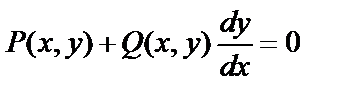. Тогда 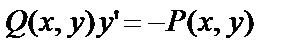, , 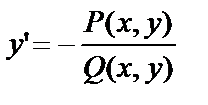, 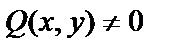где можно считать 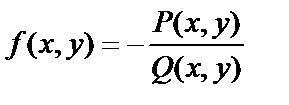, т.е. получено уравнение вида (3). Таким образом, уравнения (3) и (4) равносильны.

Решением дифференциального уравнения (2) или (3) называется любая функция 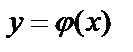, которая при подстановке её в уравнение (2) или (3) обращает его в тождество:

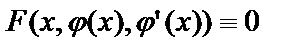или .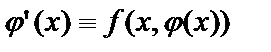

Процесс нахождения всех решений дифференциального уравнения называется его интегрированием, а график решения 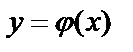дифференциального уравнения называется интегральной кривой этого уравнения.

Если решение дифференциального уравнения получено в неявном виде 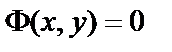, то оно называется интегралом данного дифференциального уравнения.

Общим решением дифференциального уравнения первого порядка называется семейство функций вида 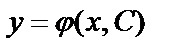, зависящее от произвольной постоянной С, каждая из которых является решением данного дифференциального уравнения при любом допустимом значении произвольной постоянной С. Таким образом, дифференциальное уравнение имеет бесчисленное множество решений.

Частным решением дифференциального уравнения называется решение, получаемое из формулы общего решения при конкретном значении произвольной постоянной С, включая .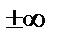

1. Задача Коши и её геометрическая интерпретация

Уравнение (2) имеет бесчисленное множество решений. Чтобы из этого множества выделить одно решение, которое называется частным, нужно задать некоторые дополнительные условия.

Задача отыскания частного решения уравнения (2) при заданных условиях называется задачей Коши. Эта задача является одной из важнейших в теории дифференциальных уравнений.

Формулируется задача Коши следующим образом: среди всех решений уравнения (2) найти такое решение 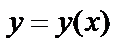, в котором функция 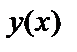принимает заданное числовое значение 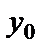, если независимая переменная x принимает заданное числовое значение 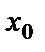, т.е.

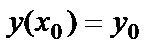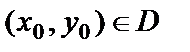, , (5)

где D – область определения функции .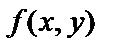

Значение 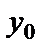называется начальным значением функции, а 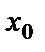– начальным значением независимой переменной. Условие (5) называется начальным условием или условием Коши.

С геометрической точки зрения задачу Коши для дифференциального уравнения (2) можно сформулировать следующим образом: из множества интегральных кривых уравнения (2) выделить ту, которая проходит через заданную точку .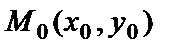

1. Дифференциальные уравнения с разделяющимися переменными

Одним из простейших видов дифференциальных уравнений является дифференциальное уравнение первого порядка, не содержащее искомой функции:

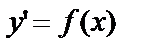. (6)

Учитывая, что 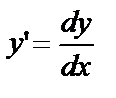, запишем уравнение в виде 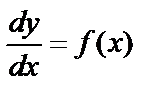или 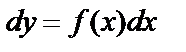. Интегрируя обе части последнего уравнения, получим: 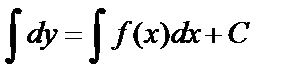или

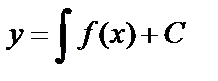. (7)

Таким образом, (7) является общим решением уравнения (6).

Пример 1. Найти общее решение дифференциального уравнения .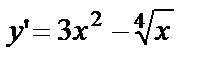

Решение. Запишем уравнение в виде 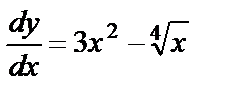или 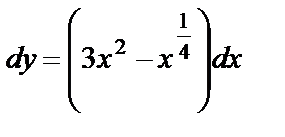. Проинтегрируем обе части полученного уравнения: 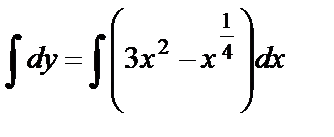, 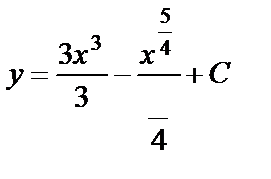. Окончательно запишем .

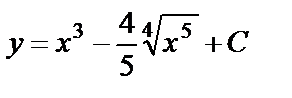Пример 2. Найти решение уравнения 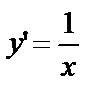при условии .

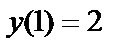Решение. Найдём общее решение уравнения: 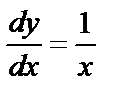, , 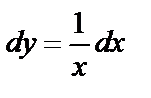, 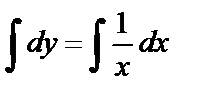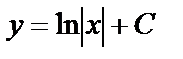. По условию 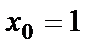, 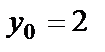. Подставим в общее решение: 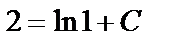или 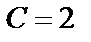. Найденное значение произвольной постоянной подставим в формулу общего решения: 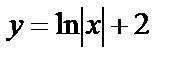. Это и есть частное решение дифференциального уравнения, удовлетворяющее заданному условию.

Уравнение

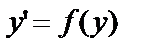(8)

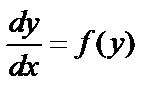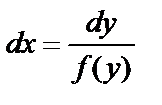Называется дифференциальным уравнением первого порядка, не содержащим независимой переменной. Запишем его в виде или . Проинтегрируем обе части последнего уравнения: 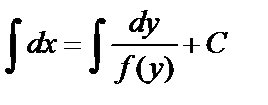или 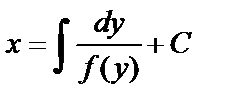- общее решение уравнения (8).

Пример. Найти общее решение уравнения .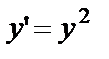

Решение. Запишем это уравнение в виде: 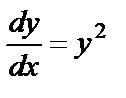или 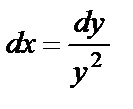. Тогда 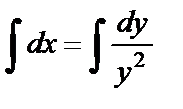, , 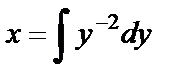, 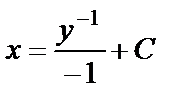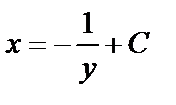. Таким образом, 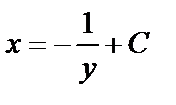– общее решение данного уравнения.

Уравнение вида

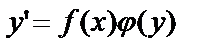(9)

интегрируется с помощью разделения переменных. Для этого уравнение запишем в виде 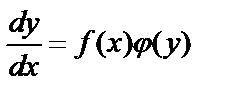, а затем с помощью операций умножения и деления приводим его к такой форме, чтобы в одну часть входила только функция от х и дифференциал dx, а во вторую часть – функция от у и дифференциал dy. Для этого обе части уравнения нужно умножить на dx и разделить на 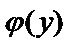. В результате получим уравнение

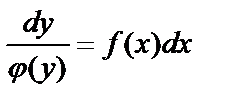, (10)

в котором переменные х и у разделены. Проинтегрируем обе части уравнения (10): 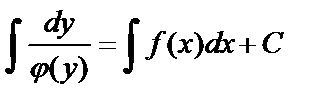. Полученное соотношение является общим интегралом уравнения (9).

Пример 3. Проинтегрировать уравнение .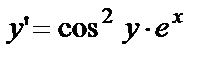

Решение. Преобразуем уравнение и разделим переменные: 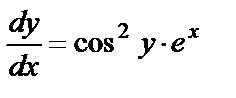, 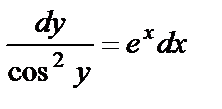. Проинтегрируем: 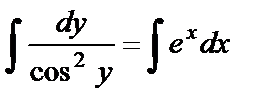, 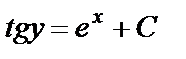или – общий интеграл данного уравнения. .

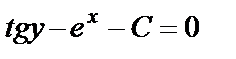Пусть уравнение задано в виде

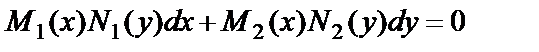. (11)

Такое уравнение называется дифференциальным уравнением первого порядка с разделяющимися переменными в симметрической форме.

Для разделения переменных нужно обе части уравнения разделить на :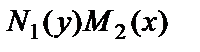

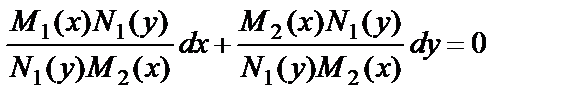. (12)

Полученное уравнение называется дифференциальным уравнением с разделёнными переменными. Проинтегрируем уравнение (12):

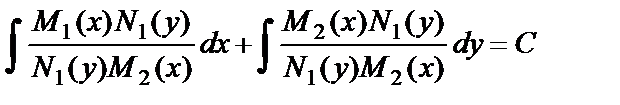. (13)

Соотношение (13) является общим интегралом дифференциального уравнения (11).

Пример 4. Проинтегрировать дифференциальное уравнение .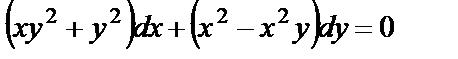

Решение. Запишем уравнение в виде

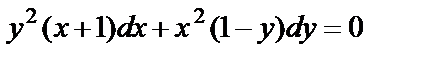и разделим обе его части на 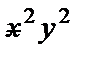, 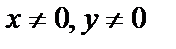. Полученное уравнение: 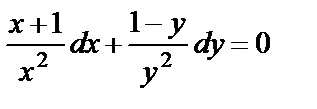является уравнением с разделёнными переменными. Проинтегрируем его:

, ,

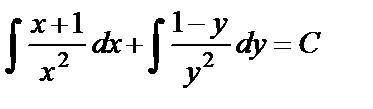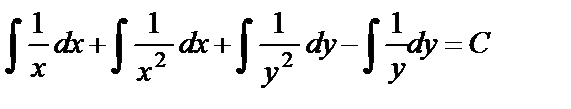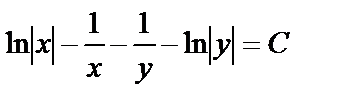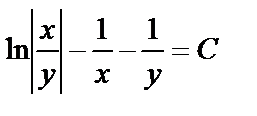, . Последнее равенство является общим интегралом данного дифференциального уравнения.

Пример 5. Найти частное решение дифференциального уравнения 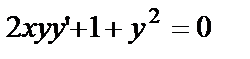, удовлетворяющее условию .

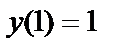Решение. Учитывая, что 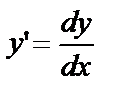, запишем уравнение в виде 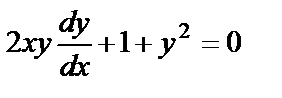или 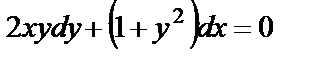. Разделим переменные: 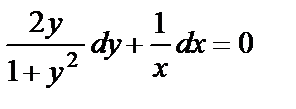. Проинтегрируем это уравнение: 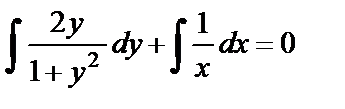, , 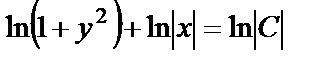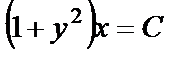. Полученное соотношение является общим интегралом данного уравнения. По условию 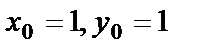. Подставим в общий интеграл и найдём С: 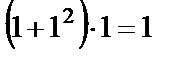, С=1. Тогда выражение 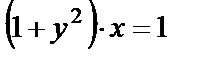является частным решением данного дифференциального уравнения, записанным в виде частного интеграла.

1. Линейные дифференциальные уравнения первого порядка

Уравнение

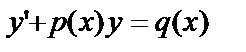(14)

называется линейным дифференциальным уравнением первого порядка. Неизвестная функция 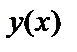и её производная входят в это уравнение линейно, а функци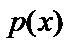и и 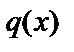непрерывны.

Если 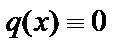, то уравнение

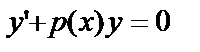(15)

называется линейным однородным. Если 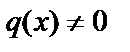, то уравнение (14) называется линейным неоднородным.

Для нахождения решения уравнения (14) обычно используют метод подстановки (Бернулли), суть которого в следующем.

Решение уравнения (14) будем искать в виде произведения двух функций

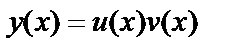, (16)

где 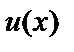и 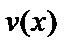- некоторые непрерывные функции. Подставим 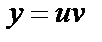и производную 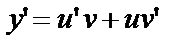в уравнение (14):

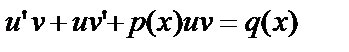или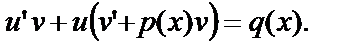

Функцию v будем подбирать таким образом, чтобы выполнялось условие 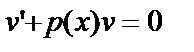. Тогда 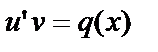. Таким образом, для нахождения решения уравнения (14) нужно решить систему дифференциальных уравнений

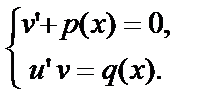
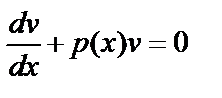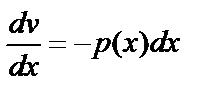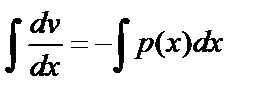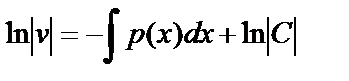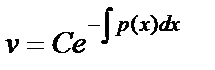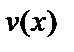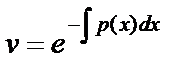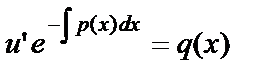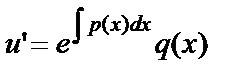Первое уравнение системы является линейным однородным уравнением и решить его можно методом разделения переменных: , , , , . В качестве функции можно взять одно из частных решений однородного уравнения, т.е. при С=1: . Подставим во второе уравнение системы: или .Тогда 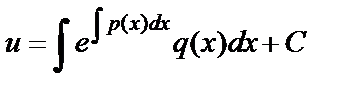. Таким образом, общее решение линейного дифференциального уравнения первого порядка имеет вид .

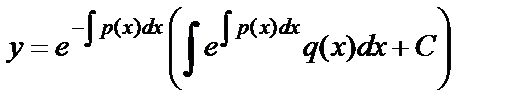Пример 6. Решить уравнение .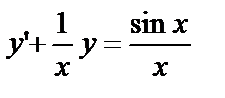

Решение. Решение уравнения будем искать в виде 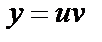. Тогда 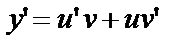. Подставим в уравнение:

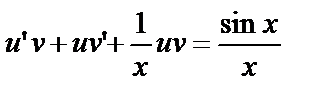или 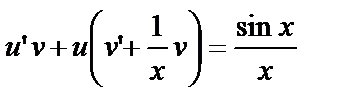. Функцию v выберем таким образом, чтобы выполнялось равенство 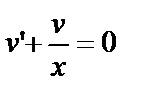. Тогда 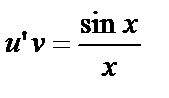. Решим первое из этих уравнений методом разделения переменных: 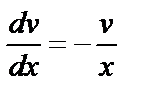, , 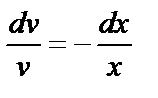, , 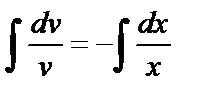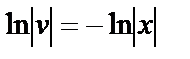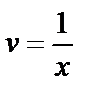. Функцию v подставим во второе уравнение: 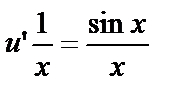, , 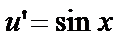, 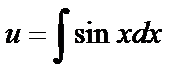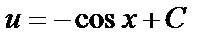. Общим решением данного уравнения является .

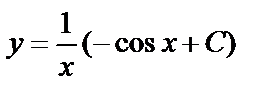Вопросы для самоконтроля знаний

1. Что называется дифференциальным уравнением?

2. Что называется порядком дифференциального уравнения?

3. Какое дифференциальное уравнение называется дифференциальным уравнением первого порядка?

4. Как записывается дифференциальное уравнение первого порядка в дифференциальной форме?

5. Что называется решением дифференциального уравнения?

6. Что называется интегральной кривой?

7. Что называется общим решением дифференциального уравнения первого порядка?

8. Что называется частным решением дифференциального уравнения?

9. Как формулируется задача Коши для дифференциального уравнения первого порядка?

10. Какова геометрическая интерпретация задачи Коши?

11. Как записывается дифференциальное уравнение с разделяющимися переменными в симметрической форме?

12. Какое уравнение называется линейным дифференциальным уравнением первого порядка?

13. Каким методом можно решить линейное дифференциальное уравнение первого порядка и в чём суть этого метода?