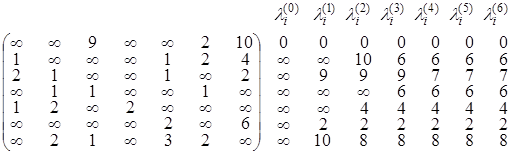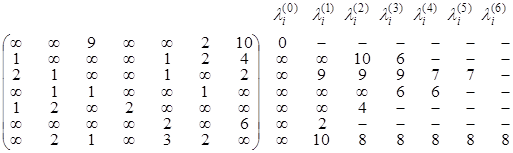Минимальные пути (маршруты) в нагруженных орграфах (графах)
Пусть G=(V, E) – орграф. Рассмотрим функцию f: E→ R, которая каждой дуге e Î E орграфа ставит в соответствие некоторое действительное число f(e). Функцию f называют весовой функцией, а орграф G, на дугах которого она определена, называют нагруженным (взвешенным).
Значение f(e) называют длиной дуги e. Если π – путь в G, то f(π) в нагруженном графе будет обозначать сумму длин входящих в π дуг, причем каждая дуга учитывается столько раз, сколько раз она входит в путь. Величина f(π) называется длиной пути в нагруженном орграфе.
Замечание.Если f(e)=1 для каждого e Î E, то f(π) выражает длину пути в ненагруженном орграфе.
Сформулировать определение нагруженного графа и длины маршрута в нем самостоятельно.
Опр.Путь (маршрут) в нагруженном орграфе (графе) G из вершины v в вершину w (соединяющий v и w), где v≠w, называется минимальным , если он имеет минимальную длину среди всех путей (маршрутов) орграфа (графа) G изv в w (соединяющих v и w).
Если в нагруженном орграфе имеются замкнутые пути отрицательной длины, то для заданных вершин v и w орграфа G, где v≠w, минимального пути из v в w может не быть. (Проанализировать самостоятельно.)
Таким образом, имеет смысл лишь задача поиска минимальных путей (маршрутов), среди путей (маршрутов), число дуг (ребер) в которых ограничено сверху.
Итак, рассмотрим задачу поиска минимального пути в нагруженном орграфе G (для нагруженного неорграфа рассуждения аналогичные ).
Пусть G=(V, E) – нагруженный орграф, V={v1, v2, …, vn}, n³2.
Обозначим 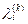 – длину минимального пути из v1 в vi, содержащего не более k дуг. Если таких путей нет, то
– длину минимального пути из v1 в vi, содержащего не более k дуг. Если таких путей нет, то 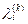 =¥. Кроме того, если каждый vi Î V считать путем из vi в vi нулевой длины, то
=¥. Кроме того, если каждый vi Î V считать путем из vi в vi нулевой длины, то 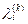 можно ввести и для k=0:
можно ввести и для k=0: 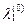 =0,
=0, 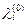 =¥ для i=2, …, n.
=¥ для i=2, …, n.
Опр.Матрицей длин дуг нагруженного орграфа G называется квадратная матрица D порядка n, в которой
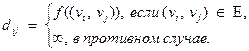
Значения 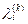 легко вычислить по формулам:
легко вычислить по формулам:
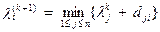 , i=2, …, n, k³0;
, i=2, …, n, k³0;
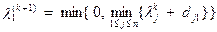 .
.
Результат оформляется в виде таблицы, где значение 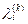 размещается в i-ой строке и k+1 столбце.
размещается в i-ой строке и k+1 столбце.
Алгоритм (Форда-Беллмана) нахождения минимального пути в нагруженном орграфе G из вершины v1 в вершину vi1 (i1≠1)(на примере)
Найдите минимальный путь в графе из вершины v1 в остальные вершины, если:
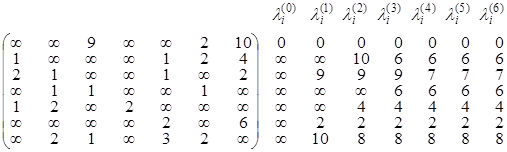
Найдем, к примеру, минимальный (v1, v2)-путь:
значение 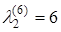 , значит, искомый путь существует и его длина равна 6. Наименьшее значение k, при котором
, значит, искомый путь существует и его длина равна 6. Наименьшее значение k, при котором 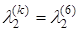 , равно 3, значит, в минимальном пути три дуги. Восстановление вершин дает значения (в обратном порядке) v5, v6. Таким образом, минимальный (v1, v2)-путь имеет вид v1®v6® v5® v2.
, равно 3, значит, в минимальном пути три дуги. Восстановление вершин дает значения (в обратном порядке) v5, v6. Таким образом, минимальный (v1, v2)-путь имеет вид v1®v6® v5® v2.
Определите, имеются ли в нагруженном орграфе G с заданной матрицей длин дуг DG, простые контуры отрицательной длины? Найдите пути минимальной длины из v1 во все остальные вершины среди путей, содержащих не более k дуг.
б) DG= 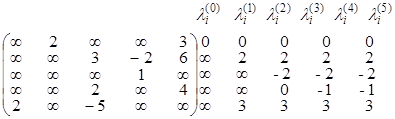 , k=4
, k=4
Алгоритм Дейкстры (применим к графам с неотрицательными длинами дуг)
Найдите длины минимальных путей (расстояния) в графе из вершины v1 в остальные вершины, если: