Определение коэффициента излучения и степени черноты тела
4.1. Цель работы
1. Закрепление знаний по тепловому излучению.
2. Ознакомление с методикой проведения экспериментов по определению степени черноты тела.
3. Развитие навыков проведения экспериментов.
4.2. Задание
1. Определить степень черноты e и коэффициент излучения поверхностей 2-х различных материалов (меди и алюминия).
2. Установить зависимость изменения степени черноты от температуры поверхности.
3. Сравнить значение степени черноты меди и алюминия между собой и со справочными данными.
4.3. Краткое теоретическое введение
Тепловое излучение представляет собой процесс переноса тепловой энергии посредством электромагнитных волн. Количество тепла, передаваемого излучением, зависит от свойства излучающего тела и его температуры и не зависит от температуры окружающих тел.
В общем случае тепловой поток, попадающий на тело, частично поглощается, частично отражается и частично проходит сквозь тело (рис. 2).
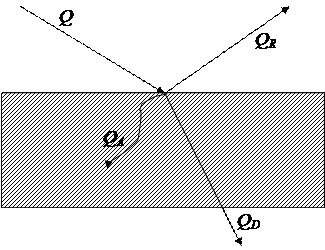
Рис. 2. Схема распределения лучистой энергии
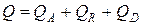 ,
,
где Q – тепловой поток, падающий на тело; QA – количество тепла, поглощаемое телом; QR – количество тепла, отражаемое телом; QD – количество тепла, проходящего сквозь тело.
Делим правую и левую части на тепловой поток:
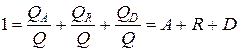 .
.
Величины A, R, D, называются соответственно: поглощательной, отражательной и пропускательной способностью тела.
Если R = D = 0, то A = 1, т.е. весь тепловой поток, падающий на тело, поглощается. Такое тело называется абсолютно чёрным.
Тела, у которых A = D = 0, R = 1, т.е. весь тепловой поток, падающий на тело, отражается от него, называются белыми. При этом если отражение от поверхности подчиняется законам оптики, тела называют зеркальными, если отражение диффузное – абсолютно белыми.
Тела, у которых A = R = 0 и D = 1, т.е. весь поток, падающий на тело, проходит сквозь него, называются диатермичными или абсолютно прозрачными.
Абсолютных тел в природе не существует, однако понятие о таких телах очень полезно, особенно об абсолютно чёрном теле, так как законы, управляющие его излучением, особенно просты, потому что никакое излучение не отражается от его поверхности.
Кроме того, понятие абсолютно чёрного тела даёт возможность доказать, что в природе не существует таких тел, которые излучают больше тепла, чем чёрные. Например, в соответствии с законом Кирхгофа отношение излучательной способности тела Е и его поглощательной способности А одинаково для всех тел и зависит только от температуры, для всех тел, включая и абсолютно чёрное, при данной температуре:
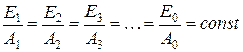 . (7)
. (7)
Так как поглощательная способность абсолютно чёрного тела A0 = 1, а A1 и A2 и т.д. всегда меньше 1, то из закона Кирхгофа следует, что предельной излучательной способностью E0 обладает абсолютно чёрное тело. Поскольку в природе абсолютно чёрных тел нет, вводится понятие серого тела, его степени черноты e, представляющее собой отношение излучательной способности серого и абсолютно чёрного тела:
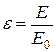 .
.
Следуя закону Кирхгофа и учитывая, что A0 = 1, можно записать 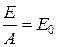 , откуда A = e, т.е. степень черноты характеризует как относительную излучательную, так и поглощательную способность тела. Основным законом излучения, отражающего зависимость интенсивности излучения E0, отнесённую к этому диапазону длин волн (монохроматическое излучение), является закон Планка.
, откуда A = e, т.е. степень черноты характеризует как относительную излучательную, так и поглощательную способность тела. Основным законом излучения, отражающего зависимость интенсивности излучения E0, отнесённую к этому диапазону длин волн (монохроматическое излучение), является закон Планка.
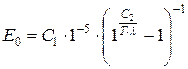 ,
,
где l – длина волн, м; С1 = 3,74×10–6 вт×м2, С2 = 1,4338×10–2 м×K; C1 и С2 – первая и вторая постоянные Планка.
На рис. 3 это уравнение представлено графически.
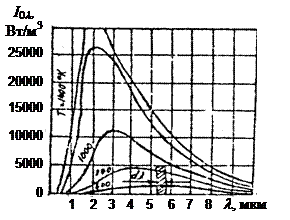
Рис. 3. Графическое представление закона Планка
Как видно из графика, абсолютно чёрное тело излучает при любой температуре в широком диапазоне длин волн. С возрастанием температуры максимум интенсивности излучения смещается в сторону более коротких волн. Это явление описывается законом Вина:
lmax×T = 2,898×10–3 м×K,
где lmax – длина волны, соответствующая максимуму интенсивности излучения.
При значениях l×T >> С2 вместо закона Планка можно применять закон Релея-Джинса, который носит кроме того название «закон длинноволнового излучения»:
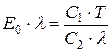 . (8)
. (8)
Интенсивность излучения, отнесённая ко всему интервалу длин волн от l = 0 до l = ¥ (интегральное излучение), можно определить из закона Планка путем интегрирования:
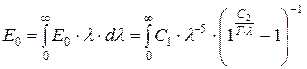 ,
,
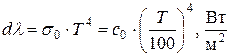 (9)
(9)
где С0 = 5,67 Вт/(м2×K4) – коэффициент излучения абсолютно чёрного тела. Выражение (9) носит название закона Стефана-Больцмана, который был установлен Больцманом. Для серых тел закон Стефана-Больцмана записывают в виде
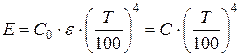 . (10)
. (10)
С = С0×e – излучательная способность серого тела. Теплообмен излучением между двумя поверхностями определяется на основании закона Стефана-Больцмана и имеет вид
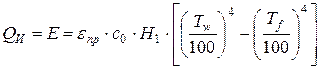 , (11)
, (11)
где eпр – приведённая степень черноты двух тел с поверхностями Н1 и Н2;
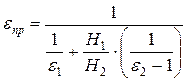 . (12)
. (12)
Если Н1 << Н2 то приведённая степень черноты становится равной степени черноты поверхности Н1, т.е. eпр = e1. Это обстоятельство положено в основу метода определения излучательной способности и степени черноты серых тел, имеющих незначительные размеры по сравнению с телами, обменивающимися между собой лучистой энергией
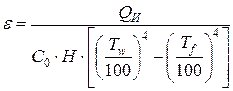 . (13)
. (13)
Как видно из формулы (13), для определения степени черноты и излучательной способности С серого тела необходимо знать температуру поверхности Tw испытуемого тела, температуру Tf окружающей среды и лучистый тепловой поток с поверхности тела QИ. Температуры Tw и Tf могут быть замерены известными способами, а лучистый тепловой поток определяется из следующих соображений.
Распространение тепла с поверхности тел в окружающее пространство происходит посредством излучения и теплоотдачи при свободной конвекции. Полный поток Q с поверхности, тела, таким образом, будет равен:
Q = QИ + QК, откуда QИ = Q – QK; (14)
где QK – конвективная составляющая теплового потока, которая может быть определена по закону Ньютона:
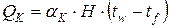 . (15)
. (15)
В свою очередь, коэффициент теплоотдачи aК может быть определён из выражения (см. работу № 3):
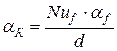 , (16)
, (16)
где 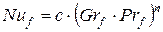 . (17)
. (17)
Определяющей температурой в этих выражениях является температура окружающей среды tf.
4.4. Схема экспериментальной установки
Экспериментальная установка, принципиальная схема которой изображена на рис. 4, предназначена для определения степени черноты двух материалов – меди и алюминия. Исследуемые тела представляют собой медную (9) и алюминиевую (10) трубки (элементы № 1 и № 2) с внутренним диаметром d1 = 18 мм, наружным диаметром d2 = 20 мм и длиной L = 460 мм, расположенные горизонтально. Внутри трубок размещены электронагреватели (11) из нихромовой проволоки, служащие источником тепла. Тепловой поток распределяется равномерно по длине трубы. При стационарном режиме всё тепло, выделяемое электронагревателем, передаётся через поверхность трубы в окружающую среду. Полная теплоотдача Q с поверхности трубы определяется по расходу электроэнергии. Потребляемая мощность электроэнергии регулируется автотрансформатором и измеряется амперметром и вольтметром или ваттметром.
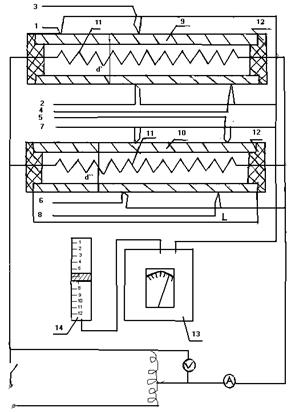
Рис. 4. Схема экспериментальной установки
Для уменьшения потерь тепла с торцов трубок располагают теплоизолирующие заглушки (12). Для измерения температуры поверхности в стенках каждой из трубок заложено по 5 медь-константовых термопар (№№ 1-5 первая труба и №№ 7-11 вторая труба). Термопары поочерёдно подключаются к измерительному прибору (13) при помощи переключателя (14).
4.5. Порядок проведения опытов и обработка результатов
Прежде чем приступить к выполнению лабораторной работы, необходимо ознакомиться с теоретическим материалом и устройством установки. Работа проводится на трёх режимах.
Таблица 2
Журнал наблюдений к работам № 2, 3, 4
| Режим 1 | |||||
| Элемент 1 | Элемент 2 | ||||
| Замер 1 | Замер 2 | Замер 1 | Замер 2 | ||
| Напряжение на нагревателе U, В | |||||
| Сила тока на нагревателе I, А | |||||
Тепловой поток 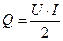 , Вт , Вт | |||||
| Темпера-туры на поверх-ности труб | Номера термопар | ||||
| Эл. 1 | Эл. 2 | ||||
| Среднее значение температуры tw, °С | |||||
| Температура воздуха (показания ДТВ) tf, °С |
После снятия замеров на 1-ом режиме необходимо показать преподавателю журнал наблюдений, после чего установить 2-ой тепловой режим. Установившийся тепловой режим наступает приблизительно через 3-5 мин. при выполнении работы на ПЭВМ.
На каждом из режимов необходимо произвести с интервалом 2‑3 мин. не менее 2-х замеров температуры на каждой из термопар и мощности по показаниям вольтметра и амперметра. Данные замеров занести в журнал наблюдений – табл. 2. Замеры производить только на установившемся режиме. Результаты расчётов свести в табл. 3. По полученным данным построить графики e = f(t) для 2-х испытуемых материалов. Полученные данные сравнить со справочными (табл. 7 приложения).
Физические параметры воздуха берутся из табл. 9 приложения при определяющей температуре tf .
Расчёт работы ведётся по табл. 3.
Таблица 3
Расчётная таблица к работе № 2
| № п/п | Наименование величины | Расчётные соотношения | Режим 1 | |
| Элемент 1 | Элемент 2 | |||
| Критерий Грасгофа | 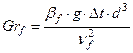 | |||
| a | Коэффициент объёмного расширения | 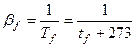 | ||
| b | Температурный напор | 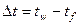 | ||
| c | Коэффициент кинематической вязкости воздуха | nf, м2/сек | ||
| Критерий Нуссельта | 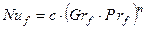 | |||
| а | Критерий Прандтля | Prf | ||
| b | Произведение (Grf ×Prf) | – | ||
| с | Коэффициенты, выбираются из табл. 5. (см. работу № 3) | c | ||
| n | ||||
| Поверхность трубы | 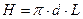 | |||
| Коэффициент теплоотдачи | 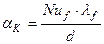 | |||
| а | Коэффициент теплопроводности воздуха | lf | ||
| Конвективная составляющая теплового потока | 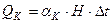 | |||
| Величина лучистого теплового потока | 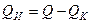 | |||
| Степень черноты | 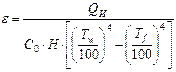 | |||
| Коэффициент излучения | 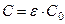 | |||
| Среднее значение степени черноты | 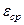 |
4.6. Содержание отчёта
1. Журнал наблюдений.
2. Обработка результатов опыта.
3. Сопоставление полученных данных между собой и со справочными данными.
4. Построение графика e = f(t) для исследуемых материалов.
4.7. Вопросы для самостоятельной проработки
1. Какова природа теплового излучения? От каких факторов зависит излучение тел?
2. Что такое селективный спектр и монохроматическое излучение?
3. Дайте определение абсолютно черного и серого тел, поглощательной способности степени черноты. Докажите, что коэффициент поглощения серого тела равен степени его черноты.
4.8. Защита работы
Для защиты работы необходимо ответить на 10 вопросов по теме «Тепловое излучение» (см. раздел «Контрольные вопросы к лабораторным работам»).
ПРИЛОЖЕНИЯ
Таблица 7
Степень черноты полного излучения различных материалов
| Материалы и характер поверхности | t, °С | e |
| Алюминий полированный | 225 – 575 | 0,039 – 0,067 |
| Алюминий шероховатый | 0,055 | |
| Алюминий, окисленный при 600°С | 200 – 600 | 0,11 – 0,19 |
| Дюралюминий окисленный | 50 – 150 | 0,36 – 0,37 |
| Дюралюминий полированный | 50 – 150 | 0,061 – 0,062 |
| Железо окисленное гладкое | 125 – 525 | 0,78 – 0,82 |
| Латунь полированная | 245 – 355 | 0,028 – 0,031 |
| Латунь тусклая | 50 – 350 | 0,22 |
| Медь полированная | 0,023 | |
| Медь, окисленная при нагреве до 600°С | 200 – 600 | 0,57 – 0,55 |
| Медь, окисленная при 300°С | 50 – 200 | 0,2 – 0,4 |
| Серебро полированное | 225 – 625 | 0,02 – 0,603 |
| Штукатурка известковая | 10 – 90 | 0,91 |
| Бумага | 0,8 – 0,9 | |
| Сажа ламповая | 40 – 370 | 0,95 |
| Снег | – | 0,96 |
| Масляные краски | 0,92 – 0,96 |
Таблица 8
Приведённые степени черноты
| Материалы трубы | Приведённая степень черноты |
| Алюминий | 0,10 – 0,13 |
| Медь | 0,23 – 0,26 |
Таблица 9
Физические свойства сухого воздуха
| t, °С | l, Вт/(м×град) | n×106 м2/с | Pr |
| 0,0244 | 13,28 | 0,707 | |
| 0,0251 | 14,16 | 0,705 | |
| 0,0259 | 15,06 | 0,703 | |
| 0,0267 | 16,00 | 0,701 | |
| 0,0276 | 16,96 | 0,699 | |
| 0,0283 | 17,25 | 0,699 | |
| 0,0290 | 18,97 | 0,696 | |
| 0,0296 | 10,02 | 0,694 | |
| 0,0305 | 21,09 | 0,692 | |
| 0,0313 | 22,10 | 0,690 | |
| 0,3210 | 23,13 | 0,682 | |
| 0,3340 | 24,65 | 0,686 |
8. Контрольные вопросы (тесты) к лабораторным работам
Теплопроводность
8.1.1. Теплопроводность – это процесс переноса теплоты (обмен внутренней энергией):
1. От тела к телу.
2. Внутри тела.
3. В металлах и диэлектриках.
4. Структурными частицами вещества – молекулами, атомами, электронами в сплошной среде при наличии градиента температур.
8.1.2. В каких телах процесс теплопроводности обусловлен диффузией молекул и атомов?
1. В жидкостях.
2. В металлах.
3. В газах.
4. В диэлектриках.
8.1.3. Как передаётся теплота внутри твёрдого тела?
1. Теплопроводностью.
2. Конвекцией.
3. Совместно конвекцией и теплопроводностью.
4. Совместно теплопроводностью и излучением.
8.1.4. Укажите размерность коэффициента теплопроводности:
1. 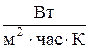 . 2.
. 2. 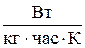 .
.
3. 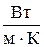 . 4.
. 4. 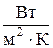 .
.
8.1.5. Укажите математическое выражение общего вида температурного поля:
1. t = f(x, c, r, l, t). 2. t = f(x, y, a, t).
3. t = f(x, y, z, a). 4. t = f(x, y, z, t).
8.1.6. Укажите закон Фурье:
1. 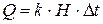 . 2.
. 2. 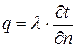 .
.
3. 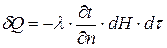 . 4.
. 4. 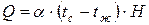 .
.
8.1.7. Укажите размерность плотности теплового потока:
1. 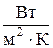 . 2.
. 2. 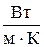 .
.
3. 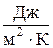 . 4.
. 4. 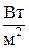 .
.
8.1.8. Количество теплоты, передаваемое через плоскую однослойную стенку:
1. 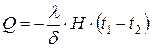 . 2.
. 2. 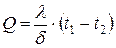 .
.
3. 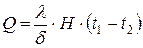 . 4.
. 4. 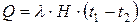 .
.
8.1.9. Укажите уравнение Лапласа:
1. 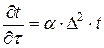 2.
2. 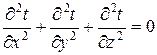
3. 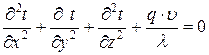 4.
4. 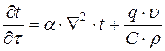
8.1.10. Какая поверхность называется изотермической?
1. Поверхность с одинаковым grad t.
2. Поверхность, во всех точках которой температура одинакова.
3. Поверхность, на которой 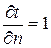 .
.
4. Поверхность, во всех точках которой давление одинаково.
8.1.11. Что называется температурным полем?
1. Значение температур в разное время.
2. Совокупность температур (её значений) во всех точках изучаемого пространства для каждого момента времени.
3. Значения температур тела.
4. Совокупность температур (её значений) во всех точках тела.
8.1.12. Укажите математическое выражение двухмерного нестационарного температурного поля:
1. t = ƒ(x, y, t). 2. t = f(x, y, z, t).
3. t = f(x, t). 4. t = f(x, y).
8.1.13. В каких телах процесс теплопроводности осуществляется за счёт свободных электронов?
1. В металлах.
2. В жидкостях.
3. В газах.
4. В диэлектриках.
8.1.14. Укажите размерность теплового потока Q:
1. Дж/с.
2. Вт/м.
3. ккал/(с×м2).
4. Дж/(м2×с).
8.1.15. Как изменяется удельный тепловой поток цилиндрической стенки?
1. Не изменяется в зависимости от радиуса.
2. Увеличивается с увеличением радиуса.
3. Уменьшается с увеличением радиуса.
4. Уменьшается с уменьшением радиуса.
8.1.16. Укажите граничные условия первого рода:
1. qn = q(x, y, z, t) 2. tc = t(x, y, z, t)
3. 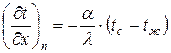 4.
4. 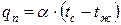
8.1.17. Что характеризует собой коэффициент теплопроводности l?
1. Интенсивность теплообмена между поверхностью тела и окружающей средой.
2. Способность вещества проводить теплоту.
3. Является мерой теплоинерционных свойств тела.
4. Все ответы правильные.
8.1.18. Укажите математическое выражение двухмерного стационарного температурного поля:
1. t = f(x, t). 2. t = f(x).
3. t = f(y, t). 4. t = f(y, x).
8.1.19. Укажите размерность коэффициента температуропровод-ности:
1. м/(°С×с). 2. м/с.
3. м2/с. 4. м/(кг×с).
8.1.20. Укажите дифференциальное уравнение для стационарной теплопроводности с внутренним источником тепла:
1. 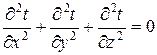 2.
2. 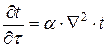
3. 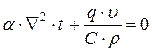 4.
4. 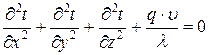
8.1.21. В каких телах процесс теплопроводности обусловлен распространением упругих волн?
1. В вакууме.
2. В металлах.
3. В газах.
4. В жидкостях и твердых телах – диэлектриках.
8.1.22. В основу вывода дифференциального уравнения теплопроводности положен:
1. Второй закон термодинамики.
2. Первый закон.
3. Закон Фурье.
4. Закон сохранения энергии и закон Фурье.
