БИЛЕТ 21. Повторение испытаний. Формула Бернулли
Пусть проводится n независимых испытаний, в каждом из которых событие A может появиться с вероятностью p и не появиться с вероятностью q = 1 - p. Обычно первый из двух возможных исходов называют удачей, а второй — неудачей. Поставим задачу выяснить вероятность того, что за n испытаний произошло ровно k удач, неважно, в какой последовательности (естественно, что всегда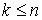 
).При заданной последовательности удач и неудач вероятность равна 
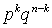(испытания независимы). Число различных способов, какими могут быть расположены k удач из n испытаний всего по формулам комбинаторики равно 
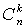. По формуле длявероятности суммы несовместных событий для вероятности ровно k удач из n испытаний всего, получаем (формула Бернулли): 
.
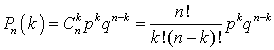Формула Бернулли применима для числа испытаний n<10, так как иначе получается большая ошибка. При n≥10 применяют теоремы Лапласа.
БИЛЕТ 22. Локальная и дифференциальная теоремы Лапласа
Дифференциальная(локальная): Пусть в каждом из n независимых испытаний событие А может наступить с вероятностью p прин. (0;1), тогда вероятность того, что событие А наступит ровно k раз в n испытаниях вычисляется по формуле Pnk=1/корень из npq*φ(x), где φ(x)=1/корень из 2пи*e-x2/2-дифференциальная функция Лапласа, значения которой приведены в таблицах для всех х<4.
φ(x)-четная, то есть φ(-x)= φ(x)
х=k-np/корень из npq
Интегральная: Пусть в каждом из n независимых испытаний событие А может наступить с вероятностью р прин. (0;1). Вероятность наступления А от k1 до k2 раз из n примерно равна:
Pn(k1;k2)=Φ(x’’)-Φ(x’)
x’=k1-np/корень из npq
x’’=k2-np/корень из npq
Φ(x)=1/корень из 2пи*интеграл от 0 до х от e-xdx – интегральная функция Лапласа, нечетная, то есть Φ(-x)= -Φ(x). В таблицах даны значения для всех x>5, в остальных случаях значение функции принимают равным 0,5
БИЛЕТ 23. Случайные величины. Закон распределения дискретной случайной величины
Случайной величиной называют величину, которая при данном испытании может принимать некоторые значения с некоторой вероятностью. Обозначается X,Y,Z, значения обозначают x1,x2,x3…
Если P(X=x1)=p1, P(X=x2)=p2…, то случайную величину можно записать в таблицу….Такая таблица называется ряд распределения случайной величины.
Случайная величина может быть двух типов: дискретная, принимающая отдельные изолированные значения и непрерывная, принимающая все значения некоторого интервала.
Для дискретной случайной величины составляют ряд(закон) распределения, то есть соответствие между значениями случайной величины и их вероятностями, записываемый обычно в таблицу.