БИЛЕТ 35. Проверка гипотез

Статистическая гипотеза — предположение о виде распределения и свойствах случайной величины, которое можно подтвердить или опровергнуть применением статистических методов к данным выборки

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина 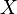, распределение которой полностью или частично неизвестно. Тогда любое утверждение, относительно называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение 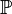, то есть 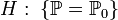, где 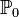какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения 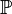к некоторому семейству распределений, то есть вида 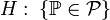, где 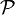— семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу 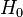. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза 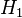, называемая конкурирующей или альтернативной.

Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.

В большинстве случаев статистические критерии основаны на случайной выборке 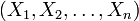фиксированного объема 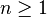для распределения 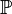. Впоследовательном анализе

выборка формируется в ходе самого эксперимента и потому её размер является случайной величиной (см. Последовательный статистический критерий).

Этапы проверки статистических гипотез

1. Формулировка основной гипотезы 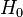и конкурирующей гипотезы .
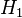2. Задание уровня значимости 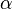, на котором в дальнейшем и будет сделан вывод о справедливости гипотезы. Он равен вероятности допустить ошибку первого рода.
3. Расчёт статистики 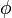критерия такой, что:
• её величина зависит от исходной выборки ;
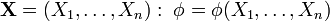• по её значению можно делать выводы об истинности гипотезы ;
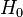• статистика 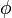, как функция случайной величины 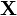, также является случайной величиной и подчиняться какому-то закону распределения.
4. Построение критической области. Из области значений 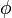выделяется подмножество 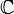таких значений, по которым можно судить о существенных расхождениях с предположением. Его размер выбирается таким образом, чтобы выполнялось равенство 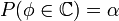. Это множество 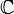и называется критической областью.
5. Вывод об истинности гипотезы. Наблюдаемые значения выборки подставляются в статистику 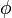и по попаданию (или непопаданию) в критическую область 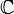выносится решение об отвержении (или принятии) выдвинутой гипотезы .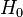