Законы Кирхгофа в операторной форме

Вопрос1

Характеристическое уравнение. Объяснить его физический смысл, роль начальных условий и законов коммутации.

Бессонов с 227-237 п8.2-8.13 (все жестко)

Характеристическое уравнение можно составить различными методами.

Δ=0 характеристическое уравнение где Δ(дельта)-определитель системы уравнений относительно свободных токов, число уравнений равно количеству неизвестных свободных токов.

Метод составления: (мб они и не нужны но все же)

· Первый метод – классический, когда характеристическое уравнение составляется строго в соответствии с дифференциальным по классической схеме. При расчете переходных процессов в сложной схеме составляется система из “m” дифференциальных уравнений по законам Кирхгофа для схемы цепи после коммутации. Так как корни характеристического уравнения являются общими для всех переменных, то решение системы дифференциальных уравнений выполняется относительно любой переменной (по выбору). В результате решения получают неоднородное дифференциальное уравнение с одной переменной. Составляют характеристическое уравнение в соответствии с полученным дифференциальным и определяют его корни.

· Метод входного сопротивления
1)составить эквивалентную схему без источников
2)разомкнуть любую соединительную линию
3)относительно полученных зажимов (при размыкание) найти входное сопротивление электрической цепи
4)прировнять к нулю

· Метод определителей матриц коэффициентов :

1)описать эквивалентную операторную схему любым способом

(как правило методом контурных токов)

2)записать уравнение в матричном виде

3) прировнять lAl=0 (определитель к нулю)

Независимые начальные условия (законы коммутации )
1)iL(0-)=iL(0+)

2)Uc(0-)=Uc(0+)

Зависимые начальные условия все остальные U(0+) и i(0+)

относительно независимых начальных условий находятся зависимые начальные условия по уравнениям Кирхгофа.

Так же читайте 2ой вопрос

Вопрос2

Дать краткое определение характеристического уравнения. Раскрыть принцип нахождения коэффициентов в функции переходного процесса для первого порядка цепи (коэффициенты А и остальные параметры, если есть).

Δ=0 характеристическое уравнение где Δ(дельта)-определитель системы уравнений относительно свободных токов, число уравнений равно количеству неизвестных свободных токов.

Составленное по 2ому закону Кирхгофа уравнение :
UL+r*i=E эквивалентно L*(di/dt)+r*i=E

Решение i=iпр(принужденное )+iсв(свободное)

Частное решение = E/R (iпр)

Общим решением этого уравнение является показательная функция следующего вида: A*e^(p*t)

iсв (i свободное ) = A*e^(p*t)

L*(diсв/dt)+r*iсв=0 (приравниваем правую часть к нулю для нахождения свободных токов)

постоянная интегрирования(коэффициент амплитуды) А для каждого свободного тока своя.

а коэффициент затухания(корень характеристического уравнения) р одинаков для свободных токов ветвей
А и р не зависят от времени
А= -(E/r)

P= - (L/r)

Следовательно

i=iпр(принужденное )+iсв(свободное)
i=E/r-(E/r)*e^(-(r/L)*t)

ссылка на лекцию https://pp.vk.me/c630426/v630426043/ef48/_JJArujBZiQ.jpg

так же не плохой сайт http://ruseti.ru/magnit/katushka101.html

Вопрос3

Законы Кирхгофа в операторной форме.

Справочник:

Формула(не рисунок)14-1: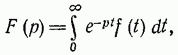

Формула(не рисунок)14-(4-5):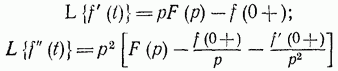

Формула(не рисунок)14-7: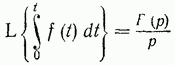

-------------------------------------------------------------------------------------------------------------------------

Законы Кирхгофа в операторной форме:

Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю.

.

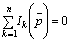Второй закон Кирхгофа: алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура.

.

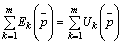Подробности:

Для любого узла разветвленной цепи

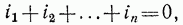
поэтому, обозначив изображения токов Ik(p)=ik(t) на основании (14-1) получим первый закон Кирхгофа в операторной

форме,

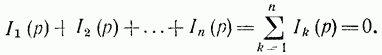(14-20)

для любого замкнутого контура, состоящего из n ветвей,

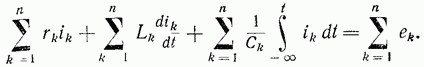
Полагая

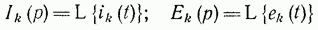
и повторяя все рассуждения, которые были сделаны при записи закона Ома в операторной форме, получаем второй закон Кирхгофа в операторной форме:

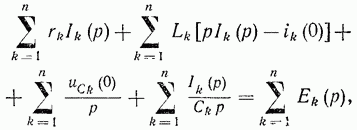
что можно переписать так:

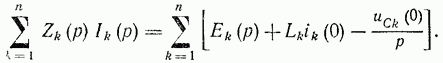(14-21)

В последних выражениях ik(0) и Uck(0) — начальные значения токов в катушках индуктивности и напряжений на конденсаторах в соответствующих ветвях.

Особенно просто запишется второй закон Кирхгофа при нулевых начальных условиях, т. е. при ik(0)=0и Uck(0)=0

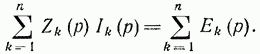(14-22)

В такой записи он полностью аналогичен второму закону Кирхгофа в комплексной форме.

вопрос4

Магнитные цепи. Основные понятия: намагниченность, магнитная индукция, напряженность, магнитный поток, абсолютная и относительная магнитные проницаемости. петля гистерезиса и ее характеристики

Магнитная цепь — последовательность взаимосвязанных магнетиков, по которым проходит магнитный поток. При расчётах магнитных цепей используется почти полная формальная аналогия с электрическими цепями. В схожем математическом аппарате также присутствует закон Ома, правила Кирхгофа и другие термины и закономерности.

Намагни́ченность, характеристика магнитного состояния макроскопического физического тела. Любое вещество, помещенное в магнитное поле, приобретает некоторый магнитный момент. Намагниченность– это магнитный момент единицы объема. В случае однородно намагниченного тела намагниченность определяется как:

J = M/V

где М — магнитный момент тела, V — его объем.

В несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничивание: J =H, где — магнитная восприимчивость вещества.

В случае неоднородно намагниченного тела намагниченность определяется для каждого физически малого объема dV:

J = dM/dV,

где dM — магнитный момент объема dV.

Единица намагниченности в Международной системе единиц — ампер на метр (1 А/м — это такая намагниченность, при которой 1 м³ вещества обладает магнитным моментом 1 Ахм²).

Намагниченность тел зависит от внешнего магнитного поля и температуры.

У ферромагнетиков зависимость J от напряженности внешнего поля Н выражается кривой намагничивания. В изотропных веществах направление J совпадает с направлением Н, в анизотропныхнаправления J и Н в общем случае не совпадают.

МАГНИТНАЯ ИНДУКЦИЯ

-векторная физическая величина, характеризующая магнитное поле.

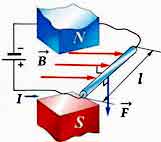
Вектор магнитной индукции всегда направлен по касательной к магнитной линии

Расчетная формула:

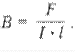
где F- сила, действующая со стороны магнитного поля на проводник с током ( H );
I - сила тока в проводнике ( A );
l - длина проводника ( м ).

Единица измерения индукции магнитного поля в СИ:
[ B ] = 1Тл ( тесла).

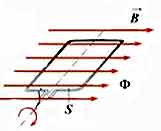
МАГНИТНЫЙ ПОТОК

Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком
( потоком векторов магнитной индукции).

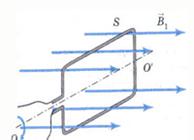
Ф - магнитный поток, пронизывающий площадь контура, зависит от
величины вектора магнитной индукции, площади контура и его ориентации относительно линий индукции магнитного поля.

Если вектор магнитной индукции перпендикулярен площади контура, то магнитный потокмаксимальный.

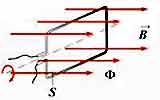
Если вектор магнитной индукции параллелен площади контура, то магнитный поток равен нулю.

Напряженностью магнитного поля называют векторную величину 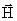, характеризующую магнитное поле и определяемую следующим образом:

,

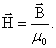Напряженность магнитного поля заряда q, движущегося в вакууме равна:

,

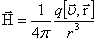Это выражение показывает закон Био–Савара–Лапласа для .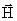

Напряженность магнитного поля 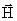является, как бы, аналогом вектора электрического смещения 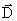в электростатике.

Абсолютная магнитная проницаемость среды описывает магнитные свойства среды. Абсолютная магнитная проницаемость среды обозначается μ_a.

Магнитная постоянная

Для описания магнитных свойств вакуума используют магнитную постоянную. Магнитная постоянная обозначается μ₀. Магнитная постоянная равна:

μ₀ = 4π * 10^-7 Гн/м

Гн - генри, генри равен Ом*с.

Относительная магнитная проницаемость среды

Относительная магнитная проницаемость среды описывает во сколько раз индукция данного магнитного поля в данной среде отличается от индуции этого же поля в вакууме. Относительная магнитная проницаемость среды обозначается μ_r или просто μ. Относительная магнитная проницаемость среды является безразмерной величиной. Относительная магнитная проницаемость для ферромагнитных материалов зависит от изменения магнитного поля. Для прочих материалов относительная магнитная проницаемость примерно равна единице и постоянна.

Формула абсолютной магнитной проницаемости

Формула абсолютной магнитной проницаемости:

μ_a = μ₀ * μ_r

Магнитный гистерезис Если предварительно размагниченный образец ферромагнитного материала подвергнуть намагничиванию до состояния технического насыщения, то с увеличением напряженности магнитного поля Н магнитная индукция образца В будет изменяться в соответствии с кривой ОАБ (рисунок 2.2). 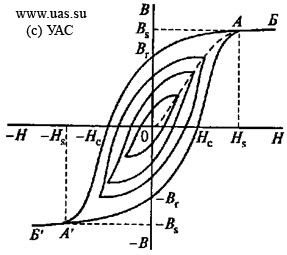Рисунок 2.2 – Предельная петля магнитного гистерезиса В точке А при H = Hs магнитная индукция образца достигнет индукции насыщения Bs. При уменьшении напряженности поля Н намагниченность образца уменьшается по кривой БАBr, и при Н = 0 образец будет обладать некоторой индукцией, величина которой будет отлична от нуля. Эта индукция называется остаточной и обозначается Вr. Остаточная индукция (остаточная намагниченность) обусловлена тем, что при размагничивании, когда Н = 0, магнитные моменты доменов оказываются ориентированными вдоль оси легкого намагничивания, направление которой близко к направлению внешнего. Для достижения полного размагничивания образца к нему необходимо приложить противоположное по знаку поле определенной напряженности. Напряженность такого поля называют коэрцитивной силой Нс. При дальнейшем усилении отрицательного поля магнитная индукция тоже становится отрицательной и в точке A' при H = –Hsдостигает значения индукции технического насыщения (B = –Bs). После уменьшения отрицательного поля, а затем увеличения положительного поля кривая перемагничивания опишет петлю, называемую предельной петлей магнитного гистерезиса, которая является важной технической характеристикой магнитных материалов. Таким образом, предельная петля магнитного гистерезиса – это кривая изменения магнитной индукции при изменении внешнего магнитного поля от +Hs до –Hs и обратно. Пользуясь предельной петлей магнитного гистерезиса можно определить основные параметры материала: коэрцитивную силу Нс, индукцию насыщения Bs, остаточную индукцию Br и др. Такие характеристики материала, как точка Кюри и индукция насыщения, зависят только от химического состава магнитных материалов. Коэрцитивная сил Нс, магнитная проницаемость M и площадь петли гистерезиса являются структурночувствительными. Чем больше размер зерна (меньше суммарная удельная поверхность зерен) и более совершенна структура кристаллической решетки (меньше дислокаций, внутренних напряжений, примесей и других дефектов), тем меньше Нс и больше M, а материал легче намагничивается и перемагничивается. По величине коэрцитивной силы магнитные материалы подразделяются намагнитомягкие и магнитотвердые. Материалы, у которых Нс< 4 кА/м, относятся к магнитомягким, у которых Нс > 4 кА/м – к магнитответдым (ГОСТ 19693 – 74). Для магнитомягких материалов характерно малое значение коэрцитивной силы. У промышленных образцов наименьшая Нс = 0,4 А/м. Поэтому они намагничиваются до индукции технического насыщения при невысоких напряженностях поля. У магнитомягких материалов высокая магнитная проницаемость, малые потери на перемагничивание и узкая петля гистерезиса при высоких значениях магнитной индукции. Для магнитотвердых материалов характерна широкая петля гистерезиса с большой коэрцитивной силой. У промышленных образцов наибольшая Нс = 800 кА/м. Магнитотвердые материалы намагничиваются при высокой напряженности внешнего магнитного поля, но зато длительное время сохраняют сообщенную энергию.

Вопрос5