Петербургская математическая школа

Становление российской математики

Еще со времен Киевской Руси восточно - славянские племена оживленно общались с другими народами, обменивались с ними знаниями и навыками. Уровень математических знаний Древней Руси был вполне сопоставим с уровнем знаний ее соседей. Наши предки умели выполнять арифметические действия с многозначными числами, вычислять площади земельных участков, умели и многое другое.

Реформы Петра I, при котором Московское царство преобразовалось в Российскую империю, способствовали еще более тесным связям России с Западной Европой. Потребности молодого государства требовали широкого использования научных знаний, и 24 января 1724 года Петр I подписал Указ об организации Академии наук, а при ней — университета и гимназии. В 1999 году Российской Академии наук и Санкт-Петербургскому университету исполнилось 275 лет.

Первые профессора молодой академии приглашались из-за границы; так, в 1727 году был приглашен Леонард Эйлер, который работал в Петербурге с 1727 года по 1741 год, а затем еще раз с 1766 по 1783 год.

Деятельность Эйлера в Академии наук и в университете была многообразна. Он выполнял многочисленные поручения правительства ― в области картографии России, артиллерии, оптики, публиковал как глубокие теоретические работы, так и учебники, воспитал ряд учеников, которые продолжали его дело ― правда, уже не на таком высочайшем уровне, как он.

В первой половине XIX века наиболее известными математиками России были академики Виктор Яковлевич Буняковский (1804―1889) и Михаил Васильевич Остроградский (1801―1861), опубликовавшие ряд первоклассных работ. Однако в Западной Европе к тому времени еще не привыкли со вниманием относиться к российской науке и следить за ее достижениями. Поэтому выдающиеся результаты российских ученых с опозданием усваивались мировым научным сообществом.

Так, знаменитое и широко используемое неравенство Буняковского

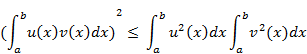
за рубежом связывают с именем Шварца (Schwarz K., 1843—1921), хотя Шварц открыл его только в 1875 году, на 16 лет позже публикации В. Я. Буняковского.

В 1834 году в изданиях Российской Академии наук была опубликована памятная записка ("мемуар") М. В. Остроградского, а через шесть лет, в 1840 году, Парижская Академия наук объявила конкурс на премию за решение той же самой, уже решенной Остроградским, проблемы. Лишь в 1861 году мемуар М. В. Остроградского в полном переводе на английский язык был издан как приложение к книге Тотгентера по истории вариационного исчисления (цитирую по книге Гнеденко Б. В. Очерки по истории математики в России. — М., Л.: ОГИЗ, 1946).

Мировое признание российской математики пришло после того, как во второй половине XIX века заявила о себе петербургская математическая школа, сформировавшаяся, прежде всего, вокруг великого русского математика Пафнутия Львовича Чебышёва (1821―1894).

Петербургская математическая школа

Чебышёв родился в 1821 году в старинной дворянской семье в Калужской губернии. Первоначальное образование он получил дома, затем с 1837 года учился в Московском университете, окончив его в 1841 году. В Москве, в 1846 году, Чебышёв защитил магистерскую диссертацию "Опыт элементарного изложения теории вероятностей", но уже в 1847 году переехал в Петербург, где был утвержден доцентом Петербургского университета и начал чтение лекций. В 1850 году он был избран экстраординарным, а в 1860 году ― ординарным профессором Петербургского университета, в котором он читал лекции 35 лет ― с 1847 по 1882 год. Одновременно П. Л. Чебышёв работал в Академии наук, куда он в 1853 году был избран адъюнктом, в 1858 году ― академиком, а также много и плодотворно работал в Артиллерийском комитете; таким образом ― и это весьма важно отметить ― П.Л. Чебышёв не был "исключительно преподавателем": с преподаванием он соединял и научную, и чисто практическую деятельность; это не могло не наложить отпечатка и на его преподавание в университете.

Первые выдающиеся работы П. Л. Чебышёва относились к наиболее отвлеченному отделу математики ― теории чисел. Этой теме была посвящена и его докторская диссертация "Теория сравнений" (1849), и знаменитая статья "Об определении числа простых чисел, не превосходящих заданной величины", опубликованная в 1851 году.

Однако постепенно научные интересы Чебышёва перемещаются в область механики. В 1852 году он получает заграничную командировку. Чебышёв использовал эту возможность для личного знакомства с выдающимися зарубежными математиками ― Коши, Лиувиллем, Эрмитом ― и, одновременно, он с величайшим интересом знакомился с передовой в те годы французской промышленностью, центральным звеном которой была паровая машина. "Из многих предметов исследования, ― писал П. Л. Чебышёв в своем отчете о заграничной командировке, ― которые представились мне при рассмотрении и сличении между собой различных механизмов передачи движения ― особенно в паровой машине, где и экономия в топливе, и прочность машины много зависят от способов передачи работы пара, я особенно занялся теорией механизмов, известных под названием параллелограммов". Шарнирные механизмы (в то время "параллелограммы") широко применялись тогда в паровых машинах. Задачей этих механизмов было обеспечение движения поршня, в наименьшей мере отклоняющегося от прямолинейного. В ходе исследования параллелограммов Чебышёв, по его собственным словам, "встретил вопросы анализа, о которых до сих пор знали очень мало". Это были вопросы о построении функций наилучшего приближения. Чебышёв глубоко разработал теорию подобных функций и, в частности, открыл знаменитые полиномы, в наименьшей степени уклоняющиеся от нуля, — полиномы вида:

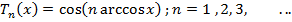
Эти полиномы в дальнейшем были названы полиномами Чебышёва и получили многообразные применения.

Таким образом, теоретические открытия Чебышёва вырастали из вопросов практики, на которые он горячо откликался. Этот путь ― от насущных практических задач к теоретическим обобщениям ― он считал наиболее плодотворным. Вот что говорил об этом сам Чебышёв в речи на торжественном акте Петербургского университета в 1856 году: "Науки математические с самой глубокой древности обращали на себя особенное внимание; в настоящее время они получили еще более интереса по влиянию своему на искусства и промышленность. Сближение теории с практикой дает самые благотворные результаты, и не одна только практика от этого выигрывает; сами науки развиваются под влиянием ее: практика открывает им новые предметы для исследования или новые стороны в предметах, давно известных".

И тут же в своей актовой речи (кстати, названной им "Черчение географических карт") Чебышёв дает пример этого благотворного взаимодействия конкретных задач практики и их теоретического обобщения. Чебышёв рассматривает одну из центральных задач картографии ― какая проекция является наиболее выгодной для создания карты конкретной страны ― и показывает, что задача эта не сводится к обычным задачам дифференциального или вариационного исчисления, но может быть решена на основе теории функций, наименее уклоняющихся от нуля, разработанной им ранее для задач о параллелограммах паровых машин. На основе этой теории Чебышёв дает решение как в общем виде (в форме принципа: "на границе изображения масштаб постоянен"), так и конкретное решение для карты Европейской части России, которое позволило снизить погрешность изображения с 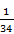(достигаемой при стереографической проекции) до .

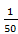Любопытно, что доказать строго свой принцип выбора наилучшей проекции ("на границе изображения масштаб постоянен") Чебышёву в то время не удалось, хотя он проверил его на примерах, был уверен в его правильности и широко им пользовался. Полное доказательство принципа Чебышёва было дано лишь 40 лет спустя, в 1896 году, русским математиком Дмитрием Александровичем Граве (1863―1939) в его докторской диссертации "Об основных задачах математической теории построения географических карт", защищенной В Петербургском университете уже после смерти П. Л. Чебышёва.

Мы рассмотрели только немногие из научных результатов П. Л. Чебышёва; всего с 1843 по 1894 год им опубликовано 69 работ, многие из которых получили мировую известность. (Любитель сравнений может заметить, что П. Л. Чебышёв опубликовал вдесятеро меньше работ, чем О. Коши, но это лишь еще раз подчеркивает, что дело не в количестве работ, а в их значимости.) Не меньшее значение имела и деятельность П. Л. Чебышёва в качестве профессора Петербургского университета. Вот что пишет о лекциях Чебышёва его ученик А. М. Ляпунов: "Курсы его не были обширными, и при изложении их он заботился не столько о количестве сообщаемого материала, сколько о выяснении принципиальных сторон трактуемых вопросов. Отличаясь живым и увлекательным изложением, лекции его сопровождались множеством интересных замечаний относительно значения и важности тех или других вопросов или научных методов. Замечания эти высказывались иногда мимоходом по поводу какого-нибудь конкретного случая, но всегда глубоко западали в умах его слушателей. Вследствие этого лекции его имели высокое развивающее значение, и слушатели его после каждой лекции выносили нечто существенно новое в смысле большей широты взглядов и новизны точек зрения.

П. Л. Чебышёв почти не пропускал лекций. По крайней мере, за два года, в течение которых я был его слушателем, я не помню, чтобы хотя один раз его лекция не состоялась. В аудитории он появлялся всегда точно в назначенное время и тотчас же, не теряя ни секунды, приступал к продолжению выводов, начатых в предшествовавшую лекцию. Вычисления он производил чрезвычайно быстро, вследствие чего, несмотря на то, что был прекрасным калькулятором, часто делал ошибки в выкладках, и за ходом вычислений нужно было следить очень внимательно, чтобы вовремя предупредить о сделанной ошибке, о чем он всегда просил своих слушателей. Когда, наконец, получался желаемый вывод, П. Л. Чебышёв садился в кресло, ставившееся для него всегда у первой парты, и вот тут-то и начинались те разнообразные замечания, которые придавали особый интерес его лекциям и которых с нетерпением ждала вся аудитория. Весьма часто по поводу только что решенного вопроса Чебышёв высказывал свое мнение о тех или других работах, относящихся к тому же вопросу. Иногда он вспоминал при этом некоторые эпизоды из своих заграничных поездок, рассказывал о беседах по поводу того же вопроса с кем-либо из иностранных ученых. После более или менее продолжительной беседы этого рода, служившей для него отдыхом, П. Л. Чебышёв, быстрый как в речи, так и во всех своих действиях, быстро вставал, брался за мел и приступал к дальнейшим выводам. К характеристике внешней стороны его лекций должно прибавить, что он никогда не оставался в аудитории по окончании времени, назначенного для лекции, и бросал мел в тот же момент, как раздавался звонок, на каком бы месте при этом ни пришлось оборвать начатые вычисления".

Заметим, что лекции П. Л. Чебышёва по вычислению определенных интегралов, теории конечных разностей и теории вероятностей, дословно записанные А. М. Ляпуновым, были изданы АН СССР в 1936 году, и желающие могут с ними ознакомиться. Наибольшей научной заслугой П. Л. Чебышёва А. М. Ляпунов справедливо считает создание школы математиков, известной как петербургская математическая школа, к которой принадлежали А. Н. Коркин, Е. И. Золотарев, А. А. Марков, К. А. Поссе, Д. А. Граве, В. А. Стеклов, Г. Ф. Вороной и, прежде всего, сам А. М. Ляпунов.

Отметим, что до известной степени к петербургской математической школе можно отнести и Софью Васильевну Ковалевскую (1850―1894). Хотя она училась в Германии, у К. Вейерштрасса, но, вернувшись в 1874 г. в Россию, в Петербург, она активно общалась с П. Л. Чебышёвым и его учениками. В 1889 году по предложению Чебышёва ее избрали членом-корреспондентом Академии наук. В тесном контакте и оживленном общении с петербургскими математиками она работала до своего отъезда в Швецию в 1883 году.

Вот как определяет А. М. Ляпунов основные черты петербургской школы: "П. Л. Чебышёв и его последователи остаются постоянно на реальной почве, руководясь взглядом, что только те изыскания имеют цену, которые вызываются приложениями (научными или практическими), и только те теории действительно полезны, которые вытекают из рассмотрения частных случаев.

Детальная разработка вопросов, особенно важных с точки зрения приложений и, в то же время, представляющих особенные теоретические трудности, требующие изобретения новых методов и восхождения к принципам науки, затем обобщение полученных выводов и создание этим путем более или менее общей теории ― таково направление большинства работ П. Л. Чебышёва и ученых, усвоивших его взгляды.

Насколько подобное направление может быть плодотворным в чисто научном отношении, это, вероятно, показывает вся научная деятельность П. Л. Чебышёва, который пришел к постановке и решению совершенно новых и важных вопросов анализа, исходя из задач прикладного характера, иногда притом чисто практических. Таков, впрочем, путь многих важных открытий в области математики", ― заканчивает А. М. Ляпунов.

Отметим теперь, что, несмотря на традиции петербургской математической школы, в начале XX века на физико-математическом факультете Петербургского университета (до 1919 года этот факультет объединял и физиков, и математиков) наблюдался крен в сторону математической абстракции, от которого страдали прежде всего физики объединенного факультета. Особенно тяжело приходилось молодым физикам, готовившимся к сдаче магистерских экзаменов. Математики объединенного факультета не хотели признавать, что человек, готовящийся к профессии физика, может (и должен) предъявлять к своему математическому образованию совсем другие требования, чем "чистый" математик, и экзаменовали молодых физиков "по всей строгости" своей науки. Это приводило ко многим трагедиям. В воспоминаниях о Павле Сигизмундовиче Эренфесте (1880―1933) приводился характерный эпизод — в 1912 году на Всероссийском съезде естествоиспытателей и врачей в Москве П. С. Эренфест с увлечением рассказывал о выдающемся научном открытии молодого тогда физика Д. С. Рождественского (1876―1940). Работа, действительно, была блестящей, и аудитория закидала П. С. Эренфеста вопросами: "А где же сам автор работы?" "Где?" ― со слезами на глазах переспрашивал П. С. Эренфест и отвечал: "Автор этого открытия, имеющего мировое значение, не имел времени приехать в Москву; он, не разгибая спины, готовится к магистерскому экзамену по математике. Чтобы сдать эти экзамены, надо прочесть вот какие книги". Эренфест подошел к доске и, волнуясь от негодования, начал выписывать длинную колонку книг, ознакомление с которыми требовалось программой экзаменов.

И это была, конечно же, участь не одного Рождественского. О сложившемся положении со стилем преподавания математики на физико-математическом факультете А. Ф. Иоффе говорил в 1910 году: "Это ― трагедия петербургской физики" (цитирую по книге Френкеля В. Я. Пауль Эренфест. — М., 1977).

И не удивительно, что когда в 1919 году из физико-математического факультета Петроградского университета был выделен факультет физический, и к организации его был привлечен Д. С. Рождественский, он прежде всего провел реформу преподавания математики, приведя ее в соответствие с действительными нуждами физики. Реформа встретила яростное сопротивление профессоров-математиков. "Университет будет теперь выпускать поверхностно образованных людей, ― утверждали они, ― вместо выпускников, приученных к математической строгости мышления". Д. С. Рождественский, по свидетельству мемуариста, "отвечал математикам резко, даже с оттенком презрительности, как людям, которые оторвались от жизни и не понимают ее требований" ("Воспоминания о Рождественском", изд-во "Наука", 1976).

Рождественский довел реформу до конца — новый курс математики, учитывающий нужды физиков, был составлен Владимиром Ивановичем Смирновым (1887―1974) совместно с Я. Д. Тамаркиным, который впоследствии эмигрировал, так что Смирнов продолжил работу уже один. Из этой работы вырос потом столь известный "Курс высшей математики" В. И. Смирнова в пяти томах. Популярность этого курса (переведенного на многие языки мира) определилась тем, что он излагал математические вопросы с точки зрения приложений и, прежде всего, приложений в физике. Деятельность петербургской математической школы наглядно показала, насколько плодотворным для математики может быть влияние приложений.

Представителем петербургской математической школы, с особенным успехом работавшим в области прикладной математики, был Алексей Николаевич Крылов (1863―1945).

А. Н. Крылов родился в 1863 году в небогатой дворянской семье, в 1878 году поступил в Морское училище, которое закончил в 1884 году, получив воинское звание мичмана. Еще в Морском училище, во многом под влиянием А. М. Ляпунова, своего двоюродного брата по матери, А. Н. Крылов начал глубоко интересоваться математикой, изучая самостоятельно университетские курсы. После окончания Морского училища А. Н. Крылова привлекли к работе по изучению девиации магнитного компаса и методам ее уничтожения. В 1888―1890 годах А. Н. Крылов учился в Морской академии, где курс математики вел Александр Николаевич Коркин (1837―1908) ― один из лучших представителей петербургской математической школы. По окончании академии А. Н. Крылов много лет преподавал в Морском училище и Морской академии, совмещая преподавание с большой практической работой. В разное время А. Н. Крылов работал заведующим судостроительным бассейном (с 1900 г.), главным инспектором кораблестроения (с 1908 г.), председателем Морского технического комитета (с 1908 г.), директором Главной физической обсерватории (с 1916 г.), начальником Морской академии (с 1919 г.), директором Физико-математического института Академии наук с 1927 года (действительным членом Академии наук А. Н. Крылов был избран еще в 1916 году).

Все эти практические работы А.Н. Крылова не могли не оказать влияния на направленность его математических трудов. А. Н. Крылов блестяще знал математику, но его работы почти исключительно были посвящены математике прикладной. А. Н. Крылов ― это классик прикладной математики.

Тематика работ А. Н. Крылова разнообразна: они посвящены теории и расчету качки корабля на морском волнении, теории показаний корабельных гиро- компасов и магнитных компасов, расчету напряжений и деформаций в элементах судовых конструкций и многим другим практическим задачам кораблестроения и мореходного дела. Какие же основные черты пронизывают все эти столь разнообразные труды А. Н. Крылова? Что позволяет считать эти труды классическими работами по прикладной математике? Отметим, прежде всего, что важнейшие работы А. Н. Крылова, будь это работы по исследованию качки судов, показаний компасов или других явлений, прежде всего включают в себя подробный выбор, анализ и обоснование принимаемой им математической модели исследуемого явления. Именно обоснование правильного выбора математической модели исследуемого объекта ― а это, в свою очередь, невозможно без хорошего знания физической сущности и практических особенностей работы объекта ― и составляет самую важную, решающую часть исследований А. Н. Крылова. Крылов рассматривает предлагаемую им математическую модель с двух в равной мере важных точек зрения: во-первых, математическая модель должна достаточно хорошо отражать хотя бы основные черты изучаемого явления ― для того, чтобы результаты расчета по математической модели достаточно хорошо совпадали с реальностью, а, во-вторых, математическая модель должна быть разрешимой, должна допускать конкретное, доведенное до конца решение, которое можно было бы сопоставить с экспериментом.

В выборе такой подходящей математической модели и заключается главная трудность работы прикладного математика, а в преодолении этой трудности и проявляется, прежде всего, его искусство. Действительно, бесчисленное количество плохих работ по прикладной математике отличается от работ хороших присутствием одного из двух решающих недостатков: либо избранная автором математическая модель не соответствует в должной мере реальному процессу, и поэтому все исследование бесполезно, либо избранная модель чрезмерно сложна и превышает возможности автора довести решение до конца. А. Н. Крылов умел избегать обоих этих недостатков, и поэтому изучение его работ является столь поучительным для всех, работающих в области прикладной математики, ― тем более, что работы эти доступны, они собраны в опубликованном Академией Наук СССР в 1948―1951 годах двенадцатитомном собрании его сочинений.

Еще одна характерная черта работ А. Н. Крылова, делающая его классиком прикладной математики, ― это доведение результатов до ясных, четких и понятных практических рекомендаций. "Чистые" математики часто ограничиваются формулировкой и доказательством теорем. В противоположность этому А. Н. Крылов при изложении своих результатов вообще не пользуется словом "теорема". Вместо этого он подробно и досконально объясняет читателю ― почему, на каких основаниях выбрал он математическую модель; каким образом следует проводить вычисления по этой модели для того, что-бы получить согласие между вычислением и реальной действительностью, какие практические трудности могут встретиться в вычислениях, и как лучше всего эти трудности преодолеть. Для работ прикладного характера такой способ изложения чрезвычайно важен.

В сочинениях А. Н. Крылова можно найти и его взгляды на преподавание прикладной математики, выраженные с присущей А. Н. Крылову яркостью и силой.

Во второй половине XIX века наметилось расхождение в стиле преподавания математики в университетах и в технических учебных заведениях. Вот что писал об этом А. Н. Крылов в 1916 г.: "В последние 30―40 лет большая часть первоначальных положений и определений математических понятий подвергалась обстоятельнейшей критике, приведшей, с одной стороны, к уточнению этих понятий и полной логической строгости выводов, но, с другой стороны, ― это уточнение привело к растянутости многих рассуждений, к утрате, так сказать, наглядной самоочевидности выводов.

В технической школе такая постановка преподавания противоречит самому духу школы, всей дальнейшей деятельности ее питомцев, самому ее назначению ― прежде всего вырабатывать сметку, глазомер, решимость, веру в чертеж и в свидетельства чувств, а не ту как бы умственную трусость, которая заставляет изыскивать доказательства таких истин, которые технику кажутся до доказательства яснее, чем после такового".

Очень интересно говорил А. Н. Крылов и относительно объема сведений по математике, который необходимо давать в технической школе. Вот отрывок из его вступительной лекции, прочитанной в 1932 году для слушателей, желающих повысить знания по математике в Военно-Морской Академии: "Я 45 лет занимаюсь разными вопросами морского дела, требующими приложения математики. За это время некоторые разделы математики приходилось прилагать чуть ли не ежедневно, другие ― раз в месяц, третьи ― раз в год, а были и такие, которые мне понадобились один раз в 45 лет.

Представьте себе, что я стал бы читать все эти разделы, и вот вам что-либо из этих разделов понадобилось через 37 лет; поверьте, что вы к тому времени так это забудете, что вам придется это как бы вновь выучить, прежде чем прилагать.

Хотя вы и готовитесь быть профессорами в нашей академии, но вы и теперь, и в будущем будете работать над практическим делом, которое всегда требует не столько общих рассуждений, а конкретного ответа; значит, прежде всего надо уметь производить численные вычисления быстро и верно. Численные вычисления вам понадобятся каждый день, поэтому методы их производства и должны быть усвоены в первую очередь.

В общем курсе вы изучали ряды и их общие свойства, но вы не имели практики в применении их к вычислениям с точки зрения быстрого и верного, с требуемой точностью, получения результата. Вы мне не поверите, что в точнейшей из наблюдательных наук ― астрономии ― нет ни одной точной формулы: всегда пользуются приближенными и получают результат с требуемой степенью точности не только быстрее, но, если можно так выразиться, "вернее", нежели по точной формуле. Вот этим и придется пополнить то, что вы знаете о рядах; в практике с этим вы будете встречаться раз в неделю.

Надо будет также показать вам, как интегрировать с требуемой степенью точности любое обыкновенное дифференциальное уравнение; это вам будет встречаться по крайней мере раз в месяц, а то и чаще. Раз в год будут вам встречаться обыкновенные дифференциальные уравнения, в которых требуется удовлетворить не только заданным начальным, но и заданным граничным условиям; мы постараемся пояснить и этот вопрос".

Конечно, перечень А. Н. Крылова отражает объем знаний по математике, требуемый прикладными задачами кораблестроения в современное А. Н. Крылову время. В другое время и для других специальностей перечень может быть и сокращен, и расширен.

Но неизменно плодотворной остается основная идея А. Н. Крылова — учить надо тому, что действительно потребуется в жизни; круг задач, с которыми будут повседневно сталкиваться выпускники учебного заведения, должен определять собой уровень и программу обучения.

Хотя замечания и пожелания А. Н. Крылова по преподаванию прикладной математики непосредственно адресованы высшим техническим учебным заведениям, они во многом относятся и к факультетам прикладной математики университетов. Действительно, положение этих факультетов двойственное: с одной стороны, они находятся в стенах университетов и испытывают давление традиций университетского преподавания математики; с другой стороны ― их выпускники будут сталкиваться со столь же конкретными прикладными задачами, как и выпускники технических вузов. В этих условиях учет исторического опыта поможет выработать правильный стиль преподавания.

С петербургской математической школы берет начало всемирная известность и авторитет российской математики (а не только отдельных гениальных ученых, как ранее). Несколько позже не меньшую известность получила московская математическая школа.