Задачи, приводящие к понятию тензора второго ранга

Валишин А.А., Ожерелкова Л. М.

«Ортогональные тензоры.
Теория и примеры»

Учебно-методическое пособие

Москва

УДК 51

ББК 22.1

Рецензент:

Д.ф.-м.н, профессор Ломовской В.А. (МИТХТ, каф. прикладной механики и основ конструирования).

Валишин А.А., Ожерелкова Л. М.

«Ортогональные тензоры. Теория и примеры».

Учебно-методическое пособие. М.: ИПЦ МИТХТ, 100 с.

Утверждено Библиотечно-издательской комиссией МИТХТ

им. М. В. Ломоносова в качестве учебно-методического пособия. Поз. 64 /2014.

В пособии излагаются основы теории ортогональных тензоров, т.е. тензорная алгебра и элементы тензорного анализа в прямоугольных системах координат. Именно теория ортогональных тензоров чаще всего используется в приложениях, в первую очередь, в механике сполошных сред и кристаллофизике. Изложение материала сопровождается многочисленными примерами и задачами с решениями. Пособие предназначено для студентов, обучающихся по направлению «Прикладная математика». Пособие может быть так же полезно студентам других специальностей, а также молодым преподавателям, аспирантам и научным сотрудникам.

© МИТХТ им. М.В. Ломоносова, 2014

Оглавление.

§1 Скаляры и векторы……………………………………………………. 4

§2. Задачи, приводящие к понятию тензора…………………………… 4

§3. Преобразование систем координат…………………………………. 11

§4. Правило суммирования Эйнштейна……………………………….. 15

§5. Преобразование координат точки и вектора………………………. 16

§6. Символ Кронекера…………………………………………………… 17

§7. Новое определние вектора…………………………………………… 19

§8. Задачи…………………………………………………………….……. 21

§9. Тензор второго ранга………………………………………….……… 24

§10. Транспонированный тензор………………………………………… 28

§11. Единичный тензор…………………………………………………… 28

§12. Симметричные и антисимметричные тензоры……………………. 28

§13. Задачи ……………………………………………………..…………. 30

§14. Геометрическая интерпретация тензоров первого и второго рангов 34

§15. Тензоры высших порядков………………………………………...… 36

§16. Операции с тензорами……………………………………………….. 38

§17. Теорема деления тензоров (критерий тензорности)………………. 41

§18. 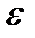-тензор леви-Чивиты (единичный тензор третьего ранга)…….. 42

§19. Бивектор………………………………………………………………. 46

§20. Двойственный вектор и двойственный тензор……………………. 49

§21. Векторное произведение как антисимметричный тензор………… 50

§22. Задачи ………………………………………………………………… 51

§23. Главные значения и главные направления симметричного

тензора второго ранга………………..………………………………. 59

§24. Степени тензоров второго ранга. Уравнение Гамильтона-Кэли… 67

§25. Круги Мора…………………………………………………………… 68

§26. Шаровой тензор и девиатор………………………………………… 73

§27. Нормальные и тангенциальные составляющие тензора

второго ранга……………………………………………………...…. 74

§28. Задачи ………………………………………………………………… 79

§29. Бескоординатная запись тензоров………………………………….. 92

§30. Тензорные поля. Дифференцирование и интегрирование тензоров 93

Список литературы……………………………………………….………… 99

Скаляры и векторы.

Из векторной алгебры известны понятия скаляра и вектора. Скалярами являются такие физические величины, как плотность, масса, объем, температура тела. Скаляры не связаны с понятием направления. При определении плотности или температуры бессмысленно говорить об изменении этих величин в каком-либо направлении. Такие ненаправленные физические величины называются скалярами. Значение скаляра полностью определяется заданием одного числа. Скаляры называются также тензорами нулевого ранга.

В отличие от скаляров, другой тип физических величин, называемых векторами, может быть определен только по отношению к направлению. Механическая сила, скорость, напряженность электрического или магнитного поля, плотность тока, температурный градиент и т.д. – хорошо известные примеры векторов. Чтобы полностью определить вектор, необходимо задать как его величину (модуль вектора), так и направление.

Можно определить вектор и по-другому. Рассмотрим прямоугольную декартову систему координат и зададим компоненты вектора вдоль каждой из осей координат. Компонента (или координата) вектора – это проекция вектора на данную ось. Если вектор 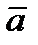имеет компоненты 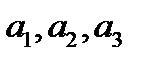, то это записывается в виде

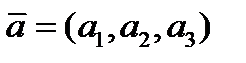(1)

Таким образом, когда оси координат выбраны, вектор полностью определяется заданием значений трех его компонент вдоль осей. Векторы называются также тензорами первого ранга.

Задачи, приводящие к понятию тензора второго ранга.

Рассмотрим два физических явления, для описания которых недостаточно знаний только о векторах.

Электропроводность кристаллов.

Рассмотрим проводник в электрическом поле. Электрическое поле – это векторное поле и характеризуется вектором напряженности поля 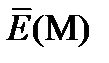, где 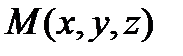– точка той области пространства, где задано поле. Электрическое поле – это потенциальное поле, т.е. существует такое скалярное поле 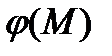, что его градиент пропорционален вектору 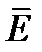, а именно

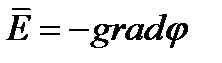(2)

Скалярное поле 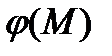называется потенциалом электрического поля. Можно провести аналогию между скалярным полем 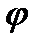и хорошо известным студентам МИТХТ скалярным полем температур 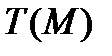. Скалярное температурное поле 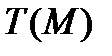порождает векторное поле своего градиента:

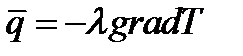(3)

Вектор 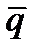, как известно, называется вектором плотности теплового потока и вполне аналогичен вектору напряженности .

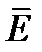Если в проводнике имеется электрическое поле, то в проводнике возникает электрический ток, характеризуемый вектором плотности тока 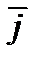. Вектор 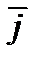определяет ток через единицу поверхности, перпендикулярную направлению тока. Если проводник изотропен и выполняется закон Ома, то вектор 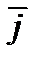параллелен вектору поля 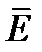и модуль 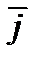пропорционален модулю 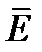. Поэтому можно записать:

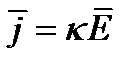(4)
где 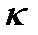– удельная электропроводность (рис 1а).

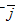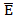Рис.1а)

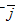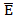Рис.1б)

Если в некоторой прямоугольной системе координат 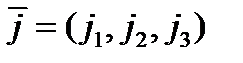и 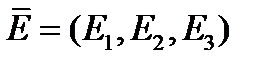, то формулу (4) можно переписать в виде:

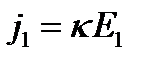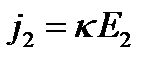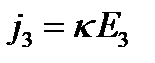, , (5)

т.е. компонента вектора 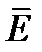порождает только одну компоненту вектора 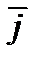вдоль той же оси.

Если же проводник представляет собой анизотропный кристалл, то соотношение между векторам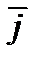и и 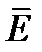не будет таким простым. Для кристаллов каждая компонента вектора 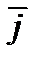линейно зависит от всех трех компонент поля 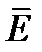, т.е.:

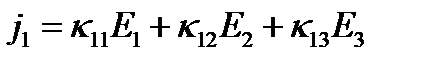
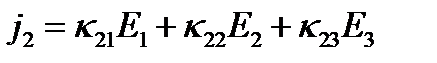(6)

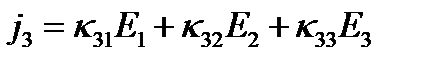
Отсюда следует, что вектор 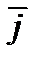не коллинеарен вектору 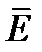(рис 1б). Каждый из коэффициентов 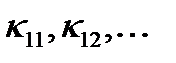имеет определенный физический смысл. Например, если поле приложено вдоль оси 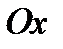(рис 2), то 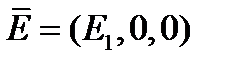и уравнения (6) принимают вид:

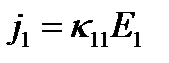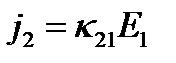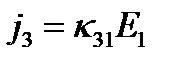, , (7)

Т.е. имеются компоненты тока 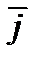не только вдоль оси 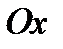, но и вдоль двух других осей.

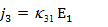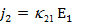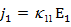Рис.2

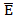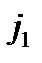Продольная компонента определяется коэффициентом 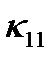, а две поперечные – коэффициентам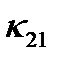и и 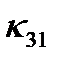. Аналогично, коэффициент 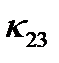определяет компоненту 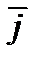, параллельную оси , когда поле приложено вдоль оси . Таким образом, для того чтобы определить электропроводность кристалла, нужно задать девять коэффициентов 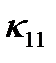, ,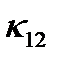… 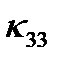. Для удобства их можно записать в виде матрицы:

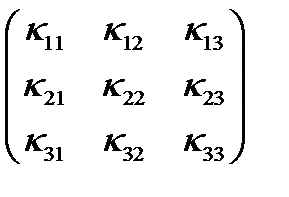(8)

Эта матрица обозначает тензор 2-го ранга, а элементы матрицы называются компонентами (или координатами) тензора. В данном случае он называется тензором электропроводности. Матрица тензора (8) записана для вполне определенной системы координат. Однако сам тензор электропроводности характеризует свойства кристалла независимо от системы координат. Не изменяется он и при изменении электрического поля в кристалле. Все это свидетельствует о том, что тензор электропроводности и другие, подобные ему тензоры, характеризующие свойства кристаллов, является инвариантным объектом, существующим независимо от системы координат и столь же реальным, как и сам кристалл. Но вот представление тензора (т.е. его компоненты) в разных системах координат различно. Это означает, что матрица (8) изменяется при изменении системы координат.

Нахождение правила, по которому преобразуются компоненты тензора при преобразовании системы координат, является одной из задач тензорного анализа.