Уровень значимости корреляции

Некоторые исследователи, вычислив значение коэффициента корреляции, на этом и останавливаются. Но с точки зрения грамотной методологии эксперимента следует определить и уровень значимости (то есть степень достоверности) данного коэффициента.

Уровень значимости коэффициента корреляции вычисляется при помощи таблицы критических значений. Ниже дан фрагмент указанной таблицы, позволяющий определить уровень значимости полученного нами коэффициента.

n	p = 0,1	p = 0,05	p = 0,01	p = 0,001
	0,582	0,666	0,798	0,898
	0,549	0,632	0,765	0,872
	0,521	0,602	0,735	0,847

Мы выбираем ту строку, которая соответствует объему выборки. В нашем случае
n = 10. Мы выбирает в данной строке то табличное значение, которое чуть меньше эмпирического (или точно равно ему, что бывает крайне редко). Это выделенное жирным шрифтом число 0,632. Оно относится к столбцу со значением уровня достоверности p = 0,05. То есть, фактически, эмпирическое значение занимает промежуточное положение между столбцами p = 0,05 и p = 0,01, следовательно, 0,05 ³ p ³ 0,01. Таким образом, мы отвергаем нулевую гипотезу и приходим к выводу, что полученный результат
(Rxy = 0,758) значим на уровне p < 0,05 (это уровень статистической значимости):
Rэмп > Rкр (p < 0,05) H0, Þ Н1! ст. зн.

На бытовом языке это можно проинтерпретировать следующим образом: можно ожидать, что эта сила связи будет иметь место в выборке реже, чем в пяти случаях из 100, если эта связь – следствие случайности.

Регрессионный анализ

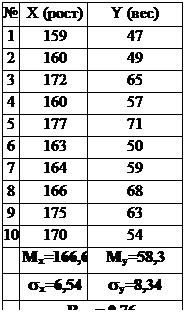Регрессионный анализ используется для изучения взаимосвязи между двумя величинами, измеренными в интервальной шкале. Этот вид анализа предусматривает построение регрессионного уравнения, позволяющего количественно описать зависимость одного признака от другого (коэффициент корреляции Пирсона указывает на наличие или отсутствие связи, но эту связь не описывает). Зная случайную величину одного из признаков и используя данное уравнение, исследователь может с определенной степенью вероятности предсказать соответствующее значение второго признака. Линейная зависимость признаков описывается уравнением следующего типа:

у = а + by * x ,

где а - свободный член уравнения, равный подъему графика в точкех=0 относительно оси абсцисс, b – угловой коэффициент наклона линии регрессии равный тангенсу угла наклона графика к оси абсцисс (при условии, что масштаб значений на обеих осях одинаков).

Зная значения исследуемых признаков, можно определить величину свободного члена и коэффициента регрессии по следующим формулам:

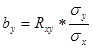
а = My – by * Mx

В нашем случае: ;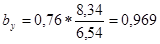

а = 58,3 – 0,97 * 166,6 = -103,3

Таким образом, формула зависимости веса от роста выглядит следующим образом:
у = 0,969 * х – 103,3

Соответствующий график приведен ниже.

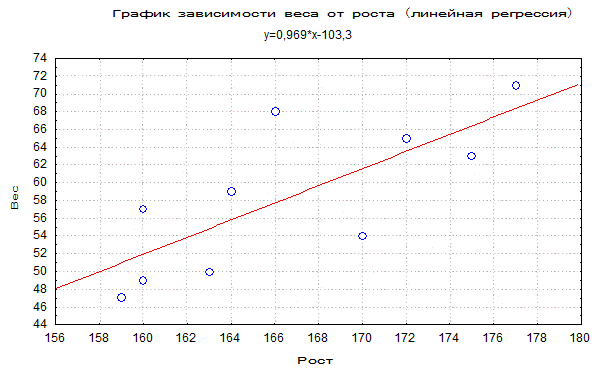
Если необходимо описать зависимость роста от веса (х от у), то значения а и b становятся другими и формулы необходимо соответствующим образом модифицировать:

x = а + bx * у

а = Mx – bx * My

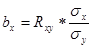
Изменяется в таком случае и вид графика. Это задание студентам будет предложено выполнить самостоятельно.

Коэффициент регрессии находится в тесной связи с коэффициентом корреляции. Последний представляет собой среднее геометрическое из коэффициентов регрессии признаков:

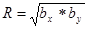
Квадрат коэффициента корреляции называется коэффициентом детерминации. Его величина определяет процентное взаимное влияние переменных. В нашем случае
R2 = 0,762 = 0,58. Это значит, что 58 % общей дисперсии Y объясняется влиянием переменной X, остальные 42 % обусловлены влиянием неучтенных в уравнении факторов.