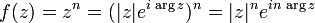Полиномиальные функции

I. Введение. 3

II. Элементарные функции. 4

Элементарные функции по Лиувиллю.. 4

Многочлен.. 5

Полиномиальные функции. 6

Рациональная функция. 7

Степенная функция. 7

Показательная функция. 8

Логарифм.. 10

Тригонометрические функции. 11

Обратные тригонометрические функции.. 14

III. Заключение. 21

IV. Список литературы. 21

I. Введение.

Термин «функция» появился в одной работе Лейбница в 1692г., а затем применялся братьями Якобом и Иоганном Бернулли для характеристики различных отрезков, так или иначе связанных с точками некоторой кривой. В 1718г. Иоганн Бернулли впервые даёт определение функции, свободное от геометрических представлений. Его ученик Эйлер в своём учебнике « Введение в анализ бесконечно малых» воспроизводит определение Бернулли, несколько его уточняя:

«Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и из чисел или постоянных количеств».

В течение ряда десятилетий существенного прогресса в определении понятия функции не было. Обычно приписывают Дирихле заслугу выдвижения на первый план идеи соответствия, которая лежит в основе этого понятия.

Задачи:

Ø Узнать, какие функции можно получить из основных элементарных функций;

Ø Узнать, какими свойствами обладают основные элементарные функции.

Цель:

ü Расширение кругозора своих знаний об основных элементарных функциях.

II. Элементарные функции.

Элементарные функции — функции, которые можно получить из основных элементарных функций:

• Полиномиальная функция,
• рациональная,
• степенная,
• показательная и логарифмическая,
• тригонометрические и обратные тригонометрические

с помощью конечного числа арифметических действий и композиций. Каждую элементарную функцию можно задать формулой, т.е. набором конечного числа символов, отвечающих перечисленным операциям.

Элементарные функции по Лиувиллю.

Рассматривая функции комплексного переменного, Лиувилль определил элементарные функции несколько шире. Элементарная функция y переменной x — аналитическая функция, которая может быть представлена как алгебраическая функция 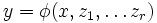от x и функций 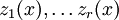, причем является логарифмом или экспонентой от некоторой алгебраической функции g₁ от x.

Например, sin(x) — алгебраическая функция от e^ix.

Не ограничивая общности рассмотрения, можно считать функции 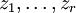алгебраически независимы, то есть если алгебраическое уравнение 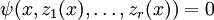выполняется для всех x, то все коэффициенты полинома 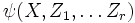равны нулю.

Многочлен.

В математике, многочлены или полиномы от одной переменной

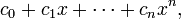
где c_i фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.

Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.

Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.

Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.

Полиномиальные функции.

Пусть A есть алгебра над кольцом R. Произвольный многочлен 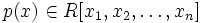определяет полиномиальную функцию

.

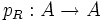Чаще всего рассматривают случай A = R.

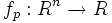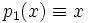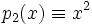В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены и из 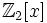определяют тождественно равные функции .

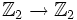Свойства:

• Кольцо многочленов над произвольной областью целостности само является областью целостности.
• Кольцо многочленов от любого конечного числа переменных над любым факториальным кольцом само является факториальным.
• Кольцо многочленов от одного переменного над полем является кольцом главных идеалов, т. е. любой его идеал может быть порожден одним элементом.
• Более того, кольцо многочленов от одного переменного над полем является евклидовым кольцом.

Рациональная функция.

Текущая версия (не проверялась)

Функция называется рациональной, если она может быть представлена в виде дроби:

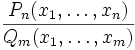
где 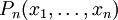, 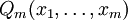— многочлены.

Такая функция определена во всех точках, кроме тех, в которых знаменатель 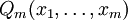обращается в ноль.

Свойства:

• Любое выражение, которое можно получить из переменных 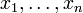с помощью четырёх арифметических действий, является рациональной функцией.
• Множество рациональных функций замкнуто относительно арифметических действий и операции композиции.
• Любая рациональная функция может быть представлена в виде суммы простейших дробей (см. Метод неопределённых коэффициентов), это применяется при аналитическом интегрировании.

Степенная функция.

Степенная функция комплексного переменного f(z) = zⁿ с целочисленным показателем определяется с помощью аналитического продолжения аналогичной функции вещественного аргумента. Для этого применяется показательная форма записи комплексных чисел.

А именно, известно, что любое комплексное число может быть представлено через его модуль и аргумент с помощью формулы Эйлера в виде z = | z | e^iargz. Пользуясь этим, запишем пока формальное выражение для степенной функции: