Метод, основанный на использовании теории массового обслуживания

Метод состоит в следующем:

- составляются уравнения массового обслуживания;

- выбираются начальные условия решения задачи;

- определяются вероятности застать изделие в исправном состоянии в любой момент времени и вероятно­сти безотказной работы;

- определяются в случае необходимости другие ко­личественные характеристики надежности.

Составление уравнений массового обслуживания

Перенумеруем возможные состояния изделия. В про­стейшем случае таких состояний будет два: изделие ис­правно («состояние «0») и изделие неисправно (состоя­ние «1»). При m-кратном общем резервировании изделия число возможных состояний равно m+2. Будем говорить, что имеет место i-е состояние, если неисправны i изделий (i=0, 1, 2,...,m+1).

Для составления искомых уравнений должны быть заданы:

- – интенсивность перехода из (i-1)-го со­стояния в i-е;

- – интенсивность обратного перехода из i-го состояния в (i-1)-е.

Для краткости будем в дальнейшем писать

,

Пусть 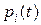– вероятность того, что в момент t имеет ме­сто i-е состояние. Сравнивая эти состояния в моменты t и t+Δt, по формуле полных вероятностей получаем

Здесь через обозначены величины второго по­рядка малости по сравнению с .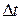

В пределе при приходим к системе дифферен­циальных уравнений:

(3.4.47)

Процесс изменения состояний рассматриваемой систе­мы изделий можно проиллюстрировать с помощью гра­фа, представленного на рис.31. Узлам графа соответст­вуют состояния системы (0,1,2,...,m+1), а ветвям – возможные переходы из одного состояния в другое.

Р и с. 31. Граф переходов системы при m-кратном общем резервировании

Искомая система дифференциальных уравнений мо­жет быть составлена с помощью графа совершенно меха­нически. Для этого необходимо при всех значениях i слева написать производную от вероятности 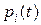, а справа просумми­ровать вероятности состояний, из кото­рых возможен переход в i-е состояние, предварительно умножив их соответствен­но на интенсивности этих переходов, и отнять вероятность 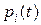, умноженную на сумму интенсивностей переходов из i-го состояния во все другие.

Приведенный на рис. 31 граф есть простой неветвящийся граф. Примером простого ветвящегося графа состояний системы массового обслуживания может служить граф, приведенный на рис. 32, где приняты обозначения:

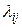- – интенсивность перехода из i-го состояния в состоя­ние j;

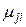- – интенсивность обратного перехода из j-го со­стояния в состояние i.

Рис. 32. Простой ветвящийся граф переходов системы

Тогда система дифференциальных уравнений массо­вого обслуживания будет иметь вид:

(3.4.48)

Так как при любом t сумма вероятностей всех воз­можных состояний системы равна единице, то сумма чле­нов правых частей систем (3.4.47) и (3.4.48) должна рав­няться нулю.

Система дифференциальных уравнений типа (3.4.47) и (3.4.48) может использовать­ся при определении следую­щих показателей:

- вероятности безотказ­ной работы резервирован­ных восстанавливаемых и невосстанавливаемых ремонти­руемых систем;

- функции и коэффици­ента готовности восстанав­ливаемых резервированных и нерезервированных систем при различных способах об­служивания;

- вероятности нахождения в данный момент времени на восстановлении к элементов;

- среднего времени пребывания системы в любом со­стоянии.

Выбор начальных условий решения задачи

Надежность восстанавливаемого изделия, как прави­ло, определяется при условии, что в момент включения все элементы исправны. Тогда

(3.4.49)

В общем случае в момент t = 0 изделие может нахо­диться в некотором состоянии j. Тогда

(3.4.50)

Определение вероятности застать изделие в исправном состоянии в любой момент времени

Вероятность застать изделие в исправном состоянии в любой момент времени находится путем решения урав­нений типа (3.4.47) и (3.4.48). Ограничимся рассмотрением системы типа (3.4.47).

При заданных начальных условиях эта система имеет единственное решение, причем для любого начального состояния существуют пределы

, (3.4.51)

где

(3.4.52)

Искомая вероятность 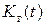находится из выражения

(3.4.53)

где n – последнее исправное состояние изделия (n≤m).

При m=0 (резервирование отсутствует) решение си­стемы (3.4.47) приводит к уже известному выражению (3.4.39), полученному ранее с помощью функции восста­новления.

Часто число состояний, в которых изделие неисправ­но, меньше, чем число состояний, в которых изделие ис­правно. В этом случае удобно вначале находить вероят­ность застать изделие в неисправном состоянии по формуле

, (3.4.54)

а затем – функцию готовности из выражения

(3.4.55)

Если изделие считается отказавшим только при нахождении его в состоянии m+1, то

(3.4.56)

Коэффициент готовности находится из (4.53) как установившееся значение 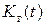, т.е

(3.4.57)

Определение вероятности безотказной работы и средней наработки до первого отказа

Вероятность безотказной работы находится путем ре­шения системы дифференциальных уравнений типа (3.4.47) и (3.4.48) при заданных начальных условиях. При этом в системах (3.4.47) и (3.4.48) исключаются в правой части те члены, которые содержат интенсивности переходов из отказовых состояний.

На практике иногда целесообразнее находить вероят­ность отказа изделия, так как отказовых состояний обыч­но меньше, чем исправных. Далее по известной вероятно­сти отказов находят вероятность безотказной работы.

Ограничимся рассмотрением системы (3.4.47) при усло­вии, что отказ наступает при выходе из строя всех m+1 устройств. В этом случае в системе (4.47) необходимо положить , а искомая вероятность безотказной работы есть вероятность того, что рассматриваемый слу­чайный процесс изменений состояний изделия за время t ни разу не окажется в поглощающем состоянии m+1. Обозначим решение этой новой системы уравнений через . Тогда

(3.4.58)

Если в начальный момент времени система находится в состоянии k=0, то средняя наработка до первого от­каза есть среднее время перехода из нулевого состояния в состояние m+1 и определяется выражением

(3.4.59)

В ряде прикладных задач теории надежности вероятность безотказной работы системы довольно точно определяется по приближенной формуле

(3.4.60)