Методы, основанные на использовании классической теории вероятностей
Если любые отказы непрерывно работающей системы устраняются мгновенно (все Yi=0), профилактика отсутствует, число восстановлений неограниченно, а все Xi являются независимыми одинаково распределенными случайными величинами с одной и той же плотностью распределения
 (3.4.1)
(3.4.1)
то моменты отказов образуют простой процесс восстановления.
Частным случаем простого процесса восстановления является пуассоновский процесс, для которого
 (3.4.2)
(3.4.2)
Если все условия для простого процесса восстановления выполнены за исключением того, что длительность от начала |работы до первого отказа имеет плотность распределения
 (3.4.3)
(3.4.3)
то такой процесс называется общим процессом восстановления. Общий процесс восстановления, для которого
 , (3.4.4)
, (3.4.4)
называется стационарным процессом восстановления.
Если в условиях простого процесса восстановления величины  и распределены одинаково с плотностью распределения
и распределены одинаково с плотностью распределения
 (3.4.5)
(3.4.5)
то такой процесс называется процессом восстановления с конечным временем восстановления.
В рассматриваемых случаях большую роль играет среднее число отказов за время t, называемое функцией восстановления, или среднее число замен H(t), причем для всех приведенных выше случаев имеем
 (3.4.6)
(3.4.6)
При n=1 получим:
- для простого процесса восстановления
 (3.4.7)
(3.4.7)
- для общего процесса восстановления
 (3.4.8)
(3.4.8)
При мгновенном восстановлении и n≥2
 (3.4.9)
(3.4.9)
В частном случае для стационарного процесса
 (3.4.10)
(3.4.10)
Из (4.6) следует, что при простом процессе восстановления H(t) удовлетворяет интегральному уравнению Вольтерра 2-го рода
 (3.4.11)
(3.4.11)
Переходя к преобразованию Лапласа, получаем
 , (3.4.12)
, (3.4.12)
где  ;
; 
Важную роль играет функция плотности восстановления, имеющая вид
 (3.4.13)
(3.4.13)
При простом процессе восстановления из (3.4.11) следует, что
 (3.4.14)
(3.4.14)
В теории надежности эта функция называется параметром потока отказов, т. е. 
Вероятность безотказной работы системы на участке  при
при  равна
равна
 (3.4.15)
(3.4.15)
Таким образом, h(t) приблизительно равна безусловной вероятности отказа за единицу времени, а интенсивность отказов
 (3.4.16)
(3.4.16)
равна условной вероятности отказа за единицу времени при условии, что до момента t отказов не было.
В частности, для стационарного процесса восстановления
 (3.4.17)
(3.4.17)
Известно, что если  при
при  , то
, то
 (3.4.18)
(3.4.18)
т. е. с течением времени процесс восстановления становится стационарным.
При нахождении h(t) через f(t) можно воспользоваться уравнением связи между преобразованием Лапласа для частоты отказов и средней частоты отказов, т. е.
 (3.4.19)
(3.4.19)
В случае конечного времени восстановления
 , (3.4.20)
, (3.4.20)
где
 (3.4.21)
(3.4.21)
Из 4.20 с учетом (4.9) и 4.21 следует, что
 , (3.4.22)
, (3.4.22)
где
 (3.4.23)
(3.4.23)
 (3.4.24)
(3.4.24)
Используя теорему нахождения преобразования Лапласа свёртки функций, получаем
 (3.4.25)
(3.4.25)
где
 (3.4.26)
(3.4.26)
 (3.4.27)
(3.4.27)
Различные предельные выражения для процесса восстановления можно найти, используя теорему Смита, согласно которой
 , (3.4.28)
, (3.4.28)
где  - любая невозрастающая, интегрируемая функция на участке (0,∞).
- любая невозрастающая, интегрируемая функция на участке (0,∞).
Изложенные элементы теории позволяют найти функцию готовности 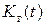 , равная, по определению, вероятности того, что в момент t система исправна.
, равная, по определению, вероятности того, что в момент t система исправна.
Система будет исправна в момент t при осуществлении одного из следующих несовместимых событий:
- за время t система не отказала;
- за время t система отказывала и восстанавливалась ровно n раз (n=1,2,…), причём последний ремонт произошёл на участке  и за оставшееся время
и за оставшееся время  система больше не отказывала.
система больше не отказывала.
Вероятность первого события равна
 ,
,
а второго—порядка
 .
.
Устремим  к нулю и просуммируем по всем x от 0 до t и по всем n от 1 до ∞. В итоге получаем, что вероятность безотказной работы системы в момент t при наличии отказов и ремонтов равна
к нулю и просуммируем по всем x от 0 до t и по всем n от 1 до ∞. В итоге получаем, что вероятность безотказной работы системы в момент t при наличии отказов и ремонтов равна
 , (3.4.29)
, (3.4.29)
где  есть плотность процесса, образованного моментами
есть плотность процесса, образованного моментами

Следовательно,
 (3.4.30)
(3.4.30)
Стационарное значение функции готовности (коэффициент готовности) можно найти с помощью теоремы Смита.
Так как  , а математическое ожидание Т случайной величины Xn+Yn (расстояние между соседними точками рассматриваемого случайного процесса) при любых n равно
, а математическое ожидание Т случайной величины Xn+Yn (расстояние между соседними точками рассматриваемого случайного процесса) при любых n равно

то по теореме Смита имеем
 (3.4.31)
(3.4.31)
Аналогично определяется вероятность  того, что система проработает безотказно на заданном участке
того, что система проработает безотказно на заданном участке  . Имеем
. Имеем
 (3.4.32)
(3.4.32)
В стационарном случае
 (3.4.33)
(3.4.33)
Рассмотрим очень важный для теории надежности случай, когда
 , (3.4.34)
, (3.4.34)
где μ – интенсивность восстановления.
В данном случае
 ,
,  (3.4.35)
(3.4.35)
Тогда, используя (4.13), (4.25)-(4.27), получаем
 (3.4.36)
(3.4.36)
Аналогично, из уравнения (4.30) следует:
 (3.4.37)
(3.4.37)
Так как  , то
, то

 (3.4.38)
(3.4.38)
Отсюда
 (3.4.39)
(3.4.39)
Положив в (3.4.33)
 ,
,
получаем, что вероятность безотказной работы на заданном участке  равна
равна
 (3.4.40)
(3.4.40)
При  получаем стационарное значение этой вероятности:
получаем стационарное значение этой вероятности:
 (3.4.41)
(3.4.41)
При решении большого класса задач удобно исходить из вероятностей нахождения системы в том или ином состоянии. В общем случае число таких состояний будет больше двух, но при решении задач теории надежности обычно приходится иметь дело с конечным или по меньшей мере со счетным числом состояний.
Пусть в момент t система находится в состоянии i. Если вероятность  перехода системы за время τ из состояния i в состояние j не зависит от поведения системы до момента t, то такой случайный процесс называется марковским процессом. Если эта вероятность не зависит также от момента t, то имеет место однородный марковский процесс.
перехода системы за время τ из состояния i в состояние j не зависит от поведения системы до момента t, то такой случайный процесс называется марковским процессом. Если эта вероятность не зависит также от момента t, то имеет место однородный марковский процесс.
Для этого случая можно найти характеристики надежности путем решения различных интегральных, дифференциальных и интегро-дифференциальных уравнений.
Например, пусть по-прежнему требуется найти коэффициент готовности 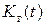 . Если система исправна, будем говорить, что она находится в состоянии «0», если неисправна и восстанавливается – в состоянии «1». Обозначим вероятности нахождения системы в момент t в этих состояниях через
. Если система исправна, будем говорить, что она находится в состоянии «0», если неисправна и восстанавливается – в состоянии «1». Обозначим вероятности нахождения системы в момент t в этих состояниях через  и
и  соответственно. Естественно, что
соответственно. Естественно, что
 (3.4.42)
(3.4.42)
При экспоненциальном законе распределения времени безотказной работы  и произвольном законе распределения времени восстановления
и произвольном законе распределения времени восстановления  вероятность
вероятность  можно представить в виде
можно представить в виде
 (3.4.43)
(3.4.43)
Подставляя (4.43) в (4.42), получаем

или
 (3.4.44)
(3.4.44)
Так как  , то выражение (3.4.44) принципиально позволяет вычислить
, то выражение (3.4.44) принципиально позволяет вычислить 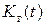 при любом законе распределения времени восстановления.
при любом законе распределения времени восстановления.
При произвольном законе распределения времени безотказной работы F(t) и экспоненциальном законе распределения времени восстановления  вероятность
вероятность  можно представить в виде
можно представить в виде
 (3.4.45)
(3.4.45)
Заменяя в (4.45)  на
на  и переходя к преобразованию Лапласа, получаем
и переходя к преобразованию Лапласа, получаем
 (3.4.46)
(3.4.46)
Если в (4.44) и (4.46) подставить  и
и  соответственно, получим уже известное выражение (4.38).
соответственно, получим уже известное выражение (4.38).
При экспоненциальном законе распределения и наличии ряда исправных состояний наиболее распространенный метод нахождения 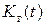 состоит в составлении и решении дифференциальных уравнений. Методика их составления описана в следующем пункте. Однако при неэкспоненциальном законе распределения сложность решения задач резко возрастает. В этих случаях на практике в основном нашли применение методы, связанные с решением интегральных и интегро-дифференциальных уравнений.
состоит в составлении и решении дифференциальных уравнений. Методика их составления описана в следующем пункте. Однако при неэкспоненциальном законе распределения сложность решения задач резко возрастает. В этих случаях на практике в основном нашли применение методы, связанные с решением интегральных и интегро-дифференциальных уравнений.
