Тема 3. Формула полной вероятности и формула Байеса

Иногда о ситуации, в которой проводится опыт можно высказать некоторые предположения, при которых опыт протекает уже более просто. Такого рода предположения называются гипотезами.

Следствием двух основных теорем теории вероятностей – теоремы сложения и теоремы умножения – являются формула полной вероятности и формула Байеса.

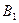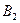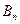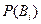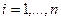Теорема. Пусть на заданном вероятностном пространстве определена полная группа несовместных событий , ,…, и событие может появиться с одним из данных событий. Вероятности , , заданы, условные вероятности 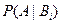также заданы для всех 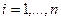. Тогда справедлива формула полной вероятности

.

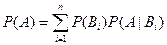События 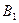, ,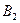…, 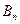называются гипотезами.

Пример 1. В цехе три группы станков производят одни и те же детали. Производительность их одинакова, но качество работы различно. Известно, что станки первой группы дают 3% брака, второй группы – 5 %, третьей – 4%. Все произведенные в цехе детали сложены на складе. Найти вероятность того, что наугад взятая деталь окажется бракованной, если станков первой группы 5 штук, второй – четыре, третьей – три.

Решение. Обозначим событие

– деталь бракованная.

Рассмотрим три гипотезы:

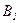– деталь первой группы,

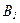- деталь второй группы,

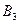– деталь третьей группы.

Тогда искомая вероятность вычисляется по формуле

.

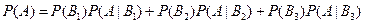Что означает каждая вероятность?

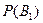– вероятность того, что взятая деталь оказалась сделанной станками 1 группы,

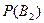– вероятность того, что взятая деталь оказалась сделанной станками 2 группы,

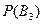– вероятность того, что взятая деталь оказалась сделанной станками 3 группы.

Всего станков 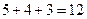. Тогда

, , .

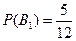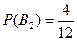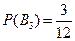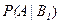– вероятность того, что взятая деталь оказалась бракованной, при условии, что она сделана станками 1-ой группы; .

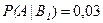Аналогично , .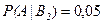

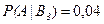Имеем

.

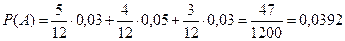Пример 2. Имеется две урны. В первой лежат 3 белых и 4 черных шара, во второй – 5 белых и 2 черных. Наудачу выбирается урна и из нее вынимается шар. Какова вероятность того, что этот шар белый?

Решение. Обозначим через событие «вынут белый шар».

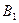- выбрана первая урна,

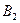- выбрана вторая урна.

Тогда 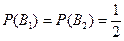поскольку эти события равновозможны.

Найдем условные вероятности.

Вероятность того, что вынут белый шар при условии, что выбрана первая урна, равна

.

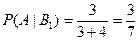Вероятность того, что вынут белый шар при условии, что выбрана вторая урна, равна

.

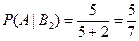Тогда по формуле полной вероятности получаем вероятность события

.

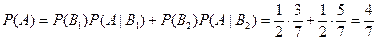Следствием формулы полной вероятности является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез 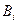, принятых до опыта и называемых априорными («a priori» - доопытные) по результатам уже проведенного опыта, т.е. найти условные вероятности 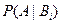, которые называются апостериорными («a posteriori» - послеопытные).

Формула Байеса позволяет находить вероятности гипотез при условии, что произошло событие .

Теорема. Пусть на заданном вероятностном пространстве определена полная группа несовместных событий 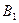, ,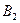…, 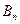и событие может появиться с одним из данных событий. Вероятности 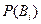, , 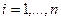заданы, условные вероятности 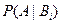также заданы для всех 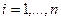. Тогда справедлива формула

.

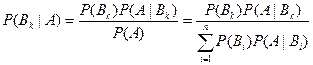Пример 3. В урне лежит шар: либо белый, либо черный. В урну кладут белый шар. Затем вынимают из урны шар. Этот шар оказался белым. Какова вероятность того, что в урне остался белый шар.

Решение. Введем обозначения 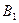- в урне лежал белый шар,

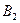- в урне лежал черный шар,

- из урны достали белый шар.

Белый шар в урне после того, как из нее вынули белый шар, может остаться только в том случае, когда там изначально лежал белый шар. Т.е. необходимо найти вероятность .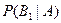

Вероятности событи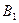й и 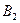равны

.

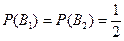Условные вероятности

, .

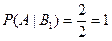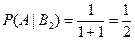Тогда .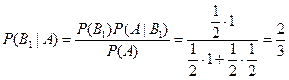

Пример 4. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.

Решение. Введем обозначения

– деталь отличного качества,

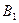– деталь произведена первым автоматом,

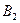– деталь произведена вторым автоматом.

Вопрос задачи сводится к нахождению вероятности .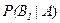

Используем формулу Байеса

.

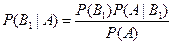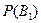– вероятность того, что деталь произведена первым автоматом.

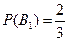, так как производительность 1-го автомата в 2 раза больше производительности второго;

.

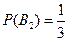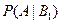– вероятность того, что деталь хорошего качества, при условии, что ее сделал первый автомат

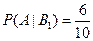
Аналогично .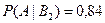

По формуле Байеса

.
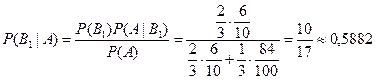