Классификация случайных событий

1. Событие называется невозможным, если оно не может произойти в результате данного опыта. Невозможное событие обозначается Ø.

2. Достоверное событие – это событие, которое в данном опыте всегда происходит. Обозначается .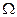

3. Событие 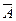называется противоположным событию , если оно заключается в ненаступлении события .

4. Событие 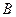называется подсобытием события , если при наступлении события 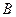всегда наступает событие .

5. Если событие 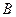является подсобытием и событие является подсобытием 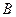, то события и 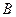называются эквивалентными.

6. События 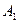, ,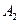…, 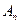называются несовместными, если ни одно из них не может появиться вместе с другим.

7. Говорят, что события 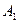, ,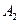…, 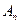образуют полную группу событий, если в результате опыта происходит хотя бы одно из этих событий.

Замечание: Элементарные события образуют полную группу несовместных событий.

Действия над событиями.

1. Объединением (суммой) двух событий и 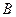называется событие 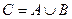, которое заключается в появлении хотя бы одного из этих событий (т.е. либо 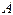, либо 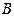, либо 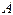и 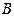вместе). Если события несовместны, то пишут .

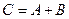2. Пересечением (произведением) двух событий и 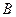называется событие 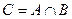, которое заключается в одновременном появлении этих событий (т.е А и В одновременно).

3. Разностью двух событий и 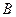называется событие 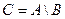, которое заключается в появлении события и не появлении .

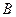Вероятность и ее свойства.

Любому событию можно поставить в соответствие некоторую числовую характеристику, которая определяет степень возможности появления данного события в конкретных условиях и называется вероятностью.

Вероятность события обозначается .

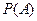Вероятность удовлетворяет трем аксиомам Колмогорова:

1. Аксиома неотрицательности: .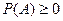

2. Аксиома нормировки: .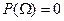

3. Аксиома аддитивности: если события 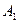, ,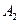…, 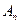несовместны, то .

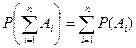Свойства вероятности

1. Вероятность невозможного события равна 0.

2. Вероятность противоположного события равна

.

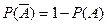3. Если событие 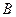является подсобытием , то

.

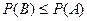4. Вероятность любого события не превосходит 1:

.

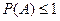5. Для любых событий и 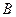справедливо равенство .

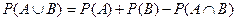Классическое определение вероятности

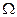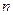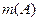Пусть пространство элементарных событий содержит элементарных событий, вероятности которых одинаковы. Пусть наступлению события благоприятствует элементарных событий. Тогда вероятность события определяется по формуле

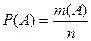
Классическое определение вероятности применимо, когда пространство элементарных событий конечно и элементарные события равновозможны.