Расчет и анализ систем подчиненного регулирования

Цель работы–освоение методики расчета и изучение свойств систем подчиненного регулирования.

Основные сведения

Системы подчиненного регулирования (СПР) построены по каскадному принципу, т. е. с вложенными друг в друга (подчиненными) контурами. Выходная величина регулятора i-го контура служит задающим воздействием для (i –1)-го контура. Каждый контур содержит регулятор с ПФ 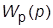, звенья с малыми постоянными времени 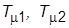и т. д. 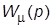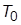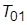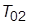(часто одним из таких звеньев является подчиненный по отношению к данному контур) с общей ПФ и звено с одной ( ) или двумя ( и ) большими постоянными времени, имеющее ПФ 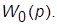Внутри каждого контура регулятор осуществляет последовательную коррекцию, компенсируя большую постоянную времени, являющуюся причиной нежелательной инерционности объекта управления.

Параметры регуляторов рассчитываются по формулам, определяющим тип стандартной настройки контура. Наиболее широко применяются настройки на оптимум по модулю (ОМ) и на симметричный оптимум (СО).

Пусть 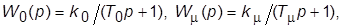обратную связь полагаем единичной. Чтобы обеспечить настройку на ОМ, необходимо применить ПИ-регулятор с ПФ 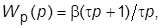параметры которого следует рассчитать по формулам 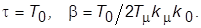Переходная характеристика контура по задающему воздействию имеет следующие показатели качества: 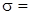4.3%, 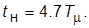Быстродействие контура, таким образом, определяется только значением малой постоянной времени. Недостаток этой настройки состоит в том, что время реакции на возмущающее воздействие зависит не только от 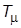, но и от .

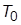Если 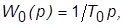то настройка на ОМ обеспечивается применением П-регулятора с ПФ 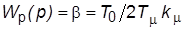. Для того же, чтобы настроить контур на СО, следует применить ПИ-регулятор, выбрав его параметры

следующим образом: 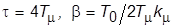. Показатели качества ПХ контура по задающему воздействию таковы: 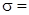43%, 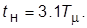Длительность переходного процесса по возмущению зависит только от .

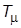В многоконтурной системе при расчете регулятора вышестоящего контура подчиненный ему контур, настроенный на ОМ, рассматривается приближенно как апериодическое звено с эквивалентной малой постоянной времени 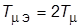. Если в контуре есть несколько звеньев с малыми постоянными времени, то их допустимо рассматривать как одно апериодическое звено с постоянной времени, равной сумме указанных малых постоянных времени.

Программа работы

Объектом исследования является система регулирования скорости двигателя постоянного тока, схема которой (в относительных единицах) приведена на рисунке. Питание двигателя осуществляется от тиристорного преобразователя. Система содержит подчиненный контур регулирования тока.

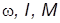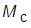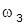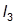
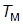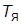Ввиду его высокого быстродействия обратная связь по противоЭДС двигателя не учтена. На схеме и – угловая скорость, ток, электромагнитный момент и момент сопротивления двигателя; и – задающие воздействия для скорости и тока; и – электромеханическая и электромагнитная постоянные времени двигателя; 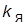– коэффициент передачи якорной цеп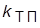и; и 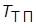– коэффициент передачи и постоянная времени тиристорного преобразователя; 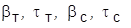– параметры ПИ‑регулято­ров тока и скорости.

Значения параметров объекта управления приведены в таблице.

Параметр	Вариант
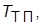с	0.004	0.004	0.005	0.004	0.004	0.005	0.004	0.004	0.005	0.005
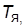с	0.01	0.02	0.04	0.01	0.02	0.04	0.01	0.02	0.04	0.05
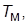с	0.1	0.2	0.4	0.1	0.2	0.4	0.1	0.2	0.4	0.5

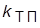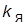Для выполнения работы необходимо сделать следующее:

1. Рассчитать параметры регулятора тока и далее ­– регулятора скорости по формулам, приведенным в 4.1, исходя из того, что контуры тока и скорости должны быть настроены, соответственно, на ОМ и СО. При расчете регулятора скорости рассматривать контур тока как апериодическое звено.

2. Исследовать динамические свойства контура тока. С этой целью получить его ПХ, подавая на вход контура единичное ступенчатое воздействие 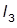. Сделать эскиз ПХ или копию экрана, определить 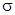и 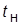, сравнить их с теоретическими значениями. Далее, разомкнув обратную связь, получить ЛЧХ контура тока. Определить запас устойчивости по фазе.

3. Исследовать динамические свойства контура скорости с идеализированным контуром тока, для чего получить ПХ системы (см. рисунок) по задающему воздействию, заменив контур тока апериодическим звеном с эквивалентной малой постоянной времени.

4. Исследовать динамические свойства системы (рисунок) по задающему воздействию: получить ПХ 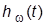, определить 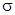и 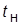, сравнить со значениями, полученными в п. 3. Прокомментировать результат.

5. Определить порядок астатизма 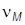системы по возмущению 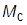. Получить ПХ 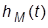по возмущению, определить ее установившееся значение 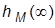и время регулирования 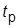(задавать допуск для отклонения 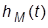от 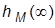как 0.05 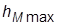). Повторить анализ, увеличив значение 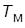вдвое и пересчитав значение 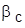. Прокомментировать результаты.

Содержание отчета

1. Структурная схема, значения параметров объекта управления, расчет параметров регуляторов.

2. Передаточные функции и построенные по ним асимптотические ЛАХ разомкнутых контуров тока и скорости (в последнем случае контур тока рассматривается как апериодическое звено).

3. Переходные характеристики контуров тока и скорости по задающим воздействиям, значения 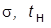и 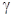. Выводы на основании сравнения с теоретическими значениями.

4. Анализ порядка астатизма по возмущению. ПФ по возмущению. Значения 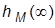и 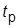для двух значений 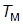. Комментарии результатов.

Контрольные вопросы

1. Как в зависимости от ПФ объекта следует выбирать тип регулятора и по каким формулам определяют его параметры при настройке на ОМ и СО?

2. Получить формулы для расчета параметров ПИД-регулятора при настройке контура на ОМ, если ПФ 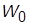описывает апериодическое звено второго порядка с постоянными времен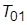и и .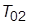

3. Пояснить, каковы принципы настройки контуров на ОМ и СО (с помощью асимптотических ЛАХ).

4. Какими значениями показателей качества ПХ и частотных показателей качества характеризуются ОМ и СО?

5. Почему несколько звеньев с малыми постоянными времени при расчете СПР можно заменять одним звеном с суммарной постоянной времени?

Лабораторная работа № 5