Основной закон теплопроводности – закон Фурье

Методические указания

к практическим занятиям

по дисциплине «Тепломассообмен»

для студентов специальности 290700 (270109)

«Теплогазоснабжение и вентиляция»

Ставрополь, 2012

В методических указаниях для студентов специальности 290700 (270109) к практическим занятиям приводится методика расчетов в реальных элементах конструкции теплотехнических устройств (стенка топочной камеры, парогенерирующая труба, трубопровод горячей воды и др.).

Для выполнения расчетов приводятся данные по определению теплофизических параметров теплоносителей и конструкционных материалов.

Составители: доцент - Гейвандов И.А.

доцент – Богачев В.В.

Рецензент: доцент Стоянов Н.И.

1. Введение

Базовыми дисциплинами для дисциплины «Тепломассообмен» являются такие дисциплины, как: «Высшая математика», «Физика». Дисциплина «Тепломассообмен» является основополагающие для студентов специальности 270901 «Теплогазоснабжение и вентиляция». В ней заложены основы понимание студентами таких профессиональных дисциплин, как «Отопление», «Вентиляция», «Теплоснабжение», «Теплогенерирующие установки» и т.д.

2. Цели и задачи

Целью практических занятий является систематизация, закрепление и углубление теоретических и практических знаний, полученных в лекционном курсе, а так же при проведении лабораторных работ.

Задачей практических занятий является усвоение студентами методики применения знаний и умений при решении конкретных задач по избранной специальности.

ПЗ №1. Теплопроводность

Теоретическая часть

ТЕПЛОПРОВОДНОСТЬ

Основной закон теплопроводности – закон Фурье

Закон Фурье устанавливает связь между характеристиками температурного поля в любой его точке и формулируется следующим образом.

Удельный тепловой поток при теплопроводности пропорционален градиенту температуры и направлен в обратную сторону по отношению к градиенту температуры. Математическое выражение закона Фурье имеет вид:

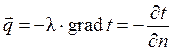. (1.1)

Знак (–) учитывает, что вектор теплового потока направлен противоположно вектору градиента температуры.

Коэффициент пропорциональности ( 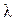) называется коэффициентом теплопроводности, имеет размерность Вт/(м×К) и является важной характеристикой способности тел передавать или задерживать тепло при теплопроводности.

Количественно коэффициент теплопроводности ( 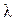) условно выражает удельный тепловой поток (q, Вт/м²), проходящий через слой вещества толщиной 1 м при разности температур 1 К (grad t = 1).

Наименьшее значение коэффициент теплопроводности имеет для газов и меняется в диапазоне от 0,01 до 0,1 Вт/(м×К). С ростом температуры коэффициент теплопроводности растет и для большинства газов в среднем равен 0,02 – 0,03 Вт/(м×К).

В газах процесс теплопроводности в чистом виде существует только в очень тонких слоях газа, примыкающих к твердой поверхности, т. к. с увеличением толщины слоя возникает конвекция.

Для жидкостей величина коэффициента теплопроводности занимает промежуточное значение между газами и твердыми телами. Среднее значение коэффициента теплопроводности жидкостей лежит в диапазоне от 0,1 до 0,7 Вт/(м×К) и уменьшается с увеличением температуры (за исключением воды и глицерина).

Для воды коэффициент теплопроводности растет от 0,55 до 0,685 Вт/(м×К) с увеличением температуры от 0 до 127 ⁰С, а затем незначительно уменьшается.

Для твердых тел коэффициент теплопроводности имеет максимальное значение и в среднем меняется от 1,0 до 400 Вт/(м×К).

По величине коэффициента теплопроводности все твердые тела делятся на две группы: проводники тепла и теплоизоляционные материалы.

Проводниками тепла обычно являются металлы, среди которых наибольший коэффициент теплопроводности имеют чистые металлы за счет движения свободных электронов, что обеспечивает так же высокую электропроводность.

Наивысший коэффициент теплопроводности у серебра – 430 Вт/(м×К), следом идут медь (350 – 400 Вт/(м×К)), алюминий (200 – 230 Вт/(м×К)), железо (75 Вт/(м×К)), свинец (40 Вт/(м×К)) и т. д. Теплопроводность металлических сплавов всегда меньше теплопроводности чистых металлов, например: латунь – 110 Вт/(м×К), бронза – 60 Вт/(м×К), углеродистая сталь – 45 – 50 Вт/(м×К), легированная сталь – 15 – 20 Вт/(м×К) и т. д.

Теплоизоляционные свойства твердых тел обусловлены наличием в их объеме мелких газовых включений, конвективный перенос тепла в которых очень мал.

В зависимости от характера газовых включений различают вспененные и волокнистые изоляционные материалы.

Наилучшими теплоизоляционными свойствами обладают материалы из вспененных пластмасс или неорганических материалов, например: пенополиуретан – 0,04 Вт/(м×К), пенополистирол (пенопласт) – 0,05 Вт/(м×К), пеностекло – 0,12 Вт/(м×К), газо– и пенобетон – 0,15 – 0,2 Вт/(м×К) и т. д.

Волокнистые изоляционные материалы, состоящие из объема, заполненного волокнами из органических или неорганических материалов, имеют более высокую теплопроводность, например: плиты стекловатные – 0,05 – 0,06 Вт/(м×К), плиты минераловатные – 0,06 – 0,08 Вт/(м×К), войлок строительный 0 0,07 – 0,09 Вт/(м×К) и т. д.

С ростом температуры коэффициент теплопроводности изоляционных материалов увеличивается, что связано с наличием газовых включений в их объеме. Обычно эту зависимость представляют в следующем виде:

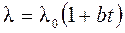, (1.2)

где 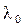– начальное значение коэффициента теплопроводности при t = 0 ⁰С, Вт/(м×К);

b – эмпирический коэффициент, Вт/м.

Уравнение Фурье дает математическое описание произвольного температурного поля в дифференциальной форме.

Для получения расчетных зависимостей процесса теплопроводности в конкретных условиях необходимо дифференциальное уравнение Фурье дополнить математическим описанием всех частных особенностей конкретного процесса.

Таковыми особенностями являются условия однозначности (размеры, форма, физические характеристики тела, температурные условия и т. д.) и краевые условия (начальные и граничные условия).

В качестве примера рассматривается решение задачи теплопроводности для наиболее простых, но практически важных случаев – теплопроводность плоской и цилиндрической стенки в стационарных условиях.