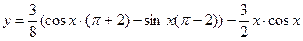Линейные неоднородные уравнения
Структура общего решения линейного неоднородного уравнения, т. е. уравнения с правой частью: 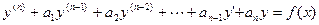
определяется следующей теоремой.
Если и = и(х) — частное решение неоднородного уравнения, а 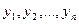 — фундаментальная система решений соответствующего однородного уравнения, то общее решение линейного неоднородного уравнения имеет вид
— фундаментальная система решений соответствующего однородного уравнения, то общее решение линейного неоднородного уравнения имеет вид
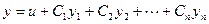
Иными словами, общее решение неоднородного уравнения равно сумме любого его частного решения и общего решения соответствующего однородного уравнения.
Следовательно, для построения общего решения неоднородного уравнения надо найти одно его частное решение (предполагая уже известным общее решение соответствующего однородного уравнения).
Рассмотрим два метода отыскания частного решения линейного неоднородного уравнения.
Метод подбора частного решения (метод неопределенных коэффициентов). Этот метод применим только к линейным уравнениям с постоянными коэффициентами и только в том случае, когда его правая часть имеет следующий вид:
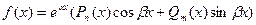
(или является суммой функций такого вида).Уравнение в таком случае называют дифференциальным линейным неоднородным уравнением 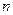 -го порядка со специальной правой частью. Здесь
-го порядка со специальной правой частью. Здесь 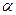 и
и 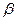 — постоянные, Рп (х) и Qm(x) — многочлены от х соответственно n-й и m-й степени.
— постоянные, Рп (х) и Qm(x) — многочлены от х соответственно n-й и m-й степени.
Частное решение уравнения 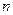 -го порядка
-го порядка 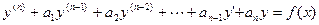 ,
,
где f (х) имеет указанный вид, а 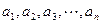 - действительные постоянные коэффициенты, следует искать в виде
- действительные постоянные коэффициенты, следует искать в виде 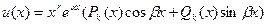 , где
, где 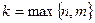 ,
,
а 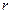 равно показателю кратности корня
равно показателю кратности корня 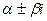 в характеристическом уравнении
в характеристическом уравнении 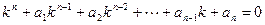 . Если характеристическое уравнение такого корня не имеет, то следует положить
. Если характеристическое уравнение такого корня не имеет, то следует положить 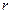 = 0;
= 0;
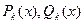 — полные многочлены от х степени k с неопределенными коэффициентами.
— полные многочлены от х степени k с неопределенными коэффициентами.
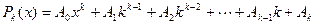
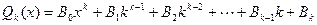
Подчеркнем, что многочлены Pk (x) и Qk (x) должны быть полными:то есть содержать все степени х от нуля до k с различными неопределенными коэффициентами при одних и тех же степенях х в обоих многочленах, и что при этом, если в выражение функции 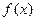 входит хотя бы одна из функций
входит хотя бы одна из функций 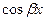 или
или 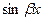 , то в и (х), надо всегда вводить обе функции.
, то в и (х), надо всегда вводить обе функции.
Неопределенные коэффициенты можно найти из системы линейных алгебраических уравнений, получаемых отождествлением коэффициентов подобных членов в правой и левой частях исходного уравнения, после подстановки в него 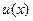 вместо у.
вместо у.
.
Проверку правильности выбранной формы частного решения дает сопоставление всех членов правой части уравнения с подобными им членами левой части, появившимися в ней после подстановки 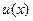 .
.
Если правая часть исходного уравнения равна сумме нескольких различных функций рассматриваемой структуры, то для отыскания частного решения такого уравнения нужно использовать теорему наложения решений: надо найти частные решения, соответствующие отдельным слагаемым правой части, и взять их сумму, которая и является частным решением исходного уравнения.
Примечание. Частными случаями функции f (х) рассматриваемой структуры (при наличии которых в правой части уравнения применим метод подбора частного решения) являются следующие функции:
1) 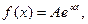 где А-постоянная.
где А-постоянная. 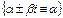
2) 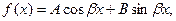 где А и В-постоянные.
где А и В-постоянные. 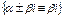
3) 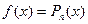 ,(многочлен степени
,(многочлен степени 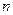 ),
), 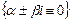 .
.
4) 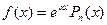 ,
, 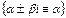
5) 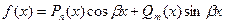 ,
, 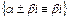
6) 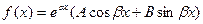 , где А и В-постоянные
, где А и В-постоянные
Пример 12.1. Найти частное решение уравнения 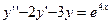 , удовлетворяющее краевым условиям (т.е. условиям , заданным в двух различных точках множества решений, через которые « провешивается » интегральная кривая)
, удовлетворяющее краевым условиям (т.е. условиям , заданным в двух различных точках множества решений, через которые « провешивается » интегральная кривая) 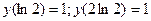 .
.
Характеристическое уравнение 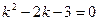 имеет корни
имеет корни 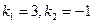 . Общее решение соответствующего однородного уравнения
. Общее решение соответствующего однородного уравнения 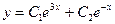 .Частное решение исходного уравнения следует искать в виде
.Частное решение исходного уравнения следует искать в виде 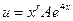 ,где
,где 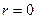 ,так как общие корни однородного уравнения и правой части отсутствуют.
,так как общие корни однородного уравнения и правой части отсутствуют.
Пусть 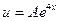 ,
,
Тогда 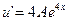 , а
, а
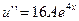 .
.
Подставим в исходное уравнение 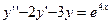 найденное частное решение и получим
найденное частное решение и получим 
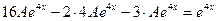 .
.
Сокращая на 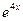 , и приводя подобные члены - получим
, и приводя подобные члены - получим 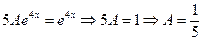
Следовательно, общее решение данного уравнения 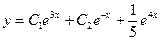
Для нахождения 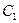 и
и 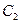 воспользуемся краевыми условиями:
воспользуемся краевыми условиями:
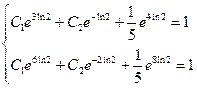 или
или 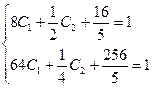
Отсюда 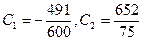 .Общее решение данного уравнения имеет вид
.Общее решение данного уравнения имеет вид 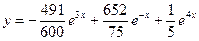 .
.
Пример 12.2. Найти решение уравнения 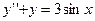 , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям 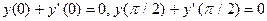 .
.
Характеристическое уравнение 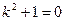 имеет корни
имеет корни 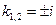 а потому общее решение однородного уравнения
а потому общее решение однородного уравнения 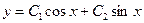 . Частное решение следует искать в виде
. Частное решение следует искать в виде 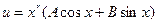 ,где
,где 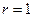 ,так как
,так как 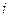 -общий простойкорень характеристического уравнения. Пусть
-общий простойкорень характеристического уравнения. Пусть 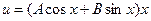 ,
,
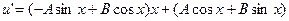
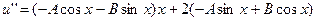 ,тогда, подставляя в исходное уравнение - получим
,тогда, подставляя в исходное уравнение - получим
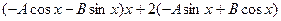 +
+ 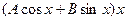 =
= 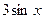
или 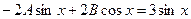 .
.
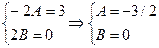 .Следовательно, общее решение данного уравнения имеет вид
.Следовательно, общее решение данного уравнения имеет вид
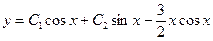
Постоянные 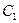 и
и 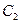 найдем, используя краевые условия.
найдем, используя краевые условия.
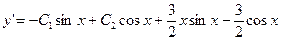
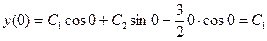
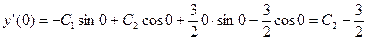
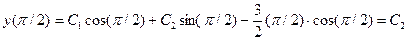
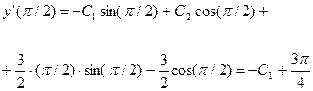
и, далее, 
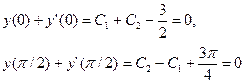
Таким образом , получим систему уравнений

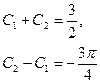 , решая которую,
, решая которую,
находим 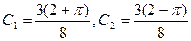 . Значит, решение исходного уравнения, удовлетворяющее поставленным краевым условиям, имеет вид
. Значит, решение исходного уравнения, удовлетворяющее поставленным краевым условиям, имеет вид