Геометрический смысл основных понятий
Дифференциальное уравнение  геометрически представляет собой поле направлений касательных к интегральным кривым.
геометрически представляет собой поле направлений касательных к интегральным кривым.
Общее решение – уравнение семейства интегральных кривых  , где параметр С=const .
, где параметр С=const .  )
)
Частное решение – уравнение интегральной кривой  семейства, проходящей через точку
семейства, проходящей через точку  .
.
Особые точки-точки плоскости, через которые либо проходит несколько интегральных кривых, либо не проходит ни одной.
Обыкновенные дифференциальные уравнения первого порядка с разделяющимися переменными.
Определение 3.1Дифференциальные уравнения первого порядка (2.2) и (2.3) называются уравнениями с разделяющимися переменными ,если они представимы в виде
 (3.1)
(3.1)
или
 (3.2).
(3.2).
В уравнениях (3.1) и (3.2) разделим переменные и проинтегрируем.
 или
или

 .
.
После интегрирования получим либо общий интеграл, либо общее решение.
Если заданы начальные условия  , то найдем частное решение, подставив С
, то найдем частное решение, подставив С  , найденное по начальным условиям, вместо С .
, найденное по начальным условиям, вместо С .
Пример 3.1
Решить задачу Коши  .
.
Решение:
 -это уравнение с разделяющимися переменными, т.к.
-это уравнение с разделяющимися переменными, т.к.  . Разделим переменные:
. Разделим переменные:  и проинтегрируем
и проинтегрируем
 или
или  - общий интеграл.
- общий интеграл.
Решим задачу Коши: В общий интеграл подставим начальные условия:1  -0
-0  =2С, С=
=2С, С=  . Запишем частный интеграл, подставив С=
. Запишем частный интеграл, подставив С=  в общий интеграл дифференциального уравнения.
в общий интеграл дифференциального уравнения.  - частный интеграл.
- частный интеграл.
Геометрический смысл дифференциального уравнения и его решений.
Геометрически решение данного дифференциального уравнения  представляет собой семейство равносторонних гипербол
представляет собой семейство равносторонних гипербол  , а частный интеграл, соответствующий решению задачи Коши
, а частный интеграл, соответствующий решению задачи Коши  - это гипербола
- это гипербола  , проходящая через заданную точку.(Рис.2)
, проходящая через заданную точку.(Рис.2)

Пример 3.2
Решить уравнение  .
.
Решение.
Разделим обе части уравнения на 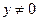 , получим уравнение с разделяющимися переменными
, получим уравнение с разделяющимися переменными  . Проинтегрируем это уравнение и получим
. Проинтегрируем это уравнение и получим  - общий интеграл дифференциального уравнения
- общий интеграл дифференциального уравнения  .
.
Потенцируя последнее равенство, получим общее решение уравнения  ,
,  .Заметим , что решение
.Заметим , что решение  входит в общее решение при С=0.
входит в общее решение при С=0.
К уравнениям с разделяющимися переменными приводятся уравнения вида  при помощи подстановки
при помощи подстановки  , где
, где  - постоянные.
- постоянные.
Подставим  в уравнение
в уравнение  .Получим
.Получим  , т.е.
, т.е.  . Проинтегрируем и получим
. Проинтегрируем и получим  . В общем интеграле вернемся к прежней переменной
. В общем интеграле вернемся к прежней переменной 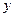 .
.
Пример 3.3.
Решить задачу Коши  .
.
Решение.
Пусть  , тогда
, тогда  , или
, или  . Разделим переменные и проинтегрируем
. Разделим переменные и проинтегрируем 
 .
.
Потенцируем полученное уравнение:  или
или  .
.
 - общее решение.
- общее решение.
Найдем частное решение:
 .
.
Подставим С в общее решение.  - частное решение.
- частное решение.
Задачи для самостоятельного решения
Найти общее (частное) решение уравнения
3.1.  .
.
3.2.  ,
,
3.3. 
3.4.  ;
;
3.5. 
Ответы:
3.1.  ;
;
3.2.  ;
;
3.3. 
3.4.  ;
;
3.5. 
