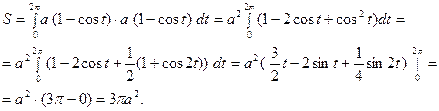Неопределённый интеграл
§ 1 ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Пусть функция 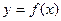 определена на некотором проме -жутке Х.
определена на некотором проме -жутке Х.
Определение 1. Функция 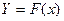 называется первооб –разной для функции
называется первооб –разной для функции 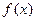 на промежутке Х, если для всех
на промежутке Х, если для всех 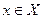 выполняется равенство
выполняется равенство 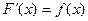 .
.
Так как производная постоянной равна 0 ( 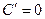 ), то любая функция вида
), то любая функция вида 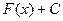 , где
, где 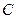 - произвольная постоянная, также является первообразной для функции
- произвольная постоянная, также является первообразной для функции 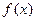 .
.
Определение 2. Множество всех первообразных функции 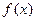 на промежутке
на промежутке 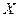 называется неопределённыминте - гралом и обозначается
называется неопределённыминте - гралом и обозначается 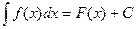 , где
, где 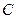 - произ -вольная постоянная.,
- произ -вольная постоянная., 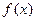 - подынтегральная функция ,
- подынтегральная функция , 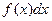 - подынтегральное выражение.
- подынтегральное выражение. 
Операция восстановления функции по её производной называется интегрированием.
СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. 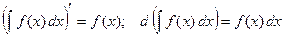 .
.
Благодаря этому свойству ( и в силу определения первообраз -ной), операцию интегрирования можно проверять дифференци -рованием.
2. 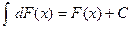 , в частности,
, в частности, 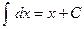 .
.
3. Постоянный множитель можно выносить за знак интеграла
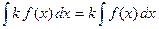 .
.
4. 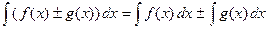 .
.
Используя то, что интегрирование - это операция обратная к операции дифференцирования, можем записать таблицу основных интегралов.
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1. 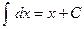 ;
;
2. 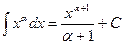 ,
, 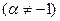 , в частности,
, в частности,
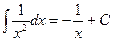 ,
, 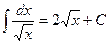 и т.д.
и т.д.
3. 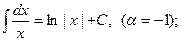
4. 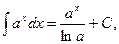 в частности,
в частности, 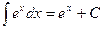 :
:
5. 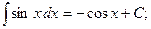 6.
6. 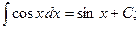
7. 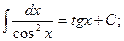 8.
8. 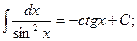
9. 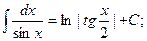 10.
10. 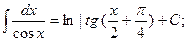
11. 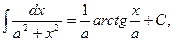 в частности,
в частности,
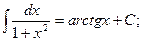
12. 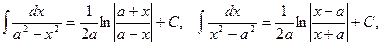 в частности,
в частности, 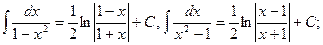
13. 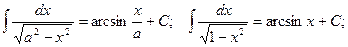
14. 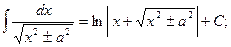 .
.
15. 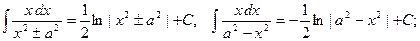
16. 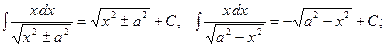
17. 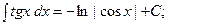
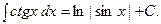
§ 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
1. НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ.
Метод сводится к тому, что при помощи тождественных
преобразований подынтегральной функции и при применении свойств неопределённого интеграла (3 и 4), связанных с алге- браическими операциями, вычисление интеграла сводится к применению табличных интегралов.
ПРИМЕРЫ.
1.
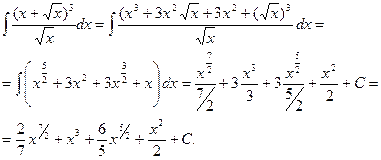
2. 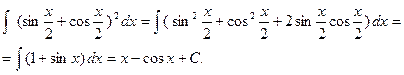
3.
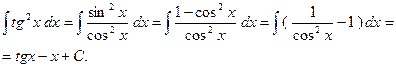
4.
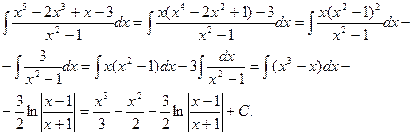
2. МЕТОД ПОДСТАНОВКИ ( ЗАМЕНЫ ПЕРЕМЕННОЙ В
НЕОПРЕДЕЛЁННОМ ИНТЕГРАЛЕ )
ТЕОРЕМА 1. Пусть функция 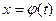 определена и диффе- ренцируема на некотором промежутке
определена и диффе- ренцируема на некотором промежутке 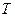 , а функция
, а функция 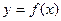 интегрируема на промежутке
интегрируема на промежутке 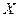 (области значений функции
(области значений функции 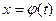 ). Тогда выполняется формула:
). Тогда выполняется формула:
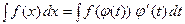 . (1)
. (1)
При этом, если вместо переменной  подставляется неко -торая функция (т.е. формула применяется «слева направо») то формула (1) называется формулой подстановки, а если, наоборот, вместо некоторой функции от
подставляется неко -торая функция (т.е. формула применяется «слева направо») то формула (1) называется формулой подстановки, а если, наоборот, вместо некоторой функции от  ставится некоторая новая переменная (т.е. формула действует «справа налево» ) то формула (1) называется формулой замены переменной в неопределённом интеграле..
ставится некоторая новая переменная (т.е. формула действует «справа налево» ) то формула (1) называется формулой замены переменной в неопределённом интеграле..
ПРИМЕРЫ.
1. 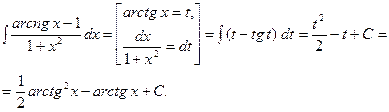
Замечание 1. После замены переменной или подстановки в неопределённом интеграле необходимо обязательно вернуться к исходной переменной.
2.
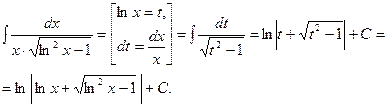
В этих примерах мы выполнили замену переменной, т.е. функцию заменили новой переменной. Теперь рассмотрим случай подстановки:
3. 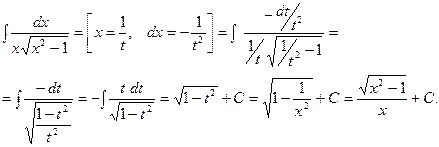 Рассмотрим следствия из формулы 1.
Рассмотрим следствия из формулы 1.
Следствие 1. Если 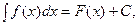 то
то
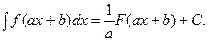
Например:
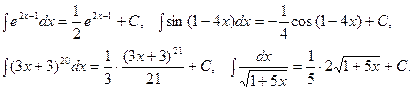
Следствие 2.
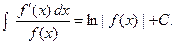
Например:
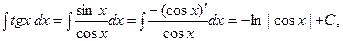 аналогично,
аналогично, 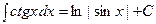 .
.
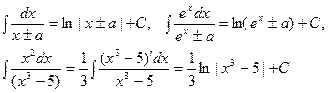
и так далее.
3. МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ.
Среди свойств неопределённого интеграла нет свойства ин -теграла от произведения двух функций. В некоторых случаях интеграл от произведения двух функций позволяет найти так называемая формула интегрирования по частям, которая по- лучается с использованием формулы производной произведе -ния двух функций. Если 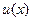 и
и 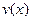 непрерывно дифференци- руемые функции на некотором промежутке
непрерывно дифференци- руемые функции на некотором промежутке 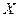 , то для этих функций может быть применена формула интегрирования по частям
, то для этих функций может быть применена формула интегрирования по частям
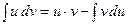 . (2)
. (2)
В самом деле,
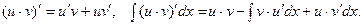
При использовании этого метода следует запомнить следующие правила:
1. Если под знаком интеграла стоят следующие функции : 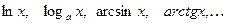 , которые исчезают после дифференцирования, то эти функции обозначают через
, которые исчезают после дифференцирования, то эти функции обозначают через 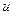 , а всё остальное выражение в интеграле - через
, а всё остальное выражение в интеграле - через 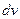 .
.
2. Если под знаком интеграла, стоят функции, которые не исчезают после вычисления производной
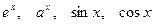 и т. д.,
и т. д.,
то эти функции вместе с 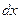 обозначают через
обозначают через 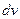 , а
, а
остальные выражения, которые стоят под знаком инте-
грала, - через 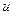 .
.
Рассмотрим несколько примеров.
1. 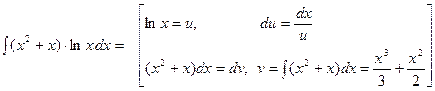
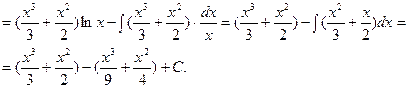
2. 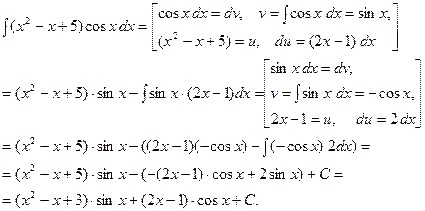
3.
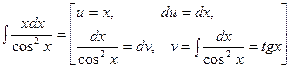 =
=
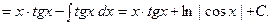
Таким образом, в качестве 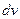 мы можем выбирать функцию, от которой хорошо вычисляется интеграл, а в качестве
мы можем выбирать функцию, от которой хорошо вычисляется интеграл, а в качестве 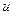 - ту функцию или выражение, которые исчезает после дифференцирования.
- ту функцию или выражение, которые исчезает после дифференцирования.
§ 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
Определение 1. Дробно – рациональной функцией (или просто рациональной дробью) называется выражение вида
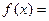
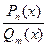 , где
, где 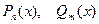 - многочлены степени
- многочлены степени 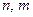 , соответ –ственно. Если
, соответ –ственно. Если 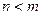 , дробь называется правильной. Если же
, дробь называется правильной. Если же 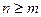 , то дробь называется неправильной. Любую непра -вильную дробь, после деления «уголком» можно представить в виде
, то дробь называется неправильной. Любую непра -вильную дробь, после деления «уголком» можно представить в виде
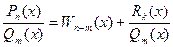 , где
, где 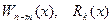 - многочлены, причём
- многочлены, причём 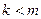 .
.
Например, 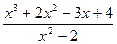 - неправильная рациональная дробь. Разделим числитель на знаменатель «уголком»:
- неправильная рациональная дробь. Разделим числитель на знаменатель «уголком»:
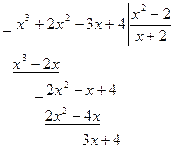
Тогда
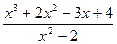 =
= 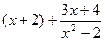 .
.
Любую правильную рациональную дробь можно с помощью метода неопределённых коэффициентов, представить в виде суммы простейших рациональных дробей. Они бывают четы-: рёх типов:
1. 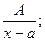 2.
2. 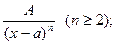 3.
3. 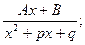
4. 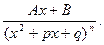 ( Здесь
( Здесь 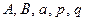 - некоторые дейст -вительные числа, а квадратный трёхчлен
- некоторые дейст -вительные числа, а квадратный трёхчлен 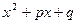 не имеет действительных корней ).
не имеет действительных корней ).
Для дробей 1 – го и 2 - го типа выполняются формулы: 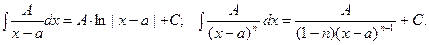 Вычисление интегралов 3 – его типа рассмотрим на приме –рах:
Вычисление интегралов 3 – его типа рассмотрим на приме –рах:
1. 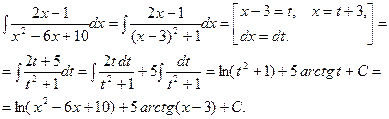
2.
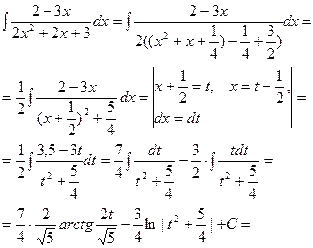
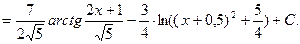
Такой же метод можно применить и в случае, если квад -ратный трёхчлен в знаменателе имеет неотрицательный дискриминант. В самом деле
3.
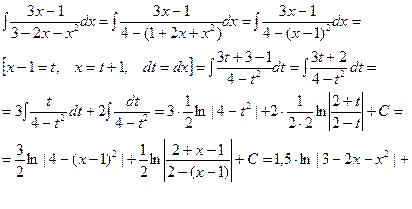
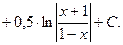
Рассмотрим теперь несколько примеров, в которых, инте- грал вычисляется разложением подынтегральной функции на простейшие дроби методом неопределённых коэффициентов.
Сначала рассмотрим самый простой случай, когда зна -менатель рациональной дроби представляет собой произве -дение нескольких различных линейных скобок :
4.
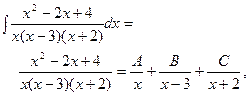
после умножения последнего равенства на общий знаменатель, получим:
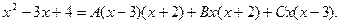
Данное равенство должно выполняться для всех значений  . Поэтому, при
. Поэтому, при 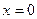 получим
получим 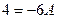 или
или 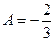 ; при
; при 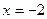 получается
получается 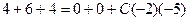 ,
, 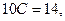 или
или 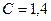 ; при
; при 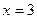 имеем
имеем 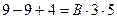 , отсюда
, отсюда 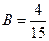 . Тогда, возвращаясь к интегралу, получим,
. Тогда, возвращаясь к интегралу, получим,
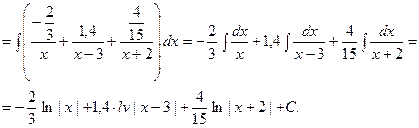
Сложнее получается, если знаменатель рациональной дро -би имеет кратные корни, т.е. содержит множитель вида 
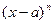 . В этом случае при разложении дроби на прос -тейшие следует запомнить, что каждой скобке вида
. В этом случае при разложении дроби на прос -тейшие следует запомнить, что каждой скобке вида 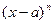 Отвечает не одно, а
Отвечает не одно, а 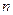 , слагаемых, т.е. в разложении при -сутствуют все степени данной скобки. Рассмотрим пример:
, слагаемых, т.е. в разложении при -сутствуют все степени данной скобки. Рассмотрим пример:
5. 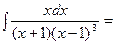
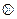
Подынтегральную функцию представим в виде суммы простейших дробей:
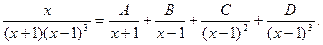
Умножим данное равенство на общий знаменатель. Получим:
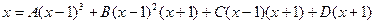 .
.
Раскроем все скобки:
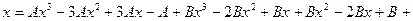
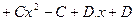
Приравняем коэффициенты при одинаковых степенях  :
:
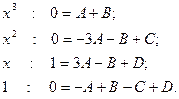
Получили систему четырёх уравнений с четырьмя неиз- вестными. Можем решить эту систему методом исключения: 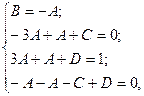 или
или 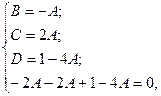
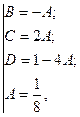 следовательно
следовательно 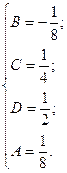
 Возвращаемся к интегралу:
Возвращаемся к интегралу:
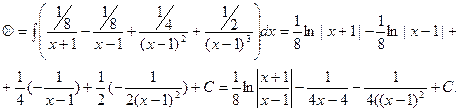 Метод нахождения коэффициентов, который мы использова-ли в данном примере, называется «методом неопределённых коэффициентов».
Метод нахождения коэффициентов, который мы использова-ли в данном примере, называется «методом неопределённых коэффициентов».
Рассмотрим теперь более общий пример.
6.
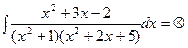 .
.
Разложим подынтегральную функцию на элементарные дроби:
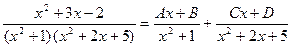
(скобки в знаменателе не имеют действительных корней, поэ- тому в разложении появились дроби 3–го типа). Умножив дан- ное равенство на общий знаменатель, получим:
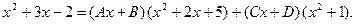
Раскроем скобки: 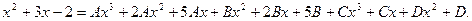 Приравняем коэффициенты при одинаковых степенях
Приравняем коэффициенты при одинаковых степенях  :
:
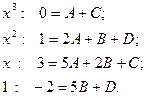
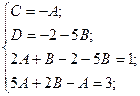
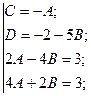
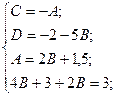
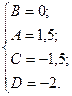
Тогда получим следующий интеграл:
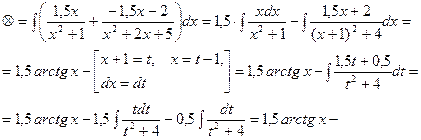
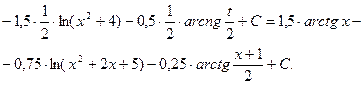
§ 4. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
1. Самый простой случай, если подынтегральная функция
содержит произведение синусов и косинусов разных аргу -ментов. В этом случае используют обычные формулы пре -образования произведения тригонометрических функций в сумму:
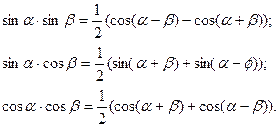
Например:
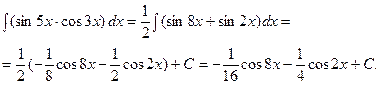
2. Интегралы вида 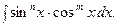
1). Если  и нечётное, то
и нечётное, то 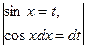 . Например,
. Например,
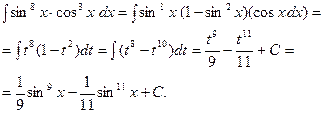
2). Если 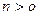 и нечётное, то
и нечётное, то 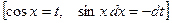 , например:
, например:
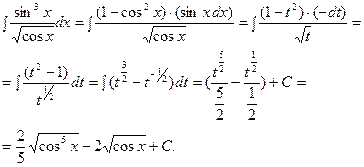
3). Если и 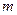 и
и 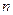 - чётные, то при вычислении интеграла следует использовать формулы понижения степени:
- чётные, то при вычислении интеграла следует использовать формулы понижения степени:
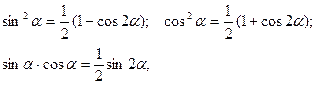
Например, 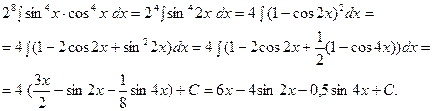
4) Если 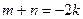 ( чётная и отрицательная ), то приме -няется замена:
( чётная и отрицательная ), то приме -няется замена:
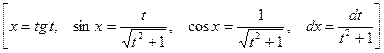 .
.
Рассмотрим пример:
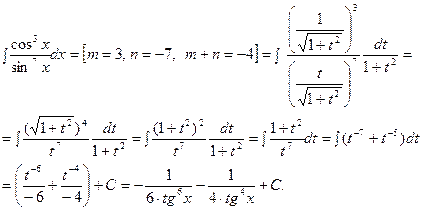
3. Интегралы вида 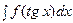 или приводящиеся к такому виду: замена
или приводящиеся к такому виду: замена 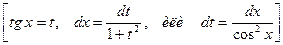 . Рассмотрим соответствующие примеры:
. Рассмотрим соответствующие примеры:
1) 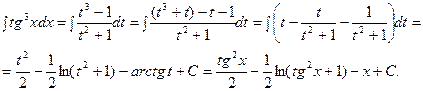
2) 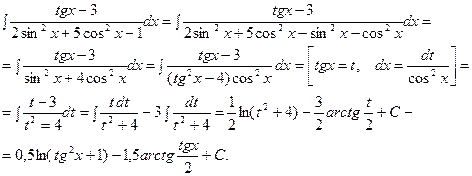
4. Универсальная тригонометрическая подстановка:
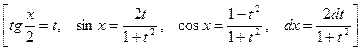
применяется, если мы имеем интеграл вида 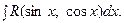 Например,
Например,
1.
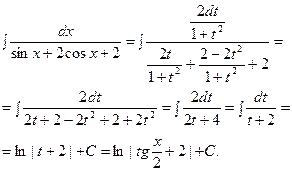
2.
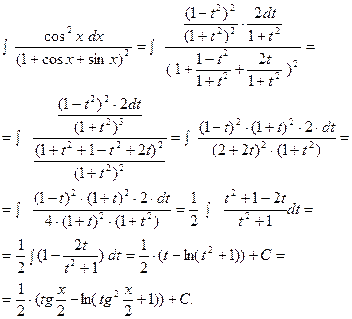
Замечание. Так как применение универсальной тригоно -метрической подстановки зачастую приводит к громоздким рациональным выражениям, то применять её рекомендуется в тех случаях, когда другие подстановки «не работают».
§ 5. ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ.
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
1. Если подынтегральная функция состоит из одного или нескольких корней разных порядков от одного и того же линейного выражения, то подкоренное выражение заменяем таким образом, чтобы избавиться от всех корней сразу, т.е. заменяем через 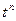 , где
, где 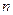 - наименьшее общее кратное всех порядков корней. Например: а)
- наименьшее общее кратное всех порядков корней. Например: а)
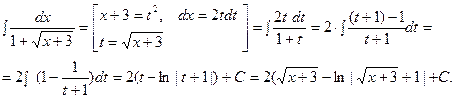 б)
б)
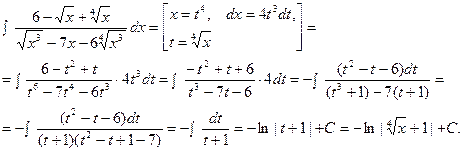
2. Интеграл вида 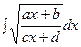 . Рассмотрим пример:
. Рассмотрим пример:
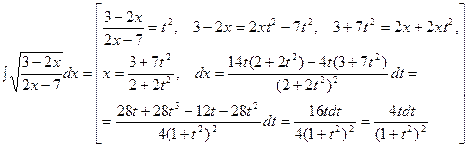
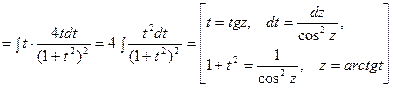
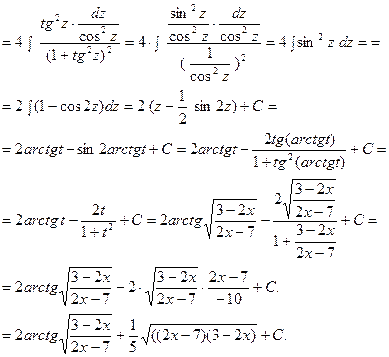
3. Интеграл вида 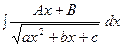 . Следует выделить полный квадрат в подкоренном выражении и сделать соответ- ствующую замену переменной. Например:
. Следует выделить полный квадрат в подкоренном выражении и сделать соответ- ствующую замену переменной. Например:
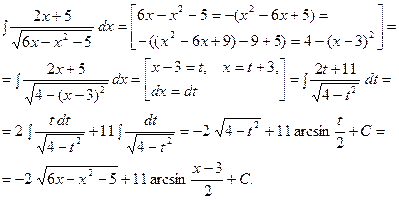
4. Тригонометрические подстановки:
А. 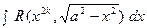 . Применяется подстановка:
. Применяется подстановка:
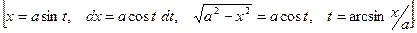
Например,
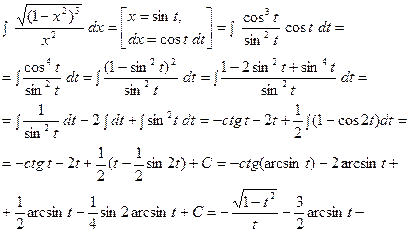
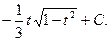
В. Интеграл вида 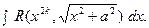 При вычислении таких интегралов используется подстановка:
При вычислении таких интегралов используется подстановка:
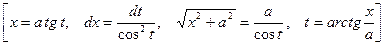 .
.
Например:
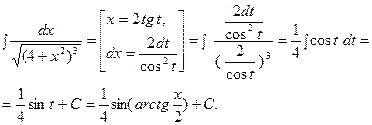
С. Интеграл вида 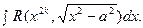 Подстановка:
Подстановка:
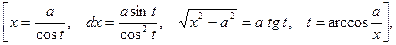 например:
например: 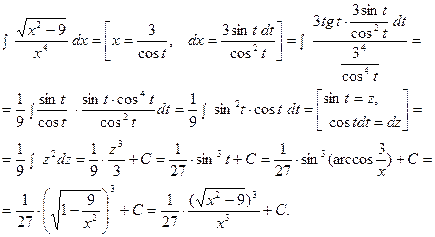 Замечание. Тригонометрические подстановки целесообраз -но применять в том случае, если подынтегральная функция содержит только чётные степени
Замечание. Тригонометрические подстановки целесообраз -но применять в том случае, если подынтегральная функция содержит только чётные степени  .
.
Мы рассмотрели основные приёмы интегрирования функций. Следует заметить, что интегрирование какой - либо функции может выполняться разными способами.. Правильный выбор метода интегрирования позволяет ускорить выполнение задачи. Фактически очень многое зависит от сообразительности и навыков, получаемых в результате тренировки.
Но не всегда удаётся найти первообразную в виде эле -ментарной функции. Существует класс функций, для которых интеграл не выражается через элементарные функции (т.е. так называемые «не берущиеся» интегралы), но которые имеют большое значение в приложениях, например 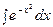 - инте -грал Пуассона - применяется в теории вероятностей;
- инте -грал Пуассона - применяется в теории вероятностей; 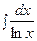 - интегральный логарифм - применяется в теории чисел;
- интегральный логарифм - применяется в теории чисел;
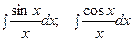 - интегральные синус и косинус;
- интегральные синус и косинус; 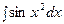 ,
, 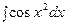 - интегралы Френеля - используются в физике, и т.д.
- интегралы Френеля - используются в физике, и т.д.
2. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
§ 1 . ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И СВОЙСТВА.
Пусть функция 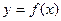 определена и на отрезке
определена и на отрезке 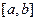 . Разделим этот отрезок на
. Разделим этот отрезок на 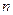 частей точками:
частей точками: 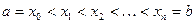 . На каждом элементарном отрез- ке выберем произвольную точку
. На каждом элементарном отрез- ке выберем произвольную точку 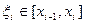 . Длину элемен -тарного отрезка обозначим
. Длину элемен -тарного отрезка обозначим 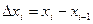 . Пусть
. Пусть 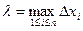 . Составим сумму
. Составим сумму
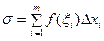 . (1)
. (1)
Эта сумма называется интегральной суммой для функции 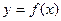 на отрезке
на отрезке 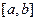 . Если существует конечный предел этой суммы при
. Если существует конечный предел этой суммы при 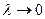 , то этот предел называется опреде-лённым интегралом от функции
, то этот предел называется опреде-лённым интегралом от функции 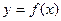 на отрезке
на отрезке 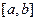 и обозначается
и обозначается
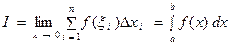 . (2)
. (2)
Если функция 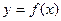 непрерывная на отрезке
непрерывная на отрезке 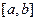 , то предел интегральной суммы существует и не зависит от спо -соба разбиения отрезка
, то предел интегральной суммы существует и не зависит от спо -соба разбиения отрезка 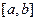 и выбора точек
и выбора точек 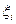 . Числа
. Числа 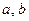 называются соответственно нижним и верхним пределами ин –тегрирования.
называются соответственно нижним и верхним пределами ин –тегрирования.
Если 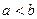 и
и 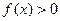 на
на 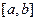 , то определённый инте -грал представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции
, то определённый инте -грал представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции 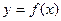 , с боковых сторон прямыми
, с боковых сторон прямыми 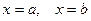 , а снизу - осью
, а снизу - осью 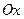 . (Геометрический смысл определённого интеграла).
. (Геометрический смысл определённого интеграла).
СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА:
1. 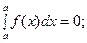 2.
2. 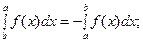
3. для любых точек 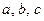 выполняется равенство
выполняется равенство
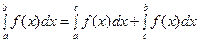 ;
;
4. 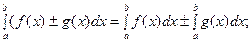
5. 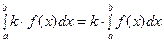 ; (
; ( 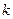 - постоянный множитель):
- постоянный множитель):
6. Если для всех 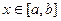 выполняется неравенство:
выполняется неравенство:
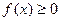 , то
, то 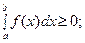
7. Если для всех 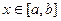 выполняется неравенство:
выполняется неравенство:
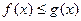 , то для интеграла выполняется анало –
, то для интеграла выполняется анало –
гичное неравенство: 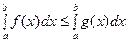 :
:
8. Если 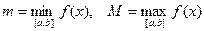 , т.е. для всех
, т.е. для всех 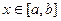 выполняется неравенство
выполняется неравенство 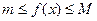 ,
,
то 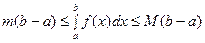 ;
;
9. (Формула среднего значения) Если функция 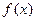 не- прерывна на отрезке
не- прерывна на отрезке 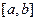 , то на этом отрезке существует точка
, то на этом отрезке существует точка 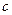 такая, что
такая, что
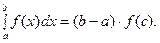
Замечание. Формула среднего значения имеет простой геометрический смысл: величина определённого интеграла при 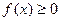 численно равна площади прямоугольника, имеющего высоту
численно равна площади прямоугольника, имеющего высоту 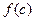 и основание - отрезок длины
и основание - отрезок длины 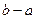 .
.
§ 2. ПРАВИЛА ВЫЧИСЛЕНИЯ ОПРЕДЕЛЁННОГО
ИНТЕГРАЛА.
1. Формула Ньютона – Лейбница.
Если функция 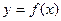 непрерывна на отрезке
непрерывна на отрезке 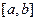 и
и 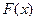 какая – либо её первообразная на
какая – либо её первообразная на 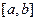 , то имеет место формула, которая называется формулой Ньютона – Лейбница:
, то имеет место формула, которая называется формулой Ньютона – Лейбница:
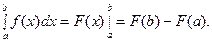
ПРИМЕРЫ:
1. 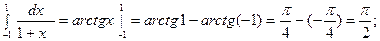
2. 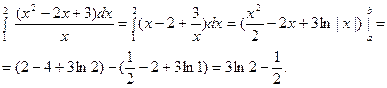
2. Замена переменной в определённом интеграле.
Пусть 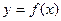 - непрерывная функция на отрезке
- непрерывная функция на отрезке 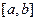 , а функция
, а функция 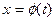 непрерывна и дифференцируема на от –резке
непрерывна и дифференцируема на от –резке 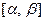 таком, что
таком, что 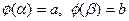 . Тогда справедлива формула:
. Тогда справедлива формула:
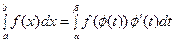 .
.
Если применяем эту формулу «слева – направо» - то это формула подстановки (т.е. вместо  подставляем некоторую функцию, а если в другую сторону(т.е. некоторую функцию заменяем новой переменной, то это формула замены пере- менной в определённом интеграле.
подставляем некоторую функцию, а если в другую сторону(т.е. некоторую функцию заменяем новой переменной, то это формула замены пере- менной в определённом интеграле.
При выполнении замены переменной или подстановки ис -пользуются те же методы, что и при вычислении неопреде -лённого интеграла. Следует только иметь ввиду следующее замечание.
ЗАМЕЧАНИЕ. После замены переменной в определённом интеграле нет необходимости возвращаться к исходной пере- меной. Требуется только изменить пределы интегрирования в соответствии с заменой, т.е определить границы изменения новой переменной.
ПРИМЕРЫ
1.
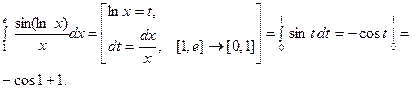
2.
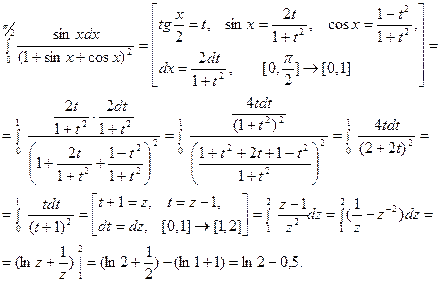 3.
3.
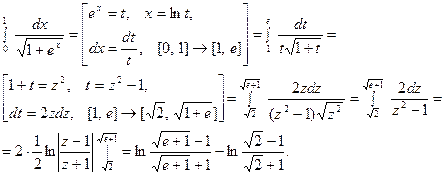
В этих примерах мы заменяли функцию некоторой пере -менной. Теперь рассмотрим случаи подстановки.
4.
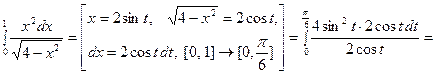
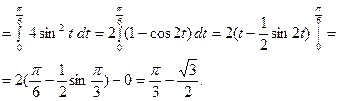
5.
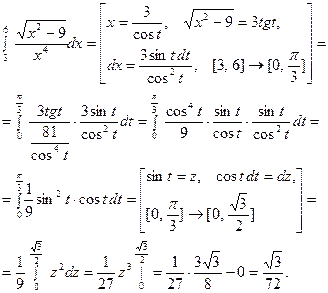
3. Интегрирование «по частям» в определённом интеграле.
Если функции 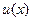 и
и 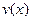 имеют непрерывные произ – водные на отрезке
имеют непрерывные произ – водные на отрезке 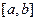 , то справедлива формула:
, то справедлива формула:
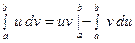 .
.
Правила выбора замены функций через 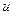 и
и 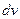 такие же, как для неопределённого интеграла.
такие же, как для неопределённого интеграла.
Рассмотрим несколько примеров:
1. 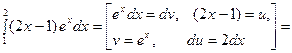
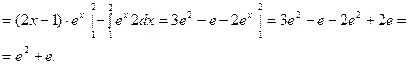
2.
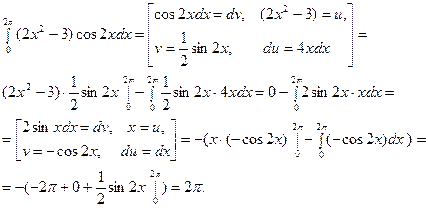
3.
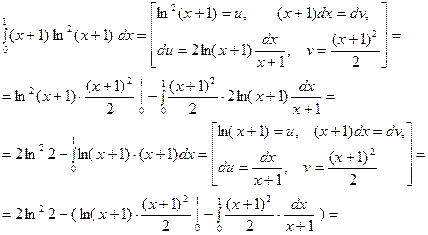
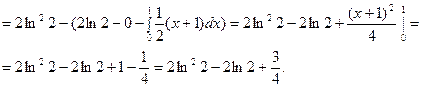
§ 3. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
1. Площадь криволинейной трапеции. (из геометри- ческого смысла определённого интеграла):
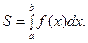 (1)
(1)
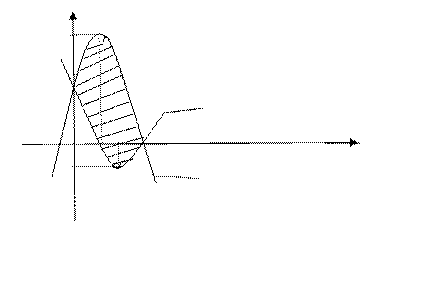
ПРИМЕР 1. Найти площадь фигуры, ограниченной линиями: 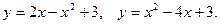 Это две параболы. Вершина первой в точке (1, 4), ветви направлены вниз; вершина второй в точке (2, -1), ветви направлены вверх.
Это две параболы. Вершина первой в точке (1, 4), ветви направлены вниз; вершина второй в точке (2, -1), ветви направлены вверх.
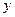

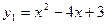
1 2 3 
О
-1
Площадь заштрихованной фигуры можно найти по формуле:
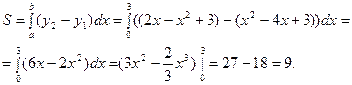
2. Найти площадь фигуры, ограниченной линиями:
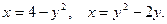

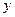
 |

 2
2
 |

 -1 0 4
-1 0 4 
-1

Найдём точки пересечения линий 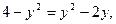
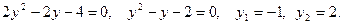 Площадь находим по формуле:
Площадь находим по формуле: 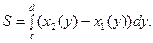
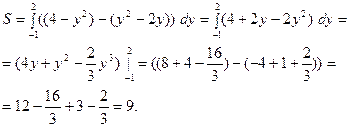
ЗАМЕЧАНИЕ Для вычисления площади криволинейной тра -пеции в случае, когда верхняя граница задана параметричес -кими уравнениями 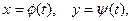 причём
причём 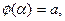
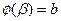 , то в формуле (1) необходимо сделать замену переменной, положив
, то в формуле (1) необходимо сделать замену переменной, положив 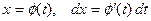 . Получим:
. Получим:
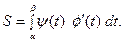 (2)
(2)
Например, найти площадь одной арки циклоиды:
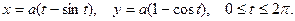

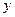
 2
2 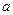
 |

О