Формулы для площади треугольника

Формулы, позволяющие находить площадь треугольника, удобно представить в виде следующей таблицы.

Фигура	Рисунок	Формула площади	Обозначения
Произвольный треугольник		Посмотреть вывод формулы	a – любая сторона, ha – высота, опущенная на эту сторону
	Посмотреть вывод формулы	a и b – две любые стороны, С – угол между ними
	. Посмотреть вывод формулы Герона	a, b, c – стороны, p – полупериметр, формулу называют «Формула Герона»

Равносторонний (правильный) треугольник

Посмотреть вывод формулы

a – сторона

Теорема о высоте прямоугольного треугольника

Если высота длиной 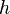, проведённая из вершины прямого угла, делит гипотенузу длиной на отрезк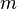и и , соответствующие катетам 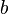и 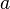, то верны следующие равенства:

• 
• ;
• 

Параллелограмм

Материал из Википедии — свободной энциклопедии

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства

• Противоположные стороны параллелограмма равны.

.

• Противоположные углы параллелограмма равны.

• Диагонали параллелограмма пересекаются и точка пересечения делит их пополам.

.

• Сумма углов, прилежащих к одной стороне, равна 180°( по признаку параллельных прямых).

Площадь параллелограмма

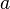, где — сторона, 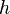— высота, проведенная к этой стороне.

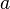, где и 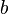— стороны, а — угол между сторонами a и b.

Ромб

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 марта 2014; проверки требует 1 правка.

У этого термина существуют и другие значения, см. Ромб (значения).

Ромб (др.-греч. ῥόμβος, лат. rombus «бубен») — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом.

Свойства

1. Ромб является параллелограммом. Его противолежащие стороны равны и попарно параллельны, АВ || CD, AD || ВС.
2. Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам.
3. Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).

Площадь ромба

• Площадь ромба равна половине произведения его диагоналей.

• Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.

• Кроме того, площадь ромба может быть вычислена по формуле:

,

Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора.

Для плоского треугольника со сторонами и углом , противолежащим стороне 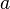, справедливо соотношение: . Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними[1]

Теоре́ма си́нусов — теорема, устанавливающая зависимость между сторонами треугольника и противолежащими им углами. Существуют два варианта теоремы; обычная теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

и расширенная теорема синусов

Для произвольного треугольника где 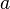, , 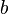— стороны треугольника, — соответственно противолежащие им углы, а — радиус окружности, описанной вокруг треугольника.

Трапеция

Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только пара сторон параллельна . Две параллельные стороны называются основаниями трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции.

Равнобедренная трапеция

Прямоугольная трапеция

Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой

• Параллельные стороны называются основаниями трапеции.
• Две другие стороны называются боковыми сторонами.
• Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Виды трапеций

• Трапеция, у которой боковые стороны равны, называется равнобокой, равнобочной или равнобедренной трапецией.
• Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Общие свойства