Синус, косинус и тангенс острого угла прямоугольного треугольника
Основные линии треугольника
Медиана
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
- Медиана разбивает треугольник на два треугольника одинаковой площади.
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
- Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Биссектриса
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Высота
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства высот треугольника
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Срединный перпендикуляр
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Средняя линия
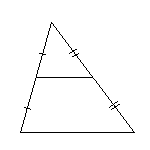Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя — основанием.
Свойства
- Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.
- Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой.
Типы треугольников
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Свойства
Далее предполагаем, что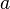 
и 
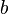длины катетов, а 
длина гипотенузы
- (Теорема Пифагора)
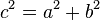
- Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
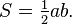
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 
. Другими словами, половина развернутого угла.
Острый угол — меньший .
Тупой угол — больший . Применительно к такому углу «тупой» — не оскорбление, а математический термин :-)
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается 
. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается 
.
Угол 
обозначается соответствующей греческой буквой 
.
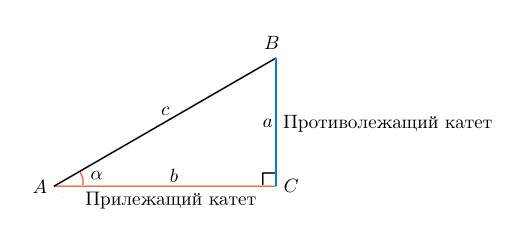
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет 
, который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
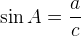
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
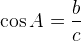
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Площадь треугольника