Требования к математическим моделям

Математические модели (ММ) служат для описания свойств объектов в процедурах АП. Если проектная процедура включает создание ММ и оперирование ею с целью получения полезной информации об объекте, то говорят, что процедура выполняется на основе математического моделирования.

К математическим моделям предъявляются требования универсальности, адекватности, точности и экономичности.

Степень универсальности ММ характеризует полноту отображения в модели свойств реального объекта. Математическая модель отражает лишь некоторые свойства объекта.

Точность ММ оценивается степенью совпадения значений параметров реального объекта и значений тех же параметров, рассчитанных с помощью оцениваемой ММ. Пусть отражаемые в ММ свойства оцениваются вектором выходных параметров Y = (y₁, y₂, ..., y_m). Тогда, обозначив истинное и рассчитанное с помощью ММ значения j-го параметра через y_jист и y_jm соответственно, определим относительную погрешность E_j расчета параметра Y_j как

E_j = (y_jm - y_jист)/y_jист (2.1)

Получена векторная оценка Е = (E₁, E₂, ..., E_m). При необходимости сведения этой оценки к скалярной используют какую-либо норму вектора Е, например

E_m = ||E|| = maxE_j.

j O [1m]

Адекватность ММ - способность отражать заданные свойства объекта с погрешностью не выше заданной. Поскольку выходные параметры являются функциями векторов параметров внешних Q и внутренних Х, погрешность E_j зависит от значений Q и Х.

Обычно значения внутренних параметров ММ определяют из условия минимизации погрешности E_м в некоторой точке Q_ном пространства внешних переменных, а используют модель с рассчитанным вектором при различных значениях Q. При этом, как правило, адекватность модели имеет место лишь в ограниченной области изменения внешних переменных - области адекватности (АО) математической модели:

OA = {Q|E_m, d},

где d - заданная константа, равная предельно допустимой погрешности модели.

Экономичность ММ характеризуется затратами вычислительных ресурсов. Чем они меньше, тем модель экономичнее.

2.3.2.

Классификация математических моделей

Рассмотрим основные признаки, классификации и типы ММ, применяемые в САПР.

По характеру отображаемых свойств объекта ММ делятся на структурные и функциональные.

Структурные ММ предназначены для отображения структурных свойств объекта. Различают структурные ММ топологические и геометрические.

В топологических ММ отображаются состав и взаимосвязи элементов. Их чаще всего применяют для описания объектов, состоящих из большого числа элементов, при решении задач привязки конструктивных элементов к определенным пространственным позициям (например, задачи компоновки оборудования, размещения деталей, трассировки соединений) или к относительным моментам времени (например, при разработке расписаний, технологических процессов). Топологические модели могут иметь форму графов, таблиц (матриц), списков и т.п.

В геометрических ММ отображаются свойства объектов, в них дополнительно к сведениям о взаимном расположении элементов содержатся сведения о форме деталей. Геометрические ММ могут выражаться совокупностью уравнений линий и поверхностей; совокупностью алгебраических соотношений, описывающих области, составляющие тело объекта; графами и списками, отображающими конструкции из типовых конструктивных элементов, и т.п. Геометрические ММ применяют при решении задач конструирования в машиностроении, приборостроении, радиоэлектронике, для оформления конструкторской документации, при задании исходных данных на разработку технологических процессов изготовления деталей. Используют несколько типов геометрических ММ.

Функциональные ММ предназначены для отображения физических или информационных процессов, протекающих в объекте при его функционировании или изготовлении. Обычно функциональные ММ представляют собой системы уравнений, связывающих фазовые переменные, внутренние, внешние и выходные параметры.

По степени детализации описания в пределах каждого иерархического уровня выделяют полные ММ и макромодели.

Полная модель - эта модель, в которой фигурируют фазовые переменные, характеризующие состояния всех имеющихся межэлементных связей (т.е. состояние всех элементов проектируемого объекта).

Макромодель - ММ, в которой отображаются состояния значительно меньшего числа межэлементных связей, что соответствует описанию объекта при укрупненном выделении элементов.

По способу представления свойств объекта функциональные ММ делятся на аналитические и алгоритмические.

Аналитические ММ представляют собой явные выражения выходных параметров как функций входных и внутренних параметров.

Алгоритмические ММ выражают связи выходных параметров с параметрами внутренними и внешними в форме алгоритма.

Имитационная ММ - это алгоритмическая модель, отражающая поведение исследуемого объекта во времени при задании внешних воздействий на объект.

2.3.3.

Математические модели на микро-, макро- и метауровнях

Описания технических объектов должны быть по сложности согласованы с возможностями восприятия человеком и с возможностями ЭВМ оперировать описаниями моделей в процессе их преобразования при проектировании. Однако выполнить это требование в рамках некоторого единого описания, не расчленяя его на отдельные составные части, удается лишь для простых изделий. Как правило, требуется структурирование описаний и соответствующее расчленение представлений о проектируемых объектах на иерархические уровни и аспекты. Это позволяет распределять работы по проектированию сложных объектов между подразделениями проектной организации, что способствует эффективности и производительности труда проектировщиков.

Использование принципов блочно-иерархического подхода к проектированию структур математических моделей проектируемых объектов позволяет формализовать процесс их написания. Количество иерархических уровней при моделировании определяется сложностью проектируемых объектов и возможностью средств проектирования. Однако иерархические уровни большинства предметных областей можно отнести к одному из трех обобщенных уровней, называемых далее микро-, макро- и метауровнями.

В зависимости от места в иерархии описания математические модели делятся на ММ, относящиеся к микро-, макро- и метауровням.

Особенностью ММ на микроуровне является отражение физических процессов, протекающих в непрерывном пространстве и времени. Типичные ММ на микроуровне - дифференциальные уравнения в частных производных (ДУЧП). В них независимыми переменными являются пространственные координаты и время. С помощью этих уравнений рассчитываются поля механических напряжений и деформаций, электрические потенциалы и напряжения, давления и температуры и т.п. Возможности применения ММ в ДУЧП ограничены отдельными деталями, попытки анализировать с их помощью процессы в многокомпонентных средах, сборочных единицах, электронных схемах не могут быть успешными из-за чрезмерного роста затрат машинного времени и памяти.

На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде систем обыкновенных дифференциальных уравнений (ОДУ). В этих уравнениях независимой переменной является время t, а вектор зависимых переменных составляют фазовые переменные, характеризующие состояние укрупненных элементов дискретизированного пространства. Такими переменными являются силы и скорости в механических системах, напряжения и токи в электрических системах, давления и расходы жидкостей и газов в гидравлических и пневматических системах и т.п. Системы ОДУ являются универсальными моделями на макроуровне, пригодными для анализа как динамических, так и установившихся состояний объектов. Модели для установившихся режимов можно также представить в виде систем алгебраических уравнений. Порядок системы уравнений зависит от числа выделенных элементов объекта. Если порядок системы приближается к 10000, то оперирование моделью становится затруднительным и поэтому необходимо переходить к представлениям на метауровне.

На метауровне в качестве элементов принимают достаточно сложные совокупности деталей. Метауровень характеризуется большим разнообразием типов используемых ММ. Для многих объектов ММ на метауровне по-прежнему представляются системами ОДУ. Однако так как в моделях не описываются внутренние фазовые переменные элементы, а фигурируют только фазовые переменные, относящиеся к взаимным связям элементов, укрупненное представление элементов на метауровне означает получение ММ приемлемой размерности для существенно более сложных объектов, чем размерность ММ на макроуровне.

В ряде предметных областей удается использовать специфические особенности функционирования объектов для упрощения ММ. Примером являются электронные устройства цифровой автоматики, в которых возможно применять дискретное представление таких фазовых переменных, как напряжения и токи. В результате ММ становится системой логических уравнений, описывающих процессы преобразования сигналов. Такие логические модели существенно более экономичны, чем модели электрические, описывающие изменения напряжений и токов как непрерывных функций времени.

Применение тензорных представлений об объектах проектирования дает возможность использовать для получения ММ сложных технических систем методы диакоптики.

Исследование сложных систем по частям реализуется в диакоптических методах исследования. Отличие диакоптического подхода проектирования от блочно-иерархического заключается в том, что диакоптика основана на использовании структурных особенностей анализируемых схем и выражающих их матриц, а не на принятии каких-либо упрощающих допущений. В диакоптических методах производится расчленение математических моделей на части, исследуемые самостоятельно.

Расчленение математических моделей на части позволяет упорядочить и минимизировать количество обменов информацией между оперативной и внешней памятью при анализе сложных систем, а также выбирать для исследования каждой части наиболее выгодные режимы анализа. Эти обстоятельства делают диакоптические методы экономичными по затратам машинных времени и оперативной памяти.

Макромоделирование лежит в основе направления, связанного с рациональным выбором математических моделей элементов при построении математической модели системы. Макромоделирование реализует возможность использования при анализе одного и того же объекта нескольких моделей, различающихся сложностью, точностью и полнотой отображения свойств объекта, трудоемко-стью требующихся вычислений и т.п.

При макромоделировании должны выполняться условия:

· адекватности модели (выполнение данного условия требует от инженера учета целей решения каждой конкретной задачи и степени влияния параметров выделяемых элементов на результаты решения этой задачи);

· большей экономичности создания макромоделей элементов и их дальнейшего использования по сравнению с решением задачи на основе полной математической модели (обычно это условие выполняется при использовании макромоделей для элементов типовых или, по крайней мере, часто встречающихся в данной системе);

Событийность анализа заключается в том, что при имитации процессов, протекающих в исследуемом объекте, в каждый момент модельного времени вычисления проводятся только для небольшой части математической модели объекта. Эта часть включает в себя те элементы, состояние которых на очередном временном шаге может измениться. Использование принципа событийности существенно повышает экономичность анализа на функционально-логическом и системном уровнях проектирования.

Рациональное использования эвристических способностей человека в интерактивных процедурах позволяет инженеру вмешиваться в ход вычислений и выбирать наиболее перспективные продолжения на основе эвристических оценок. Это выгодно во всех тех проектных процедурах, в которых следование только формальным критериям выбора дальнейших действий связано с чрезмерными затратами машинного времени. При исследовании сложных элементов и устройств автоматизации часто используют методы многовариантного анализа и теорию чувствительности.

Основными видами многовариантного анализа в задачах проектирования являются анализы чувствительности и статистический.

Цель анализа чувствительности - определение коэффициентов чувствительности, называемых также коэффициентами влияния:

a_ji = δY_i/δx_i ; b_ji = a_jix_iном/Y_iном (2.1)

где a_ji и b_ji - абсолютный и относительный коэффициенты чувствительности выходного параметра y_j к изменениям внутреннего параметра X_i; y_iном и x_iном - номинальные значения параметров y_j и X_i. Результаты анализа чувствительности m выходных параметров к изменениям n внутренних параметров представляют собой mn коэффициентов чувствительности, составляющих матрицу абсолютной или относительной чувствительности.

Анализ чувствительности применяется, если параметры Х и Q можно считать непрерывными величинами, а параметры y_j являются дифференцируемыми функциями своих аргументов X_i и q_kном.

Результаты анализа чувствительности используются при решении таких важных задач, как параметрическая оптимизация, расчет допусков, оценка точности выходных параметров. Именно по значениям коэффициентов чувствительности разработчик отделяет существенно влияющие параметры от мало влияющих, определяет направления изменений внутренних параметров для улучшения выходных параметров, оценивает допустимые отклонения параметров Х и Q для выполнения точностных требований к параметрам Y.

В ряде случаев для получения результатов математических экспериментов используют метод приращений. Это основной метод анализа чувствительности в инвариантном МО САПР. Метод

· приращений есть метод численного дифференцирования зависимости

Y = F(X, Q).

Алгоритм метода приращений включает в себя (n + 1)-кратное обращение к модели для вычисления Y, где n - количество варьируемых параметров, т.е. таких параметров (или q_k), влияние которых на Y исследуется. В первом варианте задаются номинальные значения аргументов и, следовательно, результатом обращения к модели будет номинальное значение Y_ном = (Y_1ном,Y_2ном, ..., Y_mном) вектора Y. В очередном (i + 1)-м варианте среди оставшихся n вариантов задается отклонение ... x_i от номинального значения только по одному из варьируемых параметров. В результате выполнения (i + +1)-го варианта получают для вектора Y значение Y_i = (y_1i, y_2i, ..., y_mi), по которому оценивается очередной i-й столбец матрицы абсолютной чувствительности A_i = (Y_i - Y_ном)/...x_i. Любой из найденных коэффициентов a_ji легко пересчитать в коэффициент b_ji в соответствии с данными работы.

Основное достоинство метода приращений - его универсальность: метод применим к любым непрерывным математическим моделям.

Однако у метода приращений имеются и существенные недостатки: невысокая точность, что характерно для операций численного дифференцирования; сравнительно большая трудоемкость вычислений. Трудоемкость вычислений оценивается количеством обращений к модели, так как объем вычислений в алгоритмических моделях обычно велик и заметно превышает трудоемкость выполнения процедур по обработке результатов обращений к моделям. В методе приращений требуется n + 1 вариант обращения к модели.

Прямой и вариационный методы. Эти методы анализа чувствительности менее универсальны, чем метод приращений, но позволяют повысить точность или снизить затраты машинного времени. Они основаны на интегрировании специальных систем обыкновенных дифференциальных уравнений, относятся к специальному ма тематическому обеспечению и применяются в подсистеме схемотехнического проектирования.

Регрессионный метод. В регрессионном методе анализа чувствительности коэффициенты чувствительности отождествляются с коэффициентами регрессии, рассчитываемыми в процессе статистического анализа по методу Монте-Карло. Этот метод требует выполнения очень большого объема вычислений; его применение выгодно, если в каком-либо маршруте проектирования нужно решать задачи как статистического анализа, так и анализа чувствительности. Тогда затраты времени, дополнительные к затратам на статистический анализ, будут пренебрежимо малы.

Статистический анализ

Цель статистического анализа - получение оценок рассеяния выходных параметров Y и вероятностей выполнения заданных условий работоспособности для проектируемого объекта. В случае объектов типа систем массового обслуживания сами выходные параметры имеют вероятностный смысл, тогда цель статистического анализа - расчет таких параметров. Причинами рассеяния выходных параметров Y являются нестабильность внешних параметров Q и случайный характер внутренних параметров Х. Результатами статистического анализа могут быть гистограммы выходных параметров, оценки математических ожиданий M_j и среднеквадратичных отклонений ... y_j каждого из выходных параметров ..y_j от номинальных значений, оценки коэффициентов корреляции r_ji между параметрами y_j и x_i, а также выходные параметры систем массового обслуживания. В качестве исходных данных фигурируют статистические сведения о рассеянии внутренних параметров и данные ТЗ о допустимых диапазонах изменения или законах распределения внешних параметров.

Статистический анализ исключительно важен, поскольку его результаты позволяют прогнозировать процент выхода годных изделий при их серийном изготовлении, т.е. оценить серийнопригодность проектируемого объекта. Если в исходных данных отразить старение внутренних параметров - их изменение в процессе эксплуатации и хранения под действием различных физико-химических факторов, то результаты статистического анализа можно непосредственно использовать для оценки надежности.

Наибольшее распространение в САПР при статистическом анализе получили методы наихудшего случая и статистических испытаний.

Метод наихудшего случая. Этот метод служит для определения диапазонов возможного рассеяния выходных параметров без оценки плотности распределения этих параметров.

Пусть на некоторый выходной параметр у задано условие работоспособности в виде у < тт. Тогда интерес представляет верхняя граница диапазона рассеяния, так как большие значения у наиболее опасны с точки зрения невыполнения условия работоспособности. Верхняя граница диапазона рассеяния достигается в наихудшем случае, когда все аргументы функциональной зависимости y = f(X) принимают самые неблагоприятные значения. Самым неблагоприятным значением аргумента X_i будет максимально возможное значение X_imax = x_iном + x_i при выполнении условий у < тт и dy/dx_i> 0 или у > тт и dy/dx_i< 0. Самым неблагоприятным значением аргумента X_i будет минимальное значение X_imin = x_iном - x_i, если (Y < тт 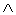dy/dx_i< 0) V (Y > тт 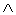dy/dx_i> 0). Здесь x_i - допуск на внутренний параметр X_i. При этом предполагается, что знаки коэффициентов влияния остаются неизменными в пределах рассматриваемой области.

Алгоритм метода наихудшего случая включает в себя следующие операторы:

1. Анализ чувствительности, в результате которого определяются коэффициенты чувствительности dy/dx_i.

2. Задание параметрам X_i самых неблагоприятных значений.

3. Расчет выходных значений параметров при неблагоприятных внутренних.

Выполнение анализа объекта в наихудшем случае. Каждому выходному параметру соответствует свой наихудший случай. Если объект характеризуется m выходными и n внутренними параметрами, то операторы 2 и 3 алгоритма повторяются m раз и всего требуется выполнить m + n + 1 вариантов обращения к модели объекта. Преимущество метода наихудшего случая в том, что для его применения не требуется знания законов распределения внутренних параметров. Достаточно знать лишь допуски x_i. Недостаток метода в том, что результаты анализа в наихудшем случае могут ввести в заблуждение пользователя относительно реального рассеяния выходных параметров.

Метод Монте-Карло (метод статистических испытаний). Этот метод позволяет получить более полные статистические сведения о выходных параметрах исследуемого объекта. Алгоритм метода статистических испытаний включает в себя следующие основные операторы:

1. Задание значений внутренних и внешних параметров (аргументов зависимости Y от Х и Q в очередном статистическом испытании).

2. Расчет Y.

3. Накопление статистических сумм.

4. Обработка накопленных сумм для получения результатов статистического анализа.

Операторы 1-3 выполняются в каждом испытании и могут быть распараллелены. Оператор 4 завершает статистический анализ. Задание значений случайных параметров выполняется в соответствии с их законами распределения. Подпрограммы выработки псевдослучайных чисел для величин, распределенных по таким законам, как нормальный, равномерный, экспоненциальный, имеются в составе общего программного обеспечения большинства ЭВМ. Однако в практике проектирования могут встретиться задачи с коррелированными исходными данными, имеющими любое распределение. Часто исходные данные получают как результаты измерений параметров на партии изделий и представляют в виде гистограмм. Тогда алгоритм задания случайных значений параметров целесообразно построить на основе следующего преобразования: X = 0(AZ), где 0 - оператор преобразования значений нормально распределенных величин в значения внутренних параметров, имеющих заданные распределения; Z - реализация n-мерного некоррелированного случайного вектора, элементы которого имеют нормированное нормальное распределение, т.е. характеризуются нулевыми математическими ожиданиями и единичными дисперсиями; Х - реализация n-мерного случайного вектора внутренних параметров в очередном статистическом испытании; А - матрица преобразования вектора Z в нормальный вектор с коррелированными элементами.