Однопериодная биномиальная модель

Пусть в текущий момент времени 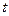цена актива равна . Предположим, что в момент времени возможны только два исхода: цена актива равна:

при

или

при

S(t), c

Вычислим текущую цену с опциона колл на этот актив со временем исполнения и ценой исполнения .

Опцион будет реализован, если рыночная цена актива окажется выше, чем цена исполнения.

Следовательно, цена опциона в момент исполнения:

Возможные значения цены опциона обозначаются и . Они равны:

или

Сформируем безрисковый портфель в момент времени 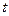, состоящий из одной акции и опционов колл.

Число подбирается так, чтобы цена портфеля в момент была одинаковой при любом из двух возможных значений . В этом случае портфель будет безрисковым и в момент времени .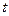

Если цена актива , то цена портфеля в момент времени равна

Если цена актива , то цена портфеля в момент времени равна

Приравнивая эти цены, получим уравнение для .

Значит,

Легко сообразить, что полученное число отрицательное. Это означает, что опционов, входящих в безрисковый портфель, нужно продавать.

Цена безрискового портфеля в момент времени равна

Согласно формуле (3.1), цена этого портфеля в момент времени 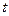вычисляется по формуле (предполагается постоянный процент – коэффициент дисконтирования)

Естественно считать, что ожидаемая прибыль от актива пропорциональна цене актива и времени работы актива .

Если неопределенность рыночной цены отсутствует, и коэффициент пропорциональности прибыли от цены актива и времени равен , то цена актива (при условии, что достаточно мало, так что коэффициент пропорциональности не изменяется) удовлетворяет уравнению:

(2.1)

или

При уравнение (2.1) становится дифференциальным

Его решение определяет цену актива в момент времени .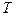

С другой стороны, цена портфеля равна

где - текущая цена опциона

Из двух равенств

и

следует:

или

, (3.8)

где

Напомним, что

и

Аналогично, цена опциона пут вычисляется по формуле:

, где

, .

Двухпериодная биномиальная модель

S(t), c

Вычисление цены опциона на актив с исполнением в конце второго периода по цене нужно начинать с конца.

Если в конце первого периода цена актива равна , то цену опциона можно вычислить в рамках однопериодной модели по формуле (3.8):

или для другого варианта цены, а именно :

Тогда цена опциона в начальный момент времени 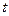выражается через и по формуле (3.8). Подставляя полученные выражения для и получим

,

где