С. Результаты комбинирования ценных бумаг

Ожидаемая доходность комбинации двух и более ценных бумаг

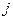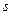Ожидаемая доходность комбинации ценных бумаг и с известными ожидаемыми доходностями:

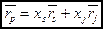, где

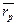- искомая средняя доходность портфеля;

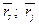- известные средние доходности каждой ценной бумаги;

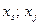- доли ценных бумаг двух видов в общем портфеле.

Если заметить, что

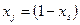,тогда

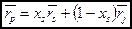
Формула доходности двух ценных бумаг может быть обобщена на портфель из 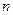различных ценных бумаг:

Риск инвестиционного портфеля

Если портфель состоит из двух ценных бумаг ( и 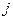), а весами являются их дол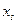и ( и 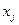) в портфеле, тогда из основного определения дисперсии (волатильности) пишем:

.

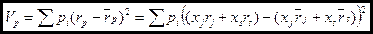Путем простых преобразований приходим к следующему (подробный вывод см. в Приложении к модели Г. Марковица):

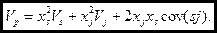
или

,

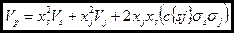где

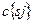- коэффициент корреляции доходностей двух ценных бумаг

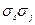- среднеквадратические отклонения распределения доходностей двух ценных бумаг

Если учесть, что дисперсия есть частный случай ковариации случайной величины с самой собой, то выведенная формула может быть распространена на измерение риска портфеля из любого количества ценных бумаг:

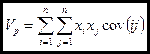
Напомним формулы коэффициента корреляция и ковариации между доходностями двух ценных бумаг, которые выведены в представленной работе вместе с выведением формулы дисперсии для суммы дисперсий случайных величин:

Коэффициент корреляции:

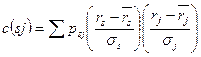, где

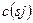- коэффициент корреляции между двумя акциями

Коэффициент ковариации

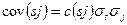
В связи с этими расчетами Бромвич М. еще раз отмечает, что теория инвестиционного портфеля не предполагает, что средний инвестор действительно будет осуществлять такие сложные расчеты, необходимые для получения коэффициента корреляции для каждой пары ценных бумаг из всего множества, которые ему, возможно, приходится рассматривать. Скорее, она предполагает, что инвестор может каким-то способом прийти к заключению относительно связи между доходностями от двух различных ценных бумаг.

D. Графическое определение взаимосвязи риска и доходности для инвестиционного портфеля, состоящего из ценных бумаг двух видов

Доходность портфеля

Ожидаемая доходность комбинации ценных бумаг и 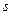с известными ожидаемыми доходностями:

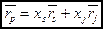
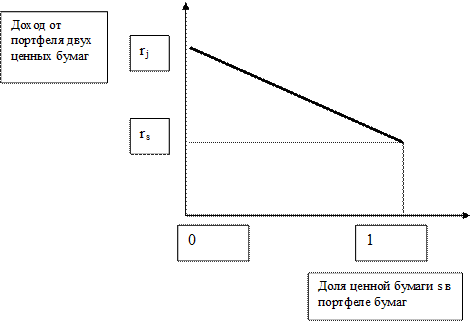
Рис. 4. Связь рентабельности и структуры портфеля

Риск портфеля

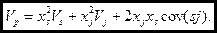
или

,

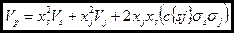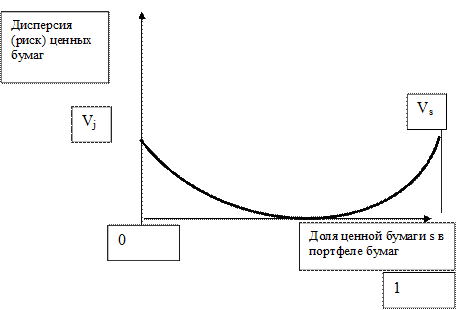
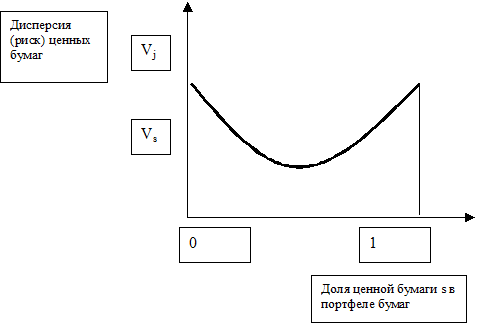
Очевидно, что риск портфеля при разумном сочетании ценных бумаг может быть ниже уровня неопределенности, связанной с каждой отдельной бумагой. Величина снижения риска зависит от степени корреляции между ценными бумагами

Рассмотрим возможные варианты графика дисперсии (волатильности) портфеля при упрощающих предположениях

Напомним, что риск портфеля ценных бумаг двух видов определяется так

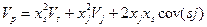
или

,

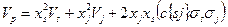где

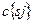- коэффициент корреляции двух ценных бумаг

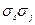- квадратические отклонения в распределении двух ценных бумаг

Учитывая, что 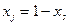, можно написать:

.

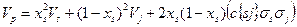Учитывая, что первые два слагаемые правой части положительны, а коэффициент корреляции изменяется от (+1) до (- 1), дисперсия портфеля должна уменьшаться при движении коэффициента корреляции от (+1) до (- 1).

А) Если коэффициент корреляции равен 1, то есть, в случае линейной положительной корреляции двух ценных бумаг, выражение для дисперсии портфеля примет вид:

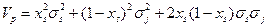
Или

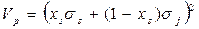
В этом случае дисперсия портфеля, а значит, риск, становятся максимальными.

Если предположить для простоты, что дисперсии двух ценных бумаг одинаковы, или:

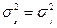, то риск портфеля максимален и представляется прямой горизонтальной линией

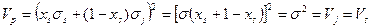
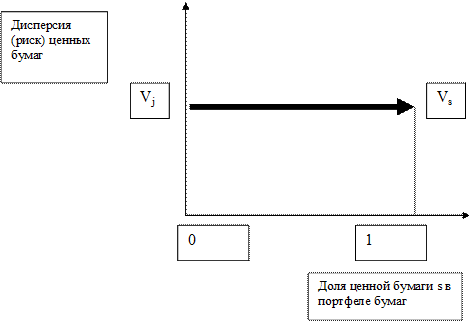
Рис. 5. Связь риска (дисперсии) и структуры для портфеля с одинаковыми дисперсиями двух ценных бумаг и коэффициентом корреляции (+1)

Б) Если корреляция между двумя ценными бумагами уменьшается до 0, дисперсия становится следующей:

.

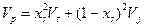пр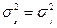и или 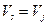имеем:

.

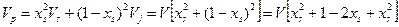Найдем точку оптимума, приравняв производную по 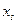к нулю.

.

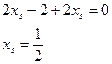Очевидно, что при 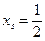, риск достигает минимума (половины риска каждой ценной бумаги)

.

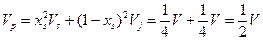Рис. 6. Связь риска (дисперсии) и структуры для портфеля с одинаковыми дисперсиями двух ценных бумаг и коэффициентом корреляции 0

В) Дисперсия (риск) минимальны, когда корреляция двух ценных бумаг равна (-1):

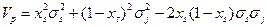
или

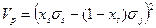
Опять же, если обратиться к нашему упрощающему предположению о равенстве дисперсий двух бумаг

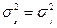или 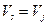имеем при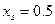

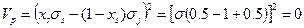
Рис. 7. Связь риска (дисперсии) и структуры для портфеля с одинаковыми дисперсиями двух ценных бумаг и коэффициентом корреляции (-1)