Решение задачи поиска экстремума функции градиентным методом. Поиск условного экстремума функции. Решение задач линейного программирования

(4часа)

Цель:сформировать у студентов умение решать задачи поиска экстремума функции одной и нескольких переменных.

Задания:

1. Найти максимальное и минимальное значение функции графическим методом.

2. Найти максимальное и минимальное значение функции, используя Excel, MathCad.

В таблице 4 приведены варианты задания 1. В таблице 5 приведены варианты задания 2.

Таблица 4 - Варианты задания 1

№ Вар.	Задание	№ Вар.	Задание

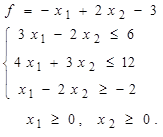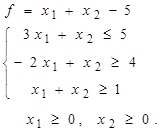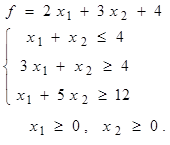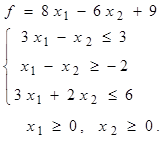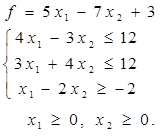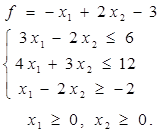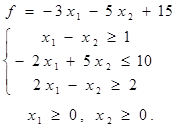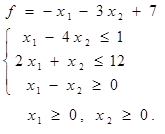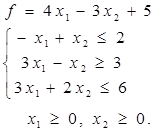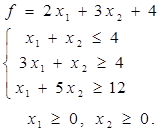Окончание таблицы 4

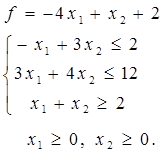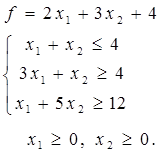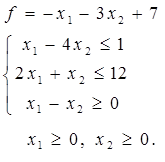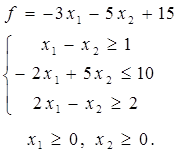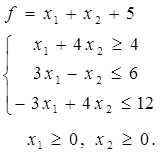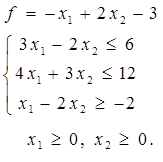В таблице 5 приведены варианты задания 2.

Таблица 5 - Варианты задания 2

№ Вар.	Задание	№ Вар.	Задание

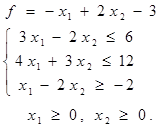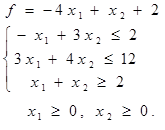Окончание таблицы 5

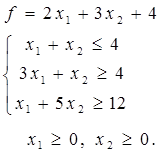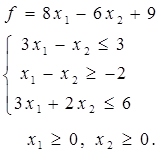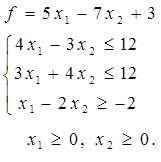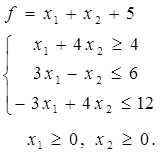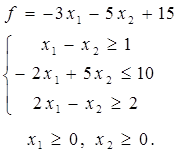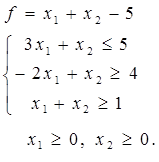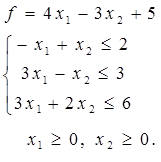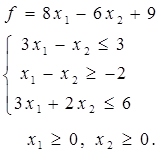Порядок выполнения лабораторной работы.

Для выполнения задания 1 необходимо:

1. Построить область допустимых решений (ОДР), заданную системой неравенств.

2. Построить вектор-градиент и линию уровня функции .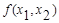

3. Определить точки входа и выхода в ОДР.

4. Указать максимальное и минимальное значение функции в построенной области.

Для выполнения задания 2 необходимо:

1. Найти максимальное и минимальное значение функции при указанных условиях, используя возможности Excel, MathCad.

Контрольные вопросы.

2. Сформулируйте необходимые условия существования экстремума функции двух переменных.

3. Сформулируйте достаточные условия существования экстремума функции двух переменных.

4. Что показывает градиентом функции?

5. Изложите суть градиентных методов поиска экстремума функции.

6. Сформулируйте постановку оптимизационной задачи.

7. Что называется условным экстремумом функции? Как находится условный экстремум функции?

8. Как найти локальный экстремум функции?

9. Как решить оптимизационные задачи, применяя современные вычислительные системы?

Лабораторная работа №4

Поиск экстремумов в инженерно-технических задачах

(2 часа)

Цель: сформировать у студентов умение находить экстремум в инженерно-технических задачах

Задания: Решить задачу поиска экстремума согласно своему варианту.

Задачи

Задача 1. Из железного листа длиной 4,3 м и шириной 2,3 м. отгибом полосок со всех четырех сторон изготовить: а) ящик объемом V₀ =1,2 м³; б) ящик максимального объем. Найти соответствующие размеры ящиков.

Задача 2. Сила тока в цепи определяется по закону Ома по формуле 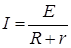, где R – внешнее сопротивление, r – внутреннее сопротивление. Мощность выражается формулой 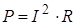. Найти значение R, при котором мощность будет наибольшей.

Задача 3.При каких линейных размерах закрытый цилиндрический резервуар данной вместимости V будет иметь наименьшую площадь полной поверхности?

Задача 4.Из круглого бревна диаметромd вырезать балку прямоугольного сечения так, чтобы площадь этого сечения была наибольшей. Указать размеры балки

Задача 5.Канал, подводящий воду к турбине, имеет в сечении форму равнобедренной трапеции. Ширина верхней части канала равна b. Угол откоса равен a. Найти глубину канала, при которой канал будет пропускать наибольшее количество воды.

Задача 6.Из железного листа длиной 4.1 м и шириной 2.1 м. отгибом полосок со всех четырех сторон сделать: а) ящик объемом V₀ =1м³; б) ящик максимального объем. Найти соответствующие размеры ящиков.

Задача 7.Канал, подводящий воду к турбине, имеет в сечении форму прямоугольника, ограниченного сверху полукругом. Периметр сечения равен Р. Найти размеры сечения канала.

Задача 8.Найти высоту конической воронки наибольшего объема, если ее образующая равна l.

Задача 9.Требуется построить открытый цилиндрический резервуар вместимостью 300 м³ воды. Стоимость материала, из которого делается дно резервуара, в два раза больше стоимости материала, идущего на боковые стенки. При каких размерах резервуара постройка его будет наиболее дешевой?

Задача 10.Определить размеры открытого бассейна объемом 32 м³ так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.

Задача 11.Из круглого бревна, диаметр которого равен 60 см, требуется вырезать балку прямоугольного сечения наибольшей жесткости. Жесткость равномерно нагруженной балки прямоугольного сечения пропорциональна величине ah³, где а – основание прямоугольного сечения, h – его высота (наибольшая жесткость равна наименьшей величине прогиба балки). Указать размеры балки.

Задача 12.Из круглого бревна, диаметр которого равен d, требуется вырезать балку прямоугольного сечения. Каковы должны быть размеры этого сечения, чтобы балка оказывала наибольшее сопротивление на изгиб. Сопротивление на изгиб пропорционально произведению ширины поперечного сечения на квадрат его высоты.

Задача 13.Требуется вырыть ров с поперечным сечением в виде равнобочной трапеции, у которой основание и боковые стороны равны а см. Каким должен быть угол откоса, чтобы вместимость рва оказалась наибольшей.

Задача 14.Зависимость полезной мощности от тока нагрузки выражается формулой 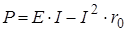. Определить величину тока нагрузки, при которой полезная мощность будет максимальной.

Задача 15.Прямоугольный участок земли площадью 600 м³ требуется огородить забором и разделить на три равные части перегородками, построенными параллельно одной из сторон прямоугольника. Каковы должны быть размеры участка, чтобы на постройку забора и перегородок пошло наименьшее количество материала. Найти, сколько материала потребуется.

Контрольные вопросы

1. Сформулируйте необходимое условие существования экстремума функции одной переменной. Почему это условие не является достаточным?

2. Сформулируйте достаточные условия существования экстремума функции одной переменной.

3. Как найти локальный экстремум функции?

4. В чем состоит графический метод поиска наибольшего и наименьшего значений функции в замкнутой ограниченной области?

5. Как решить оптимизационные задачи, применяя современные вычислительные системы?