Видоизмененный (упрощенный) метод Ньютона

Если производная на отрезке изменяется мало, то в формуле можно положить

Отсюда для корня 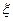уравнения получаем последовательные приближения . (14.14)

Геометрически этот способ означает, что мы заменяем касательные в точках прямыми, параллельными касательной к кривой в ее фиксированной точке

Формула (14.14) избавляет от необходимости каждый раз вычислять значения производной . Она очень полезна, когда функция 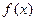сложна и трудно дифференцируется.

Комбинированный метод (хорд и касательных).

Пусть сохраняют постоянные знаки на отрезке . Объединяя способ пропорциональных частей (метод хорд) и метод Ньютона (метод касательных), получаем метод, на каждом этапе которого находим значения по недостатку и значения по избытку точного корня 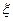уравнения .

Теоретически возможны четыре случая:

1). ;

2). ;

3). ;

4). .

Ограничимся рассмотрением 1-го случая. Остальные случаи изучаются аналогично.

Итак, пусть при . Полагаем ; ,

и (метод хорд),

(метод касательных). (14.15)

Очевидно, что , поэтому

. (14.16)

Если допустимая абсолютная погрешность приближенного корня задана заранее и равна , т.е. , то процесс сближения прекращается в тот момент, когда будет обнаружено, что . По окончании процесса за значение корня 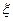лучше всего взять среднее арифметическое полученных последних значений: .

Пример. Вычислить с точностью до 0,0005 единственный положительный корень уравнения .

Решение. Из самого уравнения видно, что корни надо искать в окрестности точки . Находим, что . Поэтому .
Имеем: и Видим, что в выбранном нами интервале т.е. знаки производных сохраняются.

Применим комбинированный метод, полагая и

Вычисляем ; .

Подставляя эти значения в уравнения (14,15), получаем:

Оцениваем при :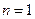

.

Видим, что точность пока недостаточная. Поэтому находим следующую пару приближений:

;

.

Опять оцениваем .

Нужная степень точности достигнута.

За значение искомого корня можно принять .

Абсолютная погрешность складывается из и

ошибки округления .

Метод итераций

(метод последовательных приближений)

Метод итераций является одним из наиболее важных способов численного решения уравнений. Сущность этого метода заключается в следующем. Пусть дано уравнение: (14.7)

где 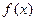-непрерывная функция, и требуется определить его вещественные корни. Заменим уравнение (14.7) равносильным уравнением

(14.8)

Выберем каким-либо способом грубо приближенное значение корня 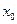и подставим его в правую часть уравнения (14.8). Получаем некоторое число

. (14.9)

Подставляя теперь в правую часть равенства (14.9) вмест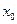о число 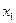, получим новое число .

Повторяя этот процесс, получаем последовательность чисел

. (14.10)

Если эта последовательность сходящаяся, т.е. существует предел , то, переходя к пределу в равенстве (14.10) и, предполагая функцию 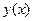непрерывной, найдем:

или . (14.11)

Таким образом, предел 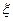является корнем уравнения (14.8) и может быть вычислен по формуле (14.10) с любой степенью точности.

Геометрически способ итерации может быть пояснен следующим образом. Построим на плоскости графики функций и Каждый действительный корень уравнения (14.8) является абсциссой точки пересечения М кривой с прямой (см. рис. 13.11).

Начиная с точки , строим ломаную линию ("лестницу"), звенья которой попеременно параллельны то оси , то оси . Вершины лежат на кривой , - на прямой . Общие абсциссы точек ,…, представляют собой последовательные приближения корня .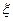

Возможен и другой вид ломаной - "спираль":

Нетрудно видеть, что решение в виде «лестницы» получается, когда производная положительна, а решение в виде «спирали», если отрицательна.

На приведенных рисунках кривые - пологие, т.е. , и процесс итерации сходится. Однако, если рассмотреть случай, где , то процесс итерации может быть расходящимся. Поэтому надо выяснить достаточные условия сходимости итерационного процесса.

Теорема. Последовательность сходится к корню x уравнения , если для любых и , принадлежащих , выполняется условие Липшица: . При этом нулевое приближение .

Доказательство.Так как x_n+1 = j (x_n) по условию итерации, а из того факта, что x - корень уравнения , очевидно равенство .

Но так как q< 1, то . Из этих неравенств и из условия при q < 1следует неравенство

,

где .

.

Следовательно, и , что и требовалось доказать.

Равносильной предыдущей является следующая

Теорема. Пусть функция определена и дифференцируема на отрезке . Тогда, если существует q такое, что

при a< x < b, то: 1) процесс итерации

сходится независимо от начального значения ;

2) предельное значение является единственным корнем уравнения на отрезке [a, b].

Первая часть последней теоремы доказывается аналогично предыдущей. Пункт 2) очевиден из рисунка. Для того чтобы график функции в окрестности значения x = x еще раз пересекся с графиком y₁ = x (условие наличия второго корня), он обязательно должен иметь на некоторых участках такое направление, которое требует выполнение условия . А это противоречит условию теоремы. Следовательно, второго корня уравнения на [a, b] не существует.

Замечание 1. Теорема остается верной, если функция j(x) определена и дифференцируема в бесконечном интервале -¥ < x < +¥, причем при x Î (-¥, +¥) выполнено неравенство .

Замечание 2. В условиях теоремы процесс итерации сходится при любом выборе начального значения x₀ из [a, b]. Благодаря этому он является «самоисправляющимся», то есть отдельная ошибка в вычислениях, не выводящая за пределы отрезка [a, b], не повлияет на конечный результат, так как ошибочное значение можно рассматривать как новое начальное значение x₀. Может возрасти лишь объем работы. Это свойство самоисправленияделает метод итерации одним из надежнейших методов вычислений.