Для удобства в вычислениях вместо дробных индексов вводят целочисленные, т.е

.

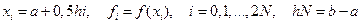И формула Симпсона принимает вид

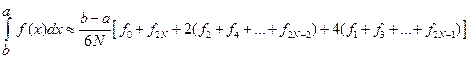(13.15)

Заметим, что формула (13.15) является точной для любого многочлена третьей степени т.е. имеет место точное равенство

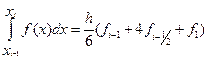, если .

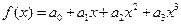Проверим эту формулу для приведенной функции на закрытом интервале .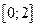

Непосредственное интегрирование дает:

.

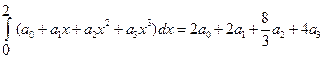Найдем этот интеграл с помощью формулы (13.15).

Здесь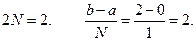

.

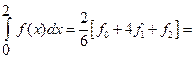
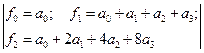
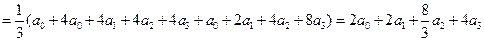Оценки погрешности для формулы Симпсона дают следующее выражение

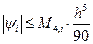. (13.16)

На всем отрезке :

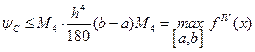(13.17)

Формула Ньютона (правило трех восьмых):

Еще одной формулой численного интегрирования является следующая, которая называется формулой Ньютона:

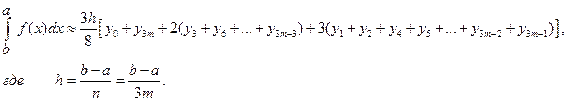
Остаточный член имеет вид

.

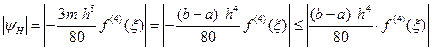В последней формуле число узлов обязательно равно .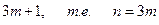

Если функция задана таблично и ее производные найти трудно, то в предположении отсутствия быстро колеблющихся составляющих можно применять приближенные формулы для погрешностей, выраженных через конечные разности:

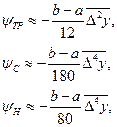
где под 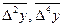подразумеваются арифметические средние значения разностей соответствующего порядка.

Использование сплайнов.

Одним из эффективных методов численного интегрирования является метод сплайнов, использующий интерполяцию сплайнами.

Разобьем отрезок интегрирования на частей точками .

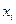Пусть 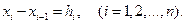На каждом элементарном участке функцию

интерполируем с помощью кубического сплайна

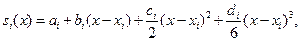(13.18)

.

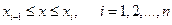Выражение для интеграла представим в виде

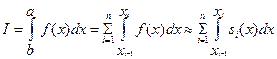(13.19)

Используя (13.18), вычисляем интеграл (13.19)

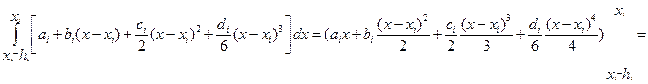
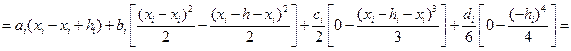
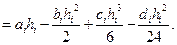
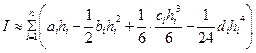. (13.20)

Способ нахождения коэффициентов 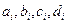был описан выше (см. "приближение сплайнами").

Порядок оценки погрешности приближения сплайнами приводился выше: 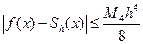(для кубического сплайна, построенного на сетке

, ).

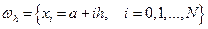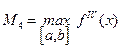Погрешность интегрирования с использованием сплайнов на отрезке 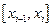может быть оценена из 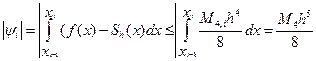, (13.21)

.

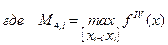Суммарная погрешность интегрирования на всем отрезке складывается из погрешностей интегрирования на каждом из элементарных участков, т.е.

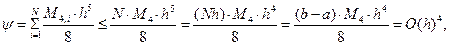
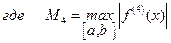. (13.22)

Другие методы.

Формулы Ньютона Котеса. Они получаются путем замены подынтегральной функции интерполяционным многочленом Лагранжа с разбиением отрезка на равных частей. Получающиеся формулы используют значения подынтегральной функции в узлах интерполяции и являются точными для всех многочленов некоторой степени, зависящей от числа узлов. Точность формул растет с увеличением степени интерполяционного многочлена. Кстати, формулы прямоугольников, трапеций и Симпсона являются частными случаями формул Ньютона – Котеса.

Метод Гаусса. Он не предполагает разбиения отрезка интегрирования на равные промежутки. Формулы численного интегрирования интерполяционного типа ищутся такими, чтобы они обладали наивысшим порядком точности при заданном числе узлов. Узлы и коэффициенты формул численного интегрирования ищутся из условий обращения в нуль их остаточных членов для всех многочленов максимально высокой степени (равносильно из условий минимизации остаточных членов при постоянстве количества узлов и степени многочлена).

Формула Эрмитаявляется частным случаем формул Гаусса. Использует многочлены Чебышева для определения узлов. Вычисляются интегралы вида

.

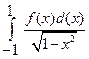Метод Маркова. Связан с формулами Гаусса. При выводе формул вводятся дополнительные предположения о совпадении точек разбиения отрезка по крайней мере с одним из его концов. (Вспомним, что полиномы Чебышева не дают узлов на концах отрезка интерполирования).

Формула Чебышева представляет интеграл в виде

.

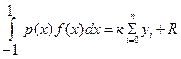При этом решается следующая задача: найти точки 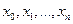и коэффициент такие, при которых остаточный член 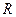обращается в нуль, когда функция является произвольным многочленом возможно большей степени.

Формула Эйлера использует не только значения подынтегральной функции в точках разбиения, но и ее производные до некоторого порядка на границах отрезка.