Вычисление квадратного корня

В качестве одного из многочисленных примеров рассмотрим нахождение точного значения квадратного корня.

Пусть .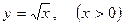

Положим .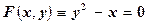

Тогда .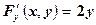

Применяя формулу (5.23),

,

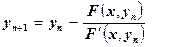имеем

,

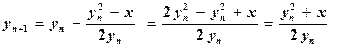или

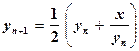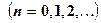, , (5.25)

(процесс Герона).

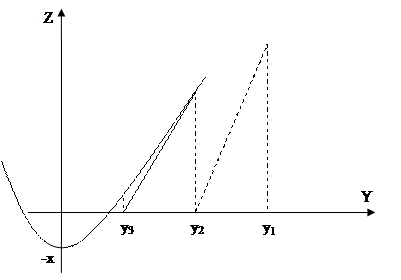
Рис.5.3. К вычислению квадратного корня.

Последовательные приближения 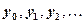получаются по методу Ньютона, примененному к параболе 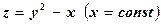. Если за у₀ принять табличное значение, дающее 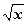с относительной погрешностью 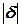, то у₁, определенное по формуле (5.25), дает новое значение 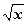приблизительно с относительной погрешностью .

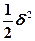Действительно, полагая

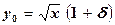
и пренебрегая степенями d, выше третьей, будем иметь:

.

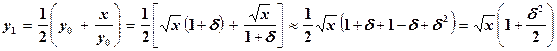Отсюда получаем вывод: при применении процесса Герона число верных цифр примерно удваивается на каждом этапе по сравнению с первоначальным количеством.

Пример 1. Для 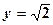приближенно имеем:

.

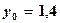Уточняя это значение, получаем

.

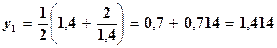Еще раз повторяя процесс, будем иметь:

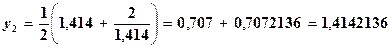, причем восемь или семь десятичных знаков являются верными. Действительно,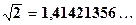

Приближение функций

При решении задач постоянно встречается необходимость замены одной функции некоторой другой функцией .

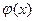Условнотакого рода задачи можно разделить на два типа:

1).Вид связи между параметрами и не известен, но эта связь задана в виде таблицы 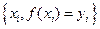, т.е. дискретному множеству значений аргумента 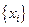поставлено в соответствие множество значений функции .

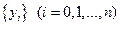Но при выполнении расчетов требуются и другие значения .

Эта цель достигается решением задачи о приближении (аппроксимации) функций: данную функцию требуется приближенно заменить (аппроксимировать) некоторой функцией 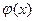так, чтобы отклонение 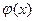от в заданной области было наименьшим. Функция 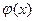при этом называется аппроксимирующей.

Для практики весьма важен случай аппроксимации ф-ций многочленами вида

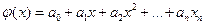(6.1)

В дальнейшем для аппроксимации будут рассматриваться лишь такие функции.

2). Вид связи 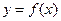известен. Например, 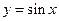. Очевидно, что при ручном счете могут быть использованы таблицы, где с определенной погрешностью приведены значения 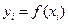. Но при машинном счете ввод таблиц требует больших затрат памяти. Поэтому для вычисления значений функций на ЭВМ используются разложения этих функций в степенные ряды. Например, функция 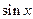вычисляется с помощью ряда

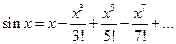(6.2).

Если приближение строится на заданном дискретном множестве точек 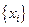, то аппроксимация называется точечной.

При построении приближения на непрерывном множестве точек аппроксимация называется непрерывной.

6.1 Точечная аппроксимация.

Одним из основных типов точечной аппроксимации является интерполирование. Оно состоит в следующем: для данной функции 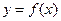строим многочлен (6.1), принимающий в заданных точках 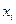те же значения 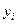, что и функция , т. е.

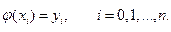(6.3)

При этом предполагается, что среди значений 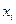нет одинаковых, т.е. x_i ≠ x_k при 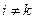. Точки 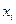называются узлами интерполяции, а многочлен 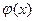-интерполяционным многочленом. Максимальная степень интерполяционного многочлена равна .

В этом случае мы имеем дело с глобальной интерполяцией, поскольку один многочлен

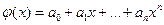
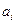используется для интерполяции функции на всем интервале изменения аргумента . Коэффициенты находятся из системы уравнений 6.3.

Если интерполяционные многочлены построить отдельно для разных частей рассматриваемого интервала изменения , то получим кусочную (или локальную) интерполяцию.

Если интерполяционные многочлены используются для приближенного вычисления функции вне рассматриваемого отрезка 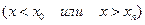, то такое приближение называют экстраполяцией.

Кроме интерполирования, где требуется выполнение условий 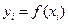возможны и другие виды аппроксимации. Например, в случае глобальной интерполяции при большом количестве узлов интерполяции получается высокая степень многочлена (6.1). В этом случае можно пойти другим путем: выбирается многочлен меньшей степени, график которого проходит близко от данных точек (штриховая линия на рис.6.1).

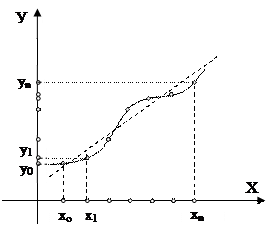Рис. 6.1. К вопросу об экстраполяции.

6.1.1. Одним из таких видов является среднеквадратичное приближение функций с помощью многочлена. При этом 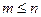; случай 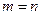соответствует интерполяции.

На практике стараются подобрать многочлен 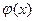как можно меньшей степени (как правило, .

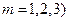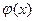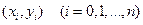Мерой отклонения многочлена от заданной функции на множестве точек при среднеквадратичном приближении является величина 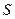, равная сумме квадратов разностей между значениями многочлена и функции в данных точках:

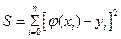(6.4)

Для построения аппроксимирующего многочлена нужно подобрать коэффициенты 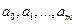так, чтобы величина 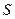была наименьшей. В этом состоит метод наименьших квадратов.