Составление эквивалентной операторной схемы
3. Расчет операторной схемы любым расчетным методом в операторной форме, преобразование изображения X(p) искомой величины к виду рациональной дроби.
4. Определение оригинала x(t) по X(p), т.е. обратный переход.
 |
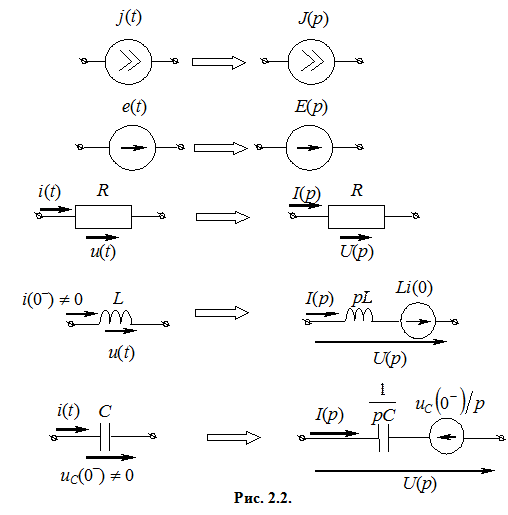Определение оригинала x(t) по изображению X(p)
Оригинал можно определить описанными ниже способами.
Использование обратного преобразования Лапласа
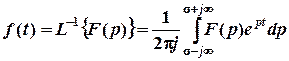, (2.1)
которое представляет собой решение интегрального уравнения относительно неизвестной функции f(t) и может быть получено методами теории функций комплексного переменного. Интеграл (2.1) вычисляется по прямой на плоскости комплексного переменного p, параллельной мнимой оси и расположенной правее всех особенностей (в частности, простых и кратных полюсов) функции F(p). Такой способ в прикладных задачах электротехники не используется.
Табличный метод. Подробные таблицы оригиналов и соответствующих им изображений приводятся в математических и электротехнических справочниках. При использовании этого способа возникают трудности, связанные с распознаванием и сведением функций к табличному виду.
Использование теоремы о вычетах или теоремы разложения.
Для каждой функции времени, входящей в уравнение Кирхгофа, описывающего расчетную цепь, устанавливается в соответствие операторное изображение, после чего система линейных дифференциальных уравнений переписывается в виде системы алгебраических уравнений (также получаем операторную схему замещения). Система алгебраических уравнений рассчитывается относительно операторного изображения искомой величины, по которому с помощью теоремы разложения находится оригинал.
Теорема разложения имеет две модификации в зависимости от вида операторного изображения искомой величины:
1) 
·=· 
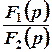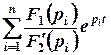, (2.2)
где n – порядок цепи,
pi – простые корни характеристического уравнения N(p) = 0;
.
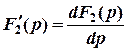2) 
·=· 
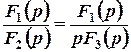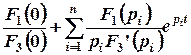, (2.3)
где pi – корни характеристического уравнения F3(p) = 0.
В этом случае знаменатель имеет один нулевой корень, на это указывает наличие в составе знаменателя множителя p. Теорема разложения в форме (2.3) соответствует сигналам, имеющим принужденную составляющую.
Если уравнение второго порядка, соответствующее цепи второго порядка, F2(p) = 0 имеет комплексные сопряженные корни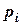 
и 
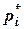, то достаточно вычислить слагаемое сумм (2.2) или (2.3) только для корня 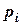, а для сопряженного корня 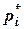взять значение, сопряженное этому слагаемому. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней:
·=· 
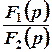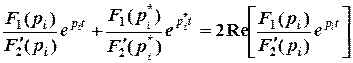(2.4)
Или
·=· 
.
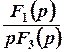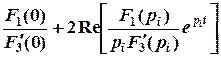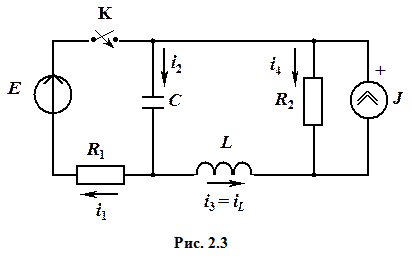
3. Пример расчета переходного процесса
В цепи II порядка
Дана цепь (рис. 2.3) с параметрами Е = 30 В , J = 2 А , R1 = 20 Ом , R2 = 10 Ом, С = 100 мкФ , L = 50 мГн .
Определить закон изменения тока i1(t) после коммутации.
