Задачи, приводящие к понятию определенного интеграла
Определенные интегралы, как и неопределенные интегралы, введены в математику Ньютоном и Лейбницем. К понятию неопределенного интеграла их привела проблема нахождения первообразных для заданной функции, то есть задача, обратная задаче нахождения производных функций. А к понятию определенного интеграла их привела совсем другая проблема - проблема точного решения ряда фундаментальных для практики числовых задач, к рассмотрению которых мы сейчас и переходим.
1.Задача о вычислении площади произвольной криволинейной трапеции.
 Рассмотрим рис. 1(а), где
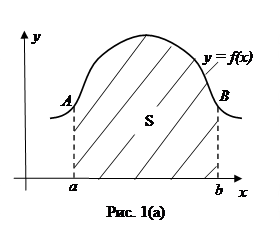
Рассмотрим рис. 1(а), где 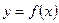 – некоторая непрерывная на
– некоторая непрерывная на 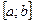 функция.
функция.
Заштрихованная на этом рисунке фигура называется криволинейной трапецией. А S - площадь этой трапеции. Поставим, вслед за Ньютоном и Лейбницем, задачу: вывести формулу для площади S этой трапеции при заданных a, b и f(x).
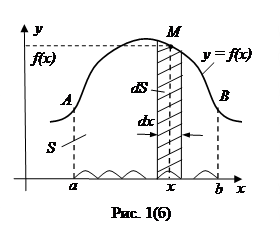
Решение. Разобьем мысленно отрезок 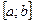 оси ох (основание трапеции) на бесконечно малые участки, как это показано на рис. 1(б). Для простоты будем считать их одинаковыми по длине. Эту бесконечно малую длину каждого участка обозначим символом dx. Если через концы этих участков провести вертикальные прямые, то вся криволинейная трапеция разобьется на бесконечно большое число бесконечно узких вертикальных полосок шириной dx. Рассмотрим одну из таких полосок (любую), и найдем ее площадь dS (см. рис. 1(б)).
оси ох (основание трапеции) на бесконечно малые участки, как это показано на рис. 1(б). Для простоты будем считать их одинаковыми по длине. Эту бесконечно малую длину каждого участка обозначим символом dx. Если через концы этих участков провести вертикальные прямые, то вся криволинейная трапеция разобьется на бесконечно большое число бесконечно узких вертикальных полосок шириной dx. Рассмотрим одну из таких полосок (любую), и найдем ее площадь dS (см. рис. 1(б)).
Возьмем в основании полоски некоторую произвольную точку х. Так как полоска бесконечно узкая (то есть она представляет собой вертикальную нить), то х – это точка, являющаяся основанием этой нити. Согласно рис. 1(б), площадь dS рассматриваемой полоски (нити) можно найти, умножив ее высоту f(x) на ширину dx. То есть
dS = f(x)dx (1)
Впрочем, такой была бы площадь dS полоски, если бы полоска была прямоугольником с основанием dx и высотой f(x). Но наша полоска имеет сверху криволинейную границу, а f(x) - высота, на которой находится лишь одна из точек (точка М) этой границы. Все остальные точки указанной верхней границы полоски находятся, вообще говоря, на другой, хоть и близкой к f(x), высоте. Так что формула (1) для площади каждой из полосок, на которые мы мысленно разбили криволинейную трапецию, не точная, а приближенная. Но очевидно, чем уже полоска, тем точнее формула для ее площади dS. А так как наша полоска (как и все остальные) не просто узкая, а бесконечно узкая, то мы вправе считать формулу (1) точной.
Складывая теперь площади dS всех вертикальных полосок, найдем, причем точно, и всю площадь S криволинейной трапеции:
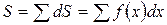 (2)
(2)
Эта сумма необычная: слагаемые в ней бесконечно малые, а число слагаемых бесконечно велико (S - суммабесконечно большого числа бесконечно малых слагаемых). Этой сумме Лейбниц дал специальное обозначение.
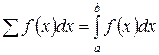 (3)
(3)
и назвал ее определенным интегралом от функции f(x). Здесь f(x)– подынтегральная функция; f(x)dx - подынтегральное выражение; x – переменная интегрирования; a и b - пределы интегрирования (нижний и верхний).
Итак, согласно (2) и (3),
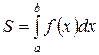 (4)
(4)
- площадь криволинейной трапеции, изображенной на рис. 1(а).
2. Задача о вычислении пути при переменной скорости движения.
Пусть некоторая материальная точка движения по некоторой траектории с известной в каждый момент времени 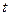 переменной скоростью
переменной скоростью 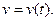 Требуется получить формулу для пути
Требуется получить формулу для пути 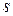 (перемещения), пройденного точкой по траектории своего движения с некоторого данного момента времени
(перемещения), пройденного точкой по траектории своего движения с некоторого данного момента времени 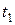 до некоторого данного момента времени
до некоторого данного момента времени 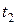 .
.
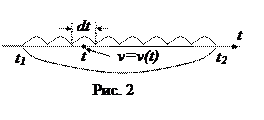 Решение. Если бы скорость
Решение. Если бы скорость 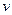 движения точки была постоянной, то поставленная задача никакого труда бы не представляла: путь равен скорости, умноженной на время. То есть
движения точки была постоянной, то поставленная задача никакого труда бы не представляла: путь равен скорости, умноженной на время. То есть 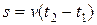 . Но у нас скорость точки
. Но у нас скорость точки 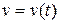 переменная (в разные моменты времени
переменная (в разные моменты времени 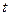 она разная). Для такого случая разобьем мысленно временной промежуток
она разная). Для такого случая разобьем мысленно временной промежуток 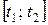 на бесконечно малые промежутки времени
на бесконечно малые промежутки времени 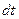 и найдем путь
и найдем путь 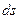 , проходимый точкой за каждое время
, проходимый точкой за каждое время 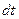 .
.
Рассмотрим один из промежутков 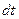 (любой) и выберем на этом промежутке некоторую точку (некоторый момент времени)
(любой) и выберем на этом промежутке некоторую точку (некоторый момент времени) 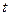 . В этот момент времени скорость движения точки равна
. В этот момент времени скорость движения точки равна 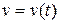 (рис.2). Практически такой же, в силу малости
(рис.2). Практически такой же, в силу малости 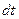 , она будет в других точках (в другие моменты времени) этого же промежутка времени. То есть можем считать, что в течение времени
, она будет в других точках (в другие моменты времени) этого же промежутка времени. То есть можем считать, что в течение времени 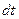 точка движется практически с постоянной скоростью
точка движется практически с постоянной скоростью 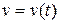 . А тогда путь
. А тогда путь 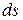 , пройденный точкой за время
, пройденный точкой за время 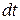 , найдется по формуле:
, найдется по формуле:
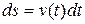 (5)
(5)
Впрочем, таким был бы путь 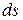 , если бы в течение времени
, если бы в течение времени 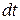 точка двигалась строго с постоянной скоростью
точка двигалась строго с постоянной скоростью 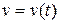 . Но эта скорость хоть и незначительно, но все же меняется в течение времени
. Но эта скорость хоть и незначительно, но все же меняется в течение времени 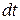 . Поэтому формула (5) не точная, а приближенная. Однако очевидно, что с уменьшением времени
. Поэтому формула (5) не точная, а приближенная. Однако очевидно, что с уменьшением времени 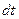 она будет становиться все точнее и точнее. А так как наш промежуток времени
она будет становиться все точнее и точнее. А так как наш промежуток времени 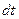 не просто мал, а бесконечно мал, то мы вправе считать формулу (5) точной.
не просто мал, а бесконечно мал, то мы вправе считать формулу (5) точной.
Складывая теперь пути 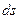 , пройденные точкой за все промежутки времени
, пройденные точкой за все промежутки времени 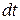 , найдем, причем точно, и общий путь
, найдем, причем точно, и общий путь 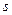 (общее перемещение точки по траектории ее движения) за время от момента
(общее перемещение точки по траектории ее движения) за время от момента 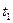 до момента
до момента 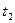 :
:
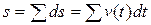 (6)
(6)
Формула (6) по своей структуре совершенно аналогична формуле (2). Она, как и формула (2), представляет собой сумму бесконечно большого числа бесконечно малых слагаемых. То есть представляет собой определенный интеграл вида (3):
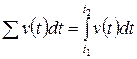 (7)
(7)
Итак, получаем окончательно: если 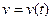 - переменная скорость движения точки, то перемещение
- переменная скорость движения точки, то перемещение 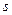 , пройденноеточкой по траектории ее движения, найдется по формуле:
, пройденноеточкой по траектории ее движения, найдется по формуле:
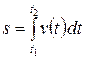 (8)
(8)
3.Задача о нахождении работы переменной силы
Пусть по оси ох из точки a в точку b под действием заданной переменной силы 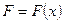 движется материальная точка (точка приложения силы
движется материальная точка (точка приложения силы 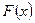 ) - см. рис. 3.
) - см. рис. 3. 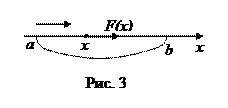 Требуется вывести формулу для работы А, которую совершит сила F(x) при перемещении материальной точки х из положения а в положение b.
Требуется вывести формулу для работы А, которую совершит сила F(x) при перемещении материальной точки х из положения а в положение b.
Решение. Если бы сила 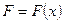 , приложенная к движущейся точке
, приложенная к движущейся точке 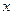 , была постоянной, то мы нашли бы работу
, была постоянной, то мы нашли бы работу 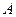 по известной школьной формуле
по известной школьной формуле 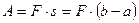 . Но у нас сила переменная - она меняется с изменением координаты
. Но у нас сила переменная - она меняется с изменением координаты 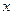 движущейся точки. В связи с этим разобьем мысленно промежуток [а; b] на бесконечно малые участки длиной
движущейся точки. В связи с этим разобьем мысленно промежуток [а; b] на бесконечно малые участки длиной 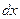 и найдем работу
и найдем работу 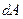 силы
силы 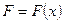 на каждом участке (рис. 4).
на каждом участке (рис. 4). 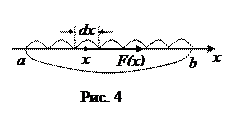
Если 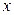 – некоторая точка на участке
– некоторая точка на участке 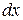 , то очевидно, что
, то очевидно, что
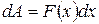 (9)
(9)
Мы записали эту формулу, считая, что в любой точке, находящейся на данном участке 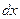 , сила, действующая на движущуюся точку, такая же, как и в выбранной точке
, сила, действующая на движущуюся точку, такая же, как и в выбранной точке 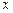 , то есть постоянная. Но это, вообще говоря, не так: во время прохода точкой участка
, то есть постоянная. Но это, вообще говоря, не так: во время прохода точкой участка 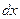 действующая на нее сила, хоть и незначительно, но меняется. Впрочем, изменение этой силы на
действующая на нее сила, хоть и незначительно, но меняется. Впрочем, изменение этой силы на 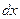 тем меньше, чем меньше
тем меньше, чем меньше 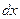 . А значит, с уменьшением
. А значит, с уменьшением 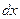 формула (9) будет становиться все точнее и точнее. Но так как наш участок
формула (9) будет становиться все точнее и точнее. Но так как наш участок 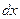 не просто мал, а бесконечно мал, то формулу (9) мы вправе считать точной.
не просто мал, а бесконечно мал, то формулу (9) мы вправе считать точной.
А теперь, складывая работы 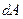 силы
силы 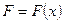 на всех участках
на всех участках 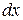 , на которые мы разбили отрезок [а; b], мы получим, причем точно, всю искомую работу А:
, на которые мы разбили отрезок [а; b], мы получим, причем точно, всю искомую работу А:
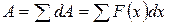 (10)
(10)
А так как, по аналогии с равенствами (2) и (7),
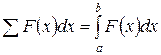 , (11)
, (11)
то получим окончательно:
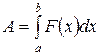 (12)
(12)
Это и есть формула для работы А, которую совершит переменная сила 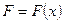 , если её точка приложения
, если её точка приложения 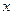 переместится вдоль оси ох из положения
переместится вдоль оси ох из положения 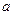 в положение
в положение 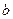 (рис. 3).
(рис. 3).
4.Задача о нахождении объема производства при заданной производительности труда
Пусть функция 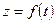 описывает изменение производительности труда рабочего, бригады или целого предприятия с течением времени
описывает изменение производительности труда рабочего, бригады или целого предприятия с течением времени 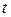 . Требуется найти формулу для объема
. Требуется найти формулу для объема 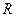 произведенной продукции с момента времени
произведенной продукции с момента времени 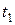
 до момента времени
до момента времени 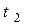 , где
, где 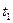 и
и 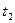 - заданные числа.
- заданные числа.
Решение. Если бы производительность труда 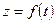 (количество продукции, производимой в единицу времени) была постоянной, то искомый объем
(количество продукции, производимой в единицу времени) была постоянной, то искомый объем 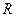 произведенной продукции мы нашли бы, умножив производительность труда на время работы, то есть нашли бы по формуле
произведенной продукции мы нашли бы, умножив производительность труда на время работы, то есть нашли бы по формуле 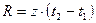 . Но, по условию, производительность труда
. Но, по условию, производительность труда 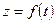 меняется со временем. Чтобы в этом случае найти искомый объем
меняется со временем. Чтобы в этом случае найти искомый объем 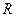 произведенной продукции, нужно, очевидно, разбить промежуток времени
произведенной продукции, нужно, очевидно, разбить промежуток времени 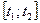 на бесконечно малые промежутки времени
на бесконечно малые промежутки времени 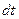 , выбрать внутри каждого
, выбрать внутри каждого 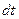 произвольную точку
произвольную точку 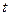 , найти объем
, найти объем 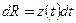 произведенной за время
произведенной за время 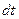 продукции, и сложить все
продукции, и сложить все 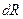 - то есть по существу проделать ту же процедуру, что была проделана в предыдущих трех задачах. В итоге получим формулу
- то есть по существу проделать ту же процедуру, что была проделана в предыдущих трех задачах. В итоге получим формулу
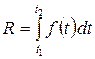 , (13)
, (13)
совершенно аналогичную формулам (4), (8) и (12). Эта формула выражает объем продукции, произведенной за время от 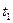 до
до 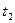 , через производительность труда
, через производительность труда 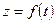 .
.
Итак, мы получим итоговые формулы (4), (8), (12) и (13) для четырех рассмотренных выше и имеющих важное практическое значение задач. Можно было бы и продолжить рассмотрение аналогичных задач, но мы ограничимся теми, что уже рассмотрели. Вместо этого осмыслим ту общую идею, которая была заложена при решении всех этих задач. А эта идея следующая: нужную нам величину мы мысленно разбиваем на бесконечно малые части, а затем, складывая все эти части (их бесконечно много!), получаем искомую величину. Эта величина оказывалась выраженной через новое математическое понятие - определенный интеграл. Теперь, очевидно, нужно понять, какими свойствами обладают определенные интегралы и как их вычислять.
Упражнения
1. Пусть отрезок [а; b] оси ox – материальная нить, у которой 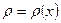 - заданная линейная плотность вещества, распределенного по этой нити (линейная плотность - это масса единицы длины). Получить формулу для массы
- заданная линейная плотность вещества, распределенного по этой нити (линейная плотность - это масса единицы длины). Получить формулу для массы 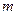 всей нити.
всей нити.
Ответ: 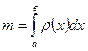 (14)
(14)
2. Пусть 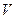 – объем тела вращения, образованного вращением криволинейной трапеции (рис.1(а)) вокруг оси ox . Получить формулу для объема
– объем тела вращения, образованного вращением криволинейной трапеции (рис.1(а)) вокруг оси ox . Получить формулу для объема 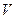 этого тела.
этого тела.
Ответ: 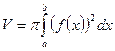 (15)
(15)
3. Пусть 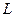 – длина участка
– длина участка 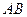 кривой
кривой 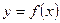 с абсциссами концов
с абсциссами концов 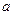 и
и 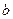 (рис. 5.1(а)). Получить формулу для длины этого участка.
(рис. 5.1(а)). Получить формулу для длины этого участка.
Ответ: 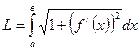 (16)
(16)
