Решение системы уравнений с помощью встроенных функций
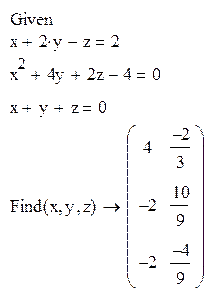
Рисунок 6 – Решение системы линейных уравнений
с помощью встроенных функций
Задание 2.1.Исследуйте систему линейных уравнений и, если решение существует, найдите его по формулам Крамера.
Вариант 1
1) 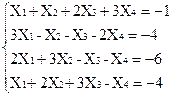 2)
2) 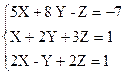
Вариант 2
1) 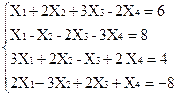 2)
2) 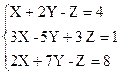
Вариант 3
1) 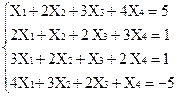 2)
2) 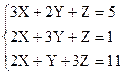
Вариант 4
1) 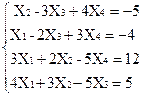 2)
2) 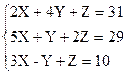
Вариант 5
1) 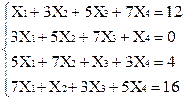 2)
2) 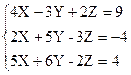
Вариант 6
1) 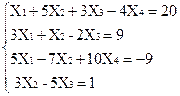 2)
2) 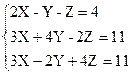
Вариант 7
1) 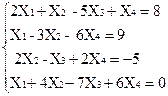 2)
2) 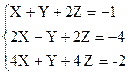
Вариант 8
1) 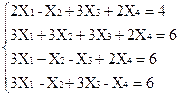 2)
2) 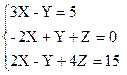
Вариант 9
1) 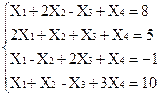 2)
2) 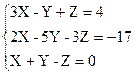
Вариант 10
1) 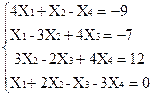 2)
2) 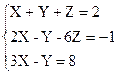
Вариант 11
1) 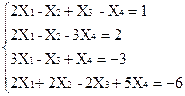 2)
2) 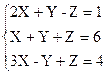
Вариант 12
1) 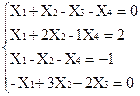 2)
2) 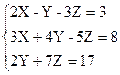
Порядок выполнения задания:
1. Установите режим автоматического выполнения вычислений.
2. Введите матрицу системы.
3. Вычислите определитель матрицы системы. Система имеет единственное решение, если определитель отличен от нуля.
4. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей.
5. Найдите решение системы по формулам Крамера.
Задание 2.2.Решить систему уравнений задания 2.1 с помощью обратной матрицы.
Порядок выполнения задания:
1. Введите матрицу системы и вектор-столбец правых частей.
2. Вычислите решение системы по формуле Х=А-1·В.
3. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
Задание 2.3.Решитьсистемулинейных уравнений задания 2.1 методом Гаусса.
Порядок выполнения задания:
1. Присвойте переменной ORIGIN значение, равное единице.
2. Введите матрицу системы и столбец правых частей.
3. Сформируйте расширенную матрицу системы.
4. Приведите расширенную матрицу системы к ступенчатому виду.
5. Сформируйте столбец решения системы.
6. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
Задание 2.4.Решить систему уравнений задания 2.1 с помощью встроенных функций Given и Find.
Порядок выполнения задания:
1. Записать служебное слово Given.
2. Ввести систему уравнений.
3. Вывести решение с помощью функции Find.
Практическая работа №3. Интерполирование функций
Задача интерполирования возникает в том случае, когда заданы результаты измерений yi = f(xi) некоторой величины f(x) в точках xi (i = 0, 1,…, n) и требуется определить ее значение в других точках, отличных от заданных. Интерполирование используется также, когда этих точек мало и такая зависимость оказывается не информативной и не наглядной. Такжекогда вычисление значений f(x) по точным формулам трудоемко, возникает необходимость приближенной замены (аппроксимации) данной функции (обычно заданной таблицей) другими функциями, которые легче вычислить. Задача заключается в подборе формулы, корректно описывающей экспериментальные данные.
