Интерполирование алгебраическими многочленами

Пусть функциональная зависимость задана таблицей y_{0 =} f(x₀);…, y₁= f(x₁);…,y_{n =} f(x_n). Обычно задача интерполирования формулируется так: найти многочлен P(x) = P_n(x) степени не выше n, значения которого в точках x_i (i = 0, 1 2,…, n) совпадают со значениями данной функции, то есть P(x_i) = y_i.

Геометрически это означает, что нужно найти кривую вида

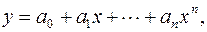
проходящую через заданную систему точек (x_i,y_i).

Многочлен Р(х) называется интерполяционным многочленом. Точки x_i (i = 0, 1, 2,…, n) называются узлами интерполяции.

Наиболее употребительна запись интерполяционного многочлена в форме Лагранжа и в форме Ньютона.

Интерполяционный многочленЛагранжаимеет вид:

.

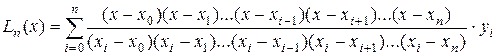или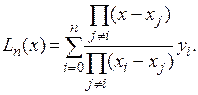

При n=1 получается формула линейной интерполяции, при n=2 – квадратичной интерполяции и т.д.

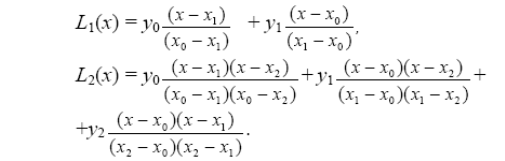
В системе MathCAD существуют встроенные функции линейной и сплайн-интерполяции. При линейной интерполяции узловые точки соединяются отрезками прямых. Если х выходит за пределы конечных точек, то осуществляется линейная экстраполяция по отрезкам прямых, примыкающим к конечным точкам. При сплайн-интерполяции зависимость у(х) заменяется кусками полиномов третьей степени. Каждый полином проходит точно через три ближайшие узловые точки. Коэффициенты полинома подбираются так, чтобы обеспечить не только непрерывность функции в узловых точках, но и непрерывность ее двух производных. Эти свойства сплайн-интерполяции позволяют эффективно применять ее даже при малом числе узловых точек – до 5-7 для простых функций.

Интерполяция реализуется с помощью следующих функций:

- linterp(X,Y,x) –вычисляет значение у(х) для заданного х при линейной интерполяции,

- cspline(X,Y) – вычисляет вектор V вторых производных при сплайн-интерполяции и кубической экстраполяции,

- pspline(X,Y) – вычисляет вектор V вторых производных при сплайн-интерполяции и параболической экстраполяции,

- lspline(X,Y) – вычисляет вектор V вторых производных при сплайн-интерполяции и линейной экстраполяции,

- interp(V,X,Y,x) – вычисляет значение у(х) для заданного х при сплайн-интерполяции.

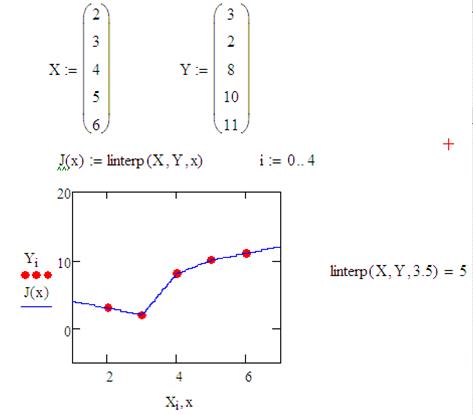
Рисунок 7 – Кусочно-линейная интерполяция

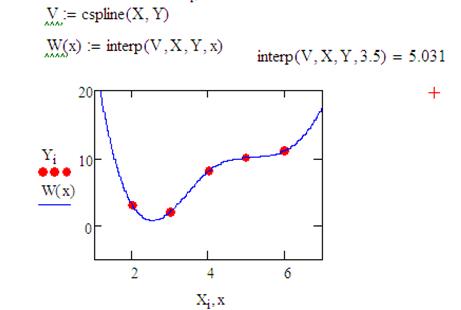
Рисунок 8 – Интерполяция сплайнами

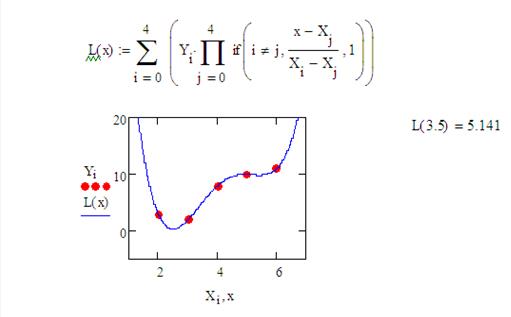
Рисунок 9 – Использование интерполяционного многочлена Лагранжа

Протабулируем функцию 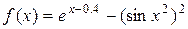на интервале [-1, 2] и вычислим одно значение заданной функции для промежуточного значения аргумента x=1 с помощью сплайн-интерполяции.

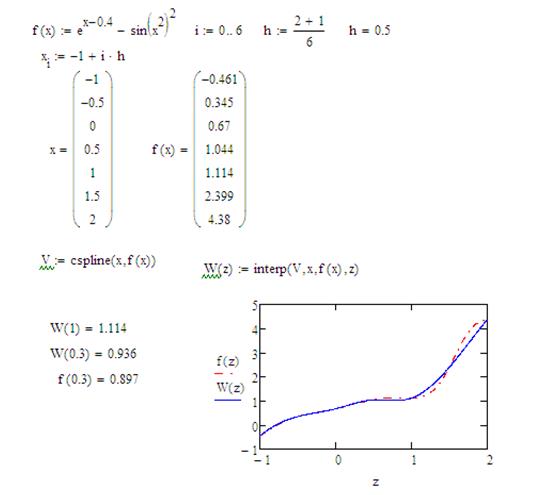
Рисунок 10 – Вычисление значения функции

с использованием сплайн-интерполяции

Задание 1.Определить значения функции в точках х1 и х2 в MathCAD, используя встроенные функции линейной, сплайн-интерполяции и многочлен Лагранжа. Построить графики исходной и интерполирующих функций.

Вариант 1

x	1,5		2,5		3,5
y	-11,844	-20	-23,281	-3,5	71,7813
x1=1,25	x2=2,75

Вариант 2

x	0,5		1,5		2,5
y	0,15625	-0,5	-1,7813		20,7813	82,5
x1=0,75	x2=2,25

Вариант 3

x	-2	-1
y	-101	-7,5		-3,5	-45	-183,5
x1=0,5		x2=2

Вариант 4

x
y		-10,5	-49	-37,5		1527,5
x1=0,5		x2=4,5

Вариант 5

x	0,5		1,5		2,5
y	5,0625		5,5625		19,0625
x1=0,75	x2=1,75

Вариант 6

x		1,5		2,5		3,5
y	-2	-2,5	0,5	11,125		79,25
x1=1,75	x2=2,75

Вариант 7

x	-1
y
x1=0,75	x2=2,25

Вариант 8

x	0,5		1,5		2,5
y	-2,1875	-2,25	-0,1875	7,75	26,8125	63,75
x1=1,7		x2=2,25

Вариант 9

x	-1
y	-3,5	-5,5	-5,5	2,5	48,5	186,5
x1=0,8		x2=2,5

Вариант 10

x	0,5		1,5		2,5
y	-0,8125	-1,75	-0,5625	6,5	24,6875	60,75
x1=0,75	x2=2,25

Вариант 11

x	0,25		1,75	2,5	3,25
y	3,80176	1,25	-9,0361	-17,406	29,4541
x1=0,5		x2=3

Вариант 12

x	-0,5		0,5		1,5
y	4,875		3,625		1,375	-2
x1=0,25	x2=1,75

Задание 2.Протабулировать функцию f(x) на интервале [0, 3] c шагом 0.5 и вычислить с помощью интерполяционного многочлена Лагранжа и сплайн-интерполяции значение в одном из узлов интерполяции и одно значение заданной функции для промежуточного значения аргумента x. Построить графики.

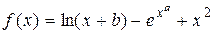
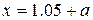, где b=№варианта, a=b/10.