Внешняя симметрия кристаллов
Кристаллы являются образованиями высокосимметричными. Элементы симметрии мы можем выделить уже при рассмотрении внешней огранки кристаллов, т.е. правильных многогранников. Отдельные части таких многогранников могут быть получены путем ряда симметричных преобразований. Простейшие симметричные преобразования следующие:
1) центросимметричное преобразование или инверсия, i ;
2) зеркальное отражение в плоскости m;
3) вращение вокруг оси, n (n=2, 3, 4, 6).
Принцип зеркального отражения в плоскости показан на рис.1.2,а, где в виде треугольников показаны какие-то части симметричной фигуры. Для построения отражения в плоскости мы из каждой точки опускаем на плоскость перпендикуляр и продолжаем его на равное расстояние по другую сторону от плоскости. Полученная точка симметрична данной.
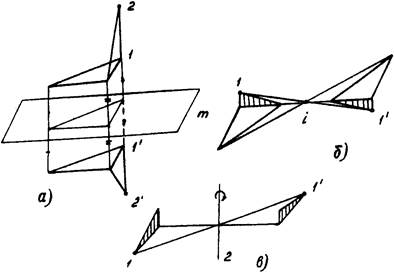
Рис.1.2. Простейшие элементы симметрии: а - плоскость зеркального отражения; б - центр инверсии; в - поворотная ось 2-го порядка.
Преобразование через центр инверсии (рис.1.2,б) состоит в том, что мы каждую точку фигуры соединяем прямой с центром i и на таком же расстоянии по другую сторону от центра строим точку, симметричную первоначальной взятой.
Поворот вокруг оси до совмещения части фигуры с симметричной ей может осуществляться на различные углы. Величина угла поворота связана с понятием порядка оси, так как порядок оси показывает сколько раз при полном повороте вокруг какой-то оси часть фигуры совпадает с ей равной. Так, на рис.1.2,в показана поворотная ось, порядок которой n=360°/180°=2.
Поворотные оси могут быть 1, 2, 3, 4 и 6-го порядков. Это справедливо только для кристаллов, так как в бесконечной структурной решетке невозможно себе представить оси 5, 7 и более высоких порядков [1].
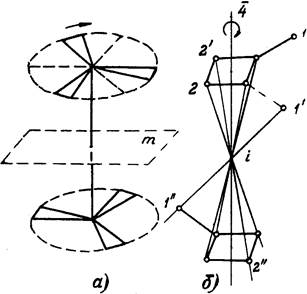
Рис.1.3. Сложные элементы симметрии: а - зеркально поворотная ось 6-го порядка; б - инверсионная ось 4-го порядка.
Легко видеть, что в каждом симметричном преобразовании участвует геометрический элемент: в первом - плоскость, во втором - точка, центр инверсии, в третьем - ось. Эти геометрические элементы называют элементами симметрии. Указанные выше плоскость, центр и ось - простейшие элементы симметрии кристаллов.
Симметричное преобразование может быть и более сложным. Например, возможен случай, когда части фигуры совпадают лишь после поворота на определенный угол, а и последующего зеркального отражения. Элемент симметрии здесь составной: совокупность поворотной оси и плоскости зеркального отражения, так называемая зеркально-поворотная ось симметрии. На рис.1.3,а показано преобразование при помощи зеркально-поворотной оси 6-го порядка. В зависимости от величины угла поворота зеркально-поворотная ось так же, как и обычная поворотная ось, может быть различного 1, 2, 3, 4 и 6-го порядка.
К сложным элементам симметрии относится также инверсионная ось симметрии. На рис.1.3,б приведено преобразование при помощи инверсионной оси 4-го порядка. Здесь суммарная операция симметрии состоит во вращении на угол j и последующей инверсии относительного центра, расположенного на оси вращения. Инверсионная ось симметрии обозначается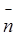 
. Реальные кристаллы могут иметь инверсионные оси симметрии только 1, 2, 3, 4 и 6-го порядков.
Рассмотренные нами элементы симметрии (плоскость симметрии, инверсия, поворотные, инверсионные оси и др.) встречаются у многогранников и в свое время были использованы для изучения внешней формы - огранки кристаллов.