Методика измерения электрических величин

Измерения подразделяют на прямые и косвенные. В случае прямого измерения искомое значение находят непосредственно как показание измерительного прибора. При косвенных измерениях искомое значение физической величины находят на основании известной математической зависимости между искомой величиной и величинами, получаемыми прямыми измерениями. Например, сопротивление резистора R находят по измерениям напряжения U и тока I, используя закон Ома:

.

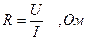Включение измерительных приборов в цепь приводит к определённому изменению режима работы (тока, напряжения и др. параметров) и, как следствие, к соответствующей погрешности измерения. В Electronics Workbench измерительные приборы идеальные, т.е. считают, что амперметры имеют нулевое сопротивление, вольтметры - бесконечно большое, что исключает или делает незначительной погрешность измерения.

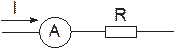
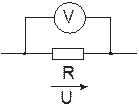
а) б)

Рис. 1.2

По данным непосредственного измерения тока I в элементе цепи (нагрузке) и напряжения на нем U легко определить мощность, как:

.

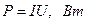В цепях переменного тока активная мощность зависит не только от напряжения и тока, но и от сдвига фаз между ними φ, т.е.

.

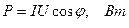Содержание работы

1. В качестве закрепления материала, полученного при изучении данной лабораторной работы, студентам предлагается на основании теоретических материалов лекции разработать и смоделировать либо использовать предлагаемую преподавателем электрическую схему на постоянном и переменном напряжении.

2. Подобрать элементы и их номиналы величин и пояснить свой выбор.

Контрольные вопросы

1. Какова область применения электроизмерительных приборов?

2. Чем отличается прямое измерение от косвенного?

3. Какие требования следует предъявлять к измерительному прибору при выборе его для измерения?

4. Начертите схему включения амперметра, вольтметра.

5. Как можно измерить сопротивление цепи, пользуясь амперметром и вольтметром?

6. Как можно косвенным путем рассчитать сопротивление цепи, пользуясь данными о токе и мощности цепи?

7. Как изменится ток в цепи, если вольтметр включить последовательно с нагрузкой?

Лабораторная работа № 2

Непосредственное применение законов Кирхгофа

Для расчета электрической цепи

Цель работы: опытным путем проверить классический метод решения электрических цепей.

Общие сведения

При расчете электрических цепей вначале необходимо определить токи в ветвях, затем приступать к расчету недостающих параметров цепи. Для этого первым шагом при расчете электрической цепи становится задание произвольного направления токов в ветвях. Метод непосредственного применения законов Кирхгофа (классический метод) основан на применении к сложным электрическим схемам 1-го и 2-го законов Кирхгофа.

Число рассчитываемых токов равно числу ветвей – А, число узлов – Б. Для расчета А неизвестных необходимо составить А уравнений. По первому закону Кирхгофа составляется (Б-1) уравнения, недостающее число уравнений (А-(Б-1)) составляют по второму закону Кирхгофа.

Решая систему из А уравнений, можно определить токи по ветвям. Если в какой-либо ветви ток оказался отрицательным, это означает, что движение тока противоположно выраженному первоначально направлению.

Формулировка первого закона Кирхгофа: алгебраическая сумма токов в узле равна нулю

.

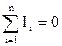При этом токи, направленные к узлу, берутся со знаком «+», а токи, направленные от узла, берутся со знаком «-».

Формулировка второго закона Кирхгофа: алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС в этом же контуре

,

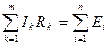где m – число пассивных элементов, на которых происходит падение напряжений в контуре;

n – число ЭДС в этом же контуре.

Для составления уравнений по второму закону Кирхгофа задают направление обхода контура, при этом совпадающие по направлению ЭДС и токи берутся со знаком «+», а противоположно направленные со знаком «- ».

Расчет и построение потенциальной диаграммы. Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. Для выполнения расчета потенциальной диаграммы (направление и величина токов должны быть уже рассчитаны) одну из точек φ выбранного контура заземляют. По оси абсцисс на графике откладывают в масштабе сопротивления вдоль контура, начиная от какой-нибудь произвольной точки, а по оси ординат - соответствующие потенциалы точек контура. Каждой точке контура цепи соответствует своя точка на потенциальной диаграмме. Следует отметить два фактора, которые учитывают при расчете потенциалов:

1) ток движется от точки с большим потенциалом к точке с меньшим потенциалом;

2) на концах источника питания происходит скачок потенциала, причем на острие потенциал выше, чем на тупой стороне стрелки источника питания.

В качестве примера рассмотрим схему (рис. 2.1). Задав направления токов и обхода контуров для расчета токов, приступим к составлению уравнений по законам Кирхгофа. Число узлов в представленной схеме равно 4, число ветвей - 6, соответственно для нахождения неизвестных токов нужно составить шесть уравнений. При этом для узлов по первому закону Кирхгофа составляется (4-1) – уравнений, для узлов 1,2 и 3.

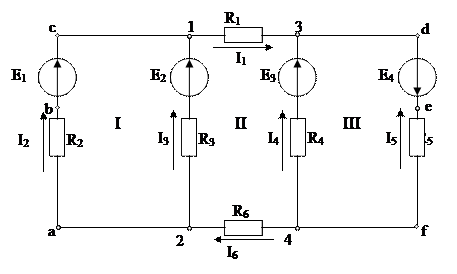
Рисунок 2.1

≠{

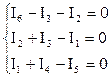
по второму закону Кирхгофа (6-(4-1)) уравнений для замкнутых контуров I, II, III.

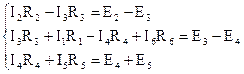
Для расчета и построения потенциальной диаграммы выберем внешний контур (рис. 2.1).

Потенциал точки а заземляем, соответственно напряжение в этой точке равно нулю φ_а= 0. Тогда:

φ_b = φ_а - I₂R₂

φ_c = φ_b + E₂

φ_d = φ_c - I₁R₁

φ_e = φ_d + E₅

φ_f = φ_e - I₅R₅

φ_a= φ_f - I₆R₆

Потенциальная диаграмма по данным расчета показана на рисунке 2.2. Угол наклона графика на каждом участке характеризует величину тока на этом участке: чем круче, тем больше ток.

Рисунок 2.2 Потенциальная диаграмма

Содержание работы

В электрической цепи:

1) измерить ток на резисторах;

2) измерить распределение потенциалов вдоль контура;

3) по экспериментальным данным проверить первый и второй законы Кирхгофа;

4) построить потенциальную диаграмму.