Лабораторная работа № 6. Последовательное соединение R, L, C элементов

Последовательное соединение R, L, C элементов

Цель работы: провести анализ цепи содержащей последовательное соединение R, L, C элементов, практически исследовать резонанс напряжений, изучить построение векторных диаграмм.

Общие сведения

Основной задачей при анализе цепи синусоидального тока является расчет тока по заданному напряжению на зажимах цепи и параметрам элементов цепи. К зажимам цепи последовательно соединенных R, L и C элементов прилагаем синусоидальное напряжение (рис. 6.1) 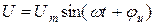. По замкнутой цепи протекает синусоидальный ток i.

Рисунок 6.1

К зажимам цепи последовательно соединенных R, L и C элементов прилагаем синусоидальное напряжение (рис. 6.1) 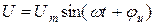. По замкнутой цепи протекает синусоидальный ток i.

По второму закону Кирхгофа напишем уравнение электрического состояния цепи:

U=U_r+U_L+U_C ,

где

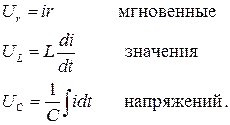
Тогда 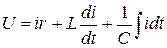. [6.1]

Уравнение [6.1] является линейным и его общий интеграл равен сумме частного решения заданного уравнения и решения соответствующего однородного уравнения при U=0.

Тогда решение будет иметь следующий вид:

.

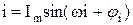Таким образом, задача сводится к определению I_m и φ (где φ=φ_u-φ_i). Проще и нагляднее задача решается с помощью векторной диаграммы (рис. 6.2), изображающей синусоидальные функции с помощью комплексных чисел.

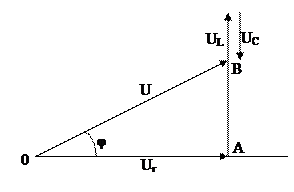
Рисунок 6.2

Ход построения векторной диаграммы следующий:

Откладываем в произвольном направлении вектор тока i. Затем относительно вектора тока I, с учетом сдвига по фазе, откладываем вектора напряжений на каждом элементе в соответствии с расположением их на схеме.

Вектор 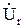совпадает по направлению с вектором тока I. Вектор 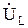опережает по фазе вектор тока на π/2, а вектор 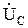отстает от вектора I на π/2.

Сумма векторов должна удовлетворять равенству U=U_r+U_L+U_C.

Из прямоугольного треугольника ОАВ, по второму закону Кирхгофа, уравнение цепи (рис 6.1) будет иметь вид:

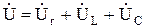, [6.2]

где , , .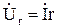

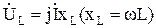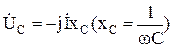После подстановки в уравнение [6.2] имеем:

.

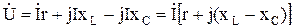Применив закон Ома, можно определить полное сопротивление цепи z:

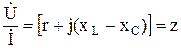, [6.3]

где 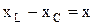- реактивное сопротивление цепи;

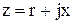- алгебраическая форма полного комплексного сопротивления цепи;

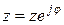показательная форма,

где 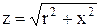, а .

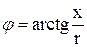В зависимости от величины реактивного сопротивления различают три режима:

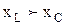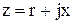1. Если , то - цепь активно-индуктивная.

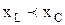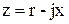2. Если , то - цепь активно-емкостная.

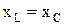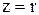3. Если , то - цепь активная.

Резонанс напряжений

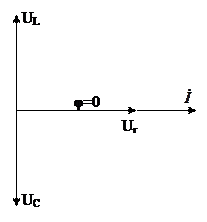
Рисунок 6.3

Если 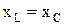, то ток в цепи 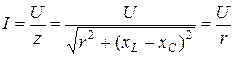, то есть цепь в данном случае имеет наименьшее сопротивление, как будто в цепи присутствует только активная нагрузка r. При этом напряжения на индуктивности и емкост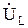и и 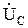сдвинуты по фазе на π и полностью компенсируют друг друга (рис. 6.3).

Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, и ток совпадает по фазе с напряжением. При этом напряжение на индуктивности 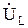и емкости 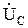может значительно превышать входное напряжение 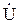, поэтому резонанс получил название резонанса напряжений.

Отношение 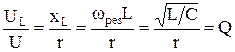выражает добротность контура. Добротность контура показывает, во сколько раз напряжение на индуктивном элементе превышает напряжение на входе схемы двухполюсника. В радиотехнике Q может доходить до 300 и более. Чем больше добротность, тем более острую форму имеют кривые тока и напряжений.

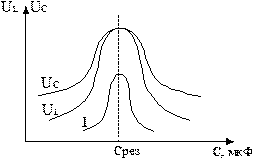
Рисунок 6.4

Из условия 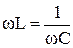следует, что резонанса напряжений можно достичь, изменяя либо частоту приложенного напряжения, либо параметры цепи - индуктивность или емкость. Угловая частота ω_рез, при которой наступает резонанс, называют резонансной угловой частотой: 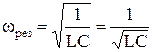. В лаборатории резонанса напряжений достигают при ω=const, L=const, изменяя емкость С (рис. 6.4). Программа EWB позволяет наблюдать резонанс, меняя любой из перечисленных параметров.

При резонансе напряжений можно отметить следующие моменты:

1. Резонанс напряжений происходит при условии, что входное сопротивление является чисто активным, т.е.: 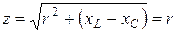, при 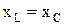. Ток и напряжение совпадают по фазе.

2. Резонанс зависит от L, C и ω. 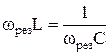, или .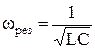

3. Напряжение источника и падение напряжения на r равны, тогда 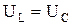, ( 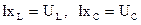) они находятся в противофазе и взаимно компенсируют друг друга .

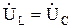Содержание работы

1. Добиться резонанса напряжения, изменяя следующие параметры:

а) угловую частоту;

б) конденсатор;

в) катушку индуктивности.

2. Показать зависимость резонансных кривых тока и напряжения от изменяемых параметров.

3. По результатам п.1 для каждого из изменяемых параметров построить векторные диаграммы для трех режимов:

а) до резонанса;

б) при резонансе;

в) после резонанса.

4. На основании проведенного опыта сделать выводы.