Основные виды алгоритмов функционирования
На первом этапе развития техники управления использовался практически лишь один вид алгоритмов функционирования — поддержание заданного постоянного значения регулируемой величины. Долгое время под системами автоматического регулирования понимался именно этот вид.
Стабилизация. Системы поддержания постоянства управляемой величины называют также системами стабилизации. Алгоритм функционирования в них имеет вид 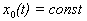 .
.
Известна важная особенность систем регулирования по отклонению: если в них использовать регуляторы, состоящие только из элементов, осуществляющих обычные аналитические преобразования, т. е. обладающих, аналитическими статическими характеристиками, то регулирование по отклонению может уменьшить, но не устранить ошибку.
Рассмотрим схему с простейшими линейными преобразовательными звеньями. Уравнения статики для такой схемы (рис. 1.2,г) будут
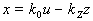 ,
, 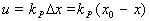 , (1.4),
, (1.4),
где 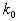 ,
, 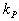 и
и 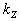 — постоянные коэффициенты, называемые соответственно коэффициентами передачи объекта, регулятора и нагрузки. Из (1.4) получаем
— постоянные коэффициенты, называемые соответственно коэффициентами передачи объекта, регулятора и нагрузки. Из (1.4) получаем
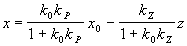 ,
,
т.e. значение регулируемой величины x зависит от нагрузки z, уменьшаясь с ее ростом.
Регулирование, в котором величина установившейся ошибки при постоянном заданном значении 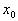 зависит от величины нагрузки z, называют статическим. Установившаяся статическая ошибка
зависит от величины нагрузки z, называют статическим. Установившаяся статическая ошибка
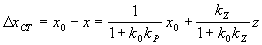 . (1-5)
. (1-5)
Статический регулятор поддерживает постоянное значение регулируемой величины с ошибкой. Статизм — это величина относительной статической ошибки при изменении нагрузки от холостого хода до номинальной. В некоторых системах статическая ошибка нежелательна. Тогда переходят к регулированию, в котором она в силу структуры системы равна нулю, т.e. к астатическому регулированию. Для этого в цепь регулирования вводят астатическое звено. Примером астатического звена является интегрирующее звено, описываемое уравнением 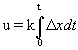 или
или 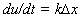 . В самом деле, регулятор при этом будет находиться в равновесии только в том случае, когда
. В самом деле, регулятор при этом будет находиться в равновесии только в том случае, когда 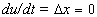 , т.е. регулируемая величина, будет равна заданному значению. Электрический двигатель является примером астатического звена.
, т.е. регулируемая величина, будет равна заданному значению. Электрический двигатель является примером астатического звена.
Программное управление. При программном управлении алгоритм функционирования задан и можно построить специальное устройство — датчик программы — вырабатывающее 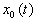 . Таким образом, все схемы, показанные на рис. 1.2, в которых
. Таким образом, все схемы, показанные на рис. 1.2, в которых 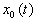 есть заданная функция, а звенья представляют собой датчики программы, вырабатывающие эту функцию, относятся к классу систем программного управления. Программное управление может осуществляться по любому из фундаментальных принципов или с помощью их комбинации.
есть заданная функция, а звенья представляют собой датчики программы, вырабатывающие эту функцию, относятся к классу систем программного управления. Программное управление может осуществляться по любому из фундаментальных принципов или с помощью их комбинации.
В практике используют два вида систем программного управления: системы с временной программой и системы с пространственной программой. В системах первого вида датчик программы вырабатывает непосредственно функцию 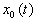 . К таким системам относят устройства для изменения температуры закалочных печей, заводные игрушки, магнитофоны, проигрыватели и т. д. Системы второго вида используют в программном управлении металлообрабатывающими станками. В них движение исполнительного органа (инструмента) осуществляется по заданной в пространстве траектории, закон же движения по траектории во времени мало существен и в широких пределах может быть произвольным.
. К таким системам относят устройства для изменения температуры закалочных печей, заводные игрушки, магнитофоны, проигрыватели и т. д. Системы второго вида используют в программном управлении металлообрабатывающими станками. В них движение исполнительного органа (инструмента) осуществляется по заданной в пространстве траектории, закон же движения по траектории во времени мало существен и в широких пределах может быть произвольным.
Следящие системы. В следящих системах алгоритм функционирования заранее неизвестен. Обычно регулируемая величина в таких системах должна воспроизводить изменение некоторого внешнего фактора, следить за ним. Так, автоматически управляемое зенитное орудие должно поворачиваться, следя за полетом цели. Следящая система может быть выполнена в соответствии с любым фундаментальным принципом управления и будет отличаться от соответствующей системы программного управления тем, что вместо датчика программы в ней будет помещено устройство слежения за изменениями внешнего фактора.
Системы с поиском экстремума показателя качества. В ряде процессов показатель качества или эффективности процесса может быть выражен в каждый момент времени функцией текущих координат системы. Управление можно считать оптимальным, если оно обеспечивает поддержание этого показателя в точке максимума, например настройка радиоприемника на частоту передающей станции по наибольшей громкости приема или по наибольшей яркости свечения индикаторной лампочки.
Для поиска экстремума необходим чувствительный элемент, обнаруживающий экстремум. Один из способов обнаружения экстремума функции одной переменной 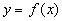 состоит в измерении частной производной
состоит в измерении частной производной 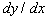 . Необходимые и достаточные условия экстремума выражены соотношениями:
. Необходимые и достаточные условия экстремума выражены соотношениями:
| для максимума | для минимума |
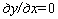  | 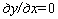  |
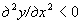  | 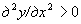 |
Для измерения 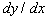 часто используют измерение в достаточно близких смежных точках разностей
часто используют измерение в достаточно близких смежных точках разностей 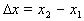 ,
, 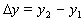 и вычисление их отношения
и вычисление их отношения 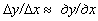 . Вместо трудно реализуемого технического измерения второй производной чаще всего делают проверку знака величины Dу в окрестности предполагаемого экстремума: Dу должно быть положительным в окрестности минимума и отрицательным в окрестности максимума. Однако одиночной проверкой можно пользоваться лишь в том случае, если известно, что экстремум существует, что он единственный и что в рабочей области нет точек перегиба функции. Если одно из этих условий не выполняется, поиск усложняется.
. Вместо трудно реализуемого технического измерения второй производной чаще всего делают проверку знака величины Dу в окрестности предполагаемого экстремума: Dу должно быть положительным в окрестности минимума и отрицательным в окрестности максимума. Однако одиночной проверкой можно пользоваться лишь в том случае, если известно, что экстремум существует, что он единственный и что в рабочей области нет точек перегиба функции. Если одно из этих условий не выполняется, поиск усложняется.
Оптимальное управление. Принцип оптимального управления в последние годы начали применять как в технических системах для повышения эффективности производственных процессов, так и в системах организационного управления для совершенствования деятельности предприятий, организаций, отраслей народного хозяйства.
В организационных системах обычно интересуются конечным установившимся результатом команды, не исследуя эффективность во время переходного процесса между отдачей команды и получением окончательного результата. Объясняется, это тем, что обычно в таких системах потери в переходном процессе достаточно малы и несущественно влияют на общую величину выигрыша в установившемся режиме, поскольку сам установившийся режим значительно более длителен, чем переходный процесс. Но иногда динамика не исследуется из-за математических трудностей. Методам оптимизации конечных состояний в организационных и экономических системах посвящены курсы методов оптимизации и исследования операций.
В управлении динамическими техническими системами оптимизация часто существенна именно для переходных процессов, в которых показатель эффективности зависит не только от текущих значений координат (как в экстремальном управлении), но также от характера их изменения в прошлом, настоящем и будущем, и выражается некоторым функционалом от координат, их производных и, может быть, времени.
Нахождение оптимального управления в подобных динамических задачах требует решения в процессе управления достаточно сложной математической задачи методами вариационного исчисления или математического программирования в зависимости от вида математического описания (математической модели) системы. Таким образом, органической составной частью системы оптимального управления становится счетно-решающее устройство или вычислительная машина. Оптимальные системы могут быть как разомкнутыми, так и замкнутыми.
Адаптивные системы. В реальных условиях внешние возмущения иногда приводят к изменению не только координат, но и параметров системы (коэффициентов уравнений), причем в таких системах, как баллистические ракеты, изменения параметров весьма существенны. Изменения параметров, вышедшие за определенные границы, приводят не только к количественным ошибкам или к ухудшению других показателей качества системы, но часто и к полной потере ее работоспособности. Эти потери качества невозможно устранить, находясь в рамках первоначально принятого принципа управления, это можно сделать лишь путем изменения параметров (а иногда и структуры) системы так, чтобы приблизить математическое описание претерпевшей изменения системы к ее исходной модели.
Системы, автоматически изменяющие значения своих параметров или структуру при непредвиденных изменениях внешних условий на основании анализа состояния или поведения системы так, чтобы сохранялось заданное качество ее работы, называют адаптивными.
Адаптивные системы с изменением значений параметров называют самонастраивающимися, с изменением структуры и алгоритма управления—самоорганизующимися.
Адаптивным системам также задают требования к качеству. Обычно адаптивная система содержит в качестве “ядра” схему, реализующую один из фундаментальных принципов управления, а контур адаптации пристраивают к ней как вторичный, осуществляющий коррекцию параметров.
