Лабораторная работа №2. Лабораторный практикум
Лабораторный практикум
По дисциплине
Алгоритмические языки и программирование
(2 семестр, С++)
Г
Оглавление
Общие указания к выполнению лабораторных работ.. 3
Лабораторная работа №1. 4
Лабораторная работа №2. 9
Лабораторная работа №3. 14
Лабораторная работа №4. 16
Приложения.. 22
Приложение Б. 35
«Функции стандартной библиотеки». 35
Особенности работы в интегрированной среде Visual C++. 41
Случайные числа. 42
Примеры программ.. 43
Общие указания к выполнению лабораторных работ
Получив вариант задания, студент знакомится с порядком выполнения работы, продумывает алгоритмы решения поставленных задач и пишет необходимые программы. Подготовленный материал предъявляется преподавателю, который после собеседования принимает решение о допуске студента к работе.
Выполнив лабораторную работу, необходимо оформить отчет, который состоит из следующих разделов:
1. Тема и цель работы.
2. Номер варианта.
3. Условия задания.
4. Текст программы с необходимыми комментариями.
5. Описание контрольного теста.
6. Результаты выполнения программы.
7. Выводы.
При защите отчета необходимо ответить на контрольные вопросы и пояснить принцип работы программы.
Лабораторная работа №1
Программирование алгоритмов линейной и разветвляющейся структуры. Организация циклов в программе. Составление выражений
Цель работы
Изучение правил построения арифметических, логических и др. выражений, применения разного рода операций языка, правил преобразования типов при выполнении арифметических операций. Освоение операторов языка для управления выполнением программы: условного, перехода, продолжения, оператора множественного выбора, операторов организации циклов.
Постановка задачи
1. Вычислить значение выражения при различных вещественных типах данных (float и double). Вычисления следует выполнять с использованием промежуточных переменных и без них. Сравнить и объяснить полученные результаты.
2. Вычислить значения выражений на бумаге и с помощью среды разработки. Объяснить полученные результаты.
Варианты
| № | Задание 1 | Задание 2 |
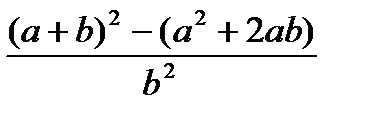 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n+++m 2) m-- >n 3) n-- >m | |
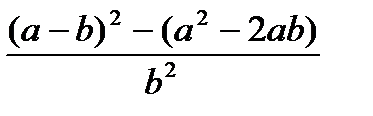 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) ++n*++m 2) m++<n 3) n++>m | |
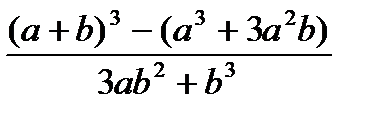 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n---m 2) m--<n 3) n++>m | |
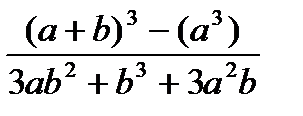 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n++*m 2) n++<m 3) m-- >m | |
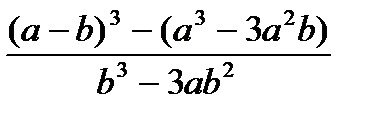 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) - -m-++n 2) m*n<n++ 3) n-- > m++ | |
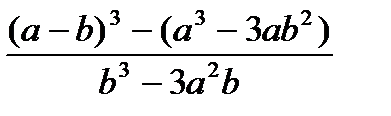 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) m-++n 2) ++m>--n 3) --n<++m | |
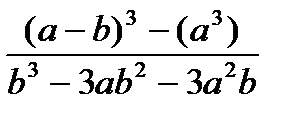 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) m+--n 2) m++<++n 3) n--< --m | |
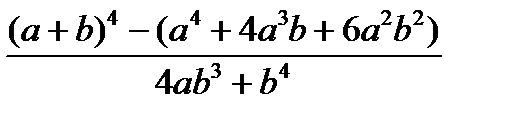 , при а=100, b=0.001 , при а=100, b=0.001 | 1) n++-m 2) m-- >n 3) n-- >m | |
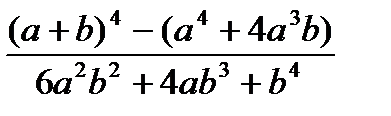 , при а=100, b=0.001 , при а=100, b=0.001 | 1) ++n*++m 2) m++<n 3) n++>m | |
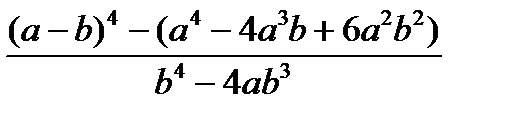 , при а=100, b=0.001 , при а=100, b=0.001 | 1) n---m 2) m--<n 3) n++>m | |
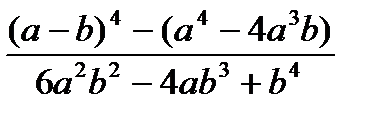 , при а=100, b=0.001 , при а=100, b=0.001 | 1) n++*m 2) n++<m 3) m-- >m | |
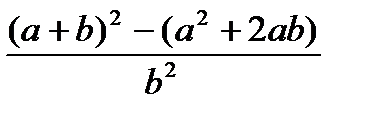 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) - -m-++n 2) m*n<n++ 3) n-- > m++ | |
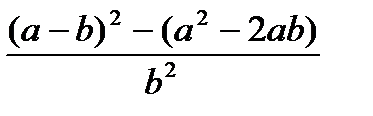 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) m-++n 2) ++m>--n 3) --n<++m | |
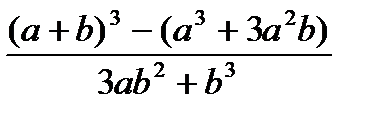 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) m+--n 2) m++<++n 3) n--< --m | |
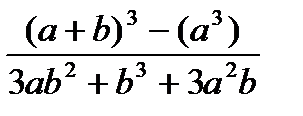 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n++-m 2) m-- >n 3) n-- >m | |
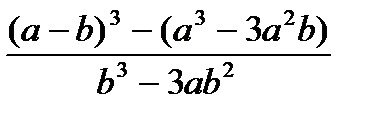 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) ++n*++m 2) m++<n 3) n++>m | |
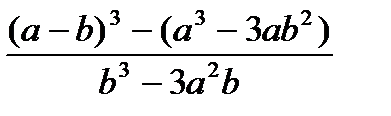 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n---m 2) m--<n 3) n++>m | |
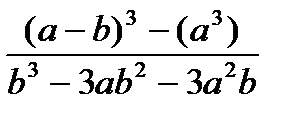 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n++*m 2) n++<m 3) m-- >m | |
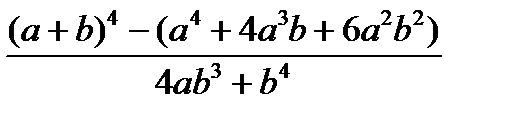 , при а=100, b=0.001 , при а=100, b=0.001 | 1) - -m-++n 2) m*n<n++ 3) n-- > m++ | |
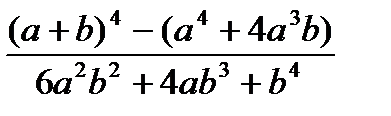 , при а=100, b=0.001 , при а=100, b=0.001 | 1) m-++n 2) ++m>--n 3) --n<++m | |
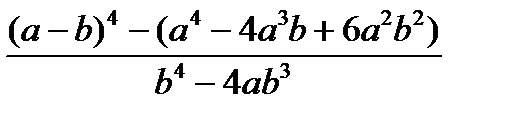 , при а=100, b=0.001 , при а=100, b=0.001 | 1) n++-m 2) m-- >n 3)n-- >m | |
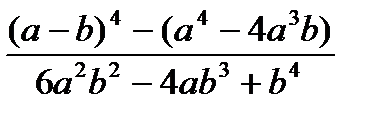 , при а=100, b=0.001 , при а=100, b=0.001 | 1) ++n*++m 2) m++<n 3) n++>m | |
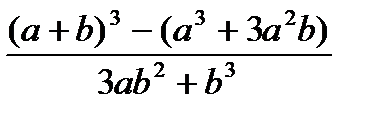 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n---m 2) m--<n 3) n++>m | |
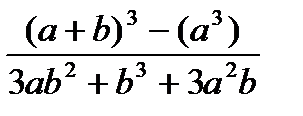 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) n++*m 2) n++<m 3) m-- >m | |
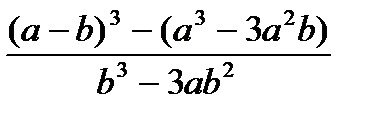 , при а=1000, b=0.0001 , при а=1000, b=0.0001 | 1) - -m-++n 2) m*n<n++ 3) n-- > m++ |
Задание 3
Составить блок-схему и написать программу для вычисления значений функции при заданных значениях аргумента.
| Номер | Вид вычисляемой функции | Исходные данные |
| 1. | 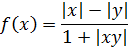 | x = 0, 5, 10 y= 1, 0, 10 |
| 2. | 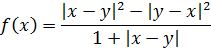 | x = 0, 5, 10; y= -1, 0, 1. |
| 3. | 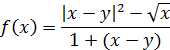 | x = 0, 5, 10; y = -1, 0, 1. |
| 4. | 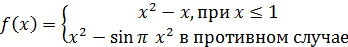 | для хÎ [0;10]; h=2 – шаг изменения переменной х. |
| 5. | 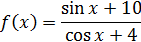 | для хÎ [0;10]; h=2 – шаг изменения переменной х. |
| 6. | 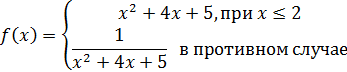 | для хÎ [0;5]; h=0.5 – шаг изменения переменной х. |
| 7. | 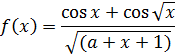 | x = 0.3, 0.8 a = 5 |
| 8. | 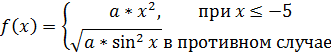 | x = -7.5, 3 a = -2.5 |
| 9. | 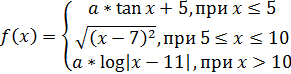 | a = -1.2 x = 4.1, 6, 9.9, 12.5 |
| 10. | 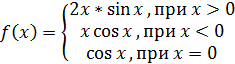 | 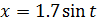 , где t = 2.0, 0, -1.2 , где t = 2.0, 0, -1.2 |
Задание 4
| Номер | Содержание |
| 1. | Найти сумму: 1)целых положительных четных чисел, меньших 100. 2) целых положительных нечетных чисел, меньших 200. 3) целых положительных чисел, больших 20, меньших 100 и кратных 3. |
| 2. | Найдите все трехзначные числа, кратные 15, но не кратные 30. |
| 3. | Требуется напечатать таблицу умножения, m×n для m от 1 до 6 и для n от 1 до 6. |
| 4. | Найти все трехзначные числа, равные сумме кубов своих цифр. |
| 5. | Напечатать все четырехзначные натуральные числа, в десятичной записи которых: 1) нет двух одинаковых цифр; 2) есть три одинаковые цифры. |
| 6. | Написать программу нахождения всех натуральных чисел на заданном интервале, являющихся полными квадратами. |
| 7. | Написать программу, определяющую, является ли заданная последовательность чисел упорядоченной . |
| 8. | Определить количество счастливых автобусных билетов. |
| 9. | Написать программу, определяющую, является ли заданная последовательность чисел геометрической прогрессией. |
| 10. | Дано натуральное число n. Определить, является ли это число палиндромом (перевертышем). |
Методические указания
Для выполнения лабораторной работы необходимо знать структуру программы на языке С/С++, базовые типы данных, правила составления выражений, использования операций, математических функций. Изучить элементарные средства программирования: для ввода-вывода данных, организации переходов и циклов в программе, приоритеты операций.
Для использования математических функций библиотеки С++ необходимо подключить к программе заголовочный файл <cmath>.
Для ввода и вывода данных использовать операции >> и << и стандартные потоки cin и cout.
Для вычисления степени использовать функцию pow(x,y) из библиотечного файла сmath.
При выполнении задания 1 использовать вспомогательные переменные для хранения промежуточных результатов.
Например: c=pow(a,3); d= pow(a+b,3); e=3*a;
Содержание отчета
1. Постановка задачи.
2. Программа решения задания1.
3. Результаты работы программы для данных типа float.
4. Результаты работы программы для данных типа double.
5. Объяснение результатов.
6. Программа решения задания2.
7. Результаты работы программы.
8. Объяснение результатов.
и т.д.
Лабораторная работа №2
Работа с массивами. Одномерные статические массивы. Многомерные динамические массивы
Цель работы
Изучение способов определения и обработки одномерных и многомерных массивов. Освоение двух форм выделения памяти под массив: статического и динамического, правил использования указателей для доступа к элементам массива.
Задание 1
| № варианта | Задание |
| 1. | Определить в программе одномерный массив Х размера n. Сформировать из него 4 массива. Первый должен содержать записанные подряд положительные элементы массива Х. Второй - отрицательные элементы массива Х. Третий - подряд запиcанные индексы элементов первого массива, которые они имели в массиве Х. Четвертый cодержит подряд записанные индексы элементов второго массива, которые они имели в массиве Х. |
| 2. | В одномерном массиве D размера n, значения элементов которого вводятся с клавиатуры, определить количество элементов, которые входят в массив более, чем по одному разу. |
| 3. | Найти минимальный среди положительных элементов определенного в программе одномерного массива Х размера n. Вывести на печать индексы отрицательных элементов массива, а также индекс минимального элемента. |
| 4. | Дан одномерный массив Y размера n. Все положительные элементы массива возвести в квадрат, а отрицательные в куб. Отпечатать старый и новый массив, а также сумму элементов в старом и новом массиве отдельно. |
| 5. | Переставьте элементы одномерного массива в обратном порядке. Нового массива не заводить. |
| 6. | Дан одномерный массив Z размера n. Найти количество нулевых элементов в массиве, сами нулевые элементы заменить на единицу, их порядковые номера записать подряд в массив В. |
| 7. | Из исходного одномерного массива А размера n образовать два массива. В первый массив войдут подряд все четные элементы массива А, во второй массив войдут подряд записанные порядковые номера четных элементов, которые они имели в массиве А. |
| 8. | Найти произведение положительных элементов одномерного массива А размера n и произведение отрицательных элементов одномерного массива В размера m. Вывести на печать наибольшее из произведений. |
| 9. | Дан одномерный массив Mas размера n. Все его элементы, не равные 0, перепишите, сохраняя их порядок, в начало массива, а нулевые – в конец массива. Нового массива не заводить. |
| 10. | В одномерном массиве D размера n, значения элементов которого вводятся с клавиатуры, найти количество соседств двух элементов разного знака. |
Задание 2
Сформировать двумерный статический массив, определить значения его элементов и выполнить задачу, указанную в соответствующем варианте.
| № варианта | Задание |
| 1. | Дана действительная матрица заданного размера. Найти сумму всех элементов, расположенных выше главной диагонали матрицы. |
| 2. | Дана целочисленная матрица заданного размера. Определить максимальный элемент и его индексы, а также минимальный элемент и его индексы. Сам максимальный элемент заменить внутри матрицы на 100, а минимальный элемент на -100. |
| 3. | Определить, есть ли в матрице заданного размера "седловые" точки. |
| 4. | Дана целочисленная матрица заданного размера. Определить, является ли она "магическим" квадратом. |
| 5. | Переверните исходную матрицу n×n относительно ее главной диагонали. Исходную и полученную матрицы выведите на экран. |
| 6. | Рассчитать «след» квадратной матрицы заданного размера. |
| 7. | Напишите программу для перестановки максимальных элементов строк числовой таблицы на главную диагональ. Элементы главной диагонали поставьте на место максимального элемента в этой строке. |
| 8. | Дана целочисленная матрица заданного размера. Определить, является ли она "латинским" квадратом. |
| 9. | Найти сумму наименьших значений элементов в столбцах действительной матрицы заданного размера. |
| 10. | В действительной матрице заданного размера произвести попарную перестановку строк, т.е. поменять местами 1 и 2 строки, 3 и 4 строки и т.д. Напечатать для сравнения обе матрицы. |
Задание 3
Затем решить задачу из задания 2, используя динамическое выделение памяти и обработку массива с применением указателей.
Методические указания к выполнению заданий
Для выполнения работы требуется знать определение массива, способы его обработки.
Массив – совокупность элементов одного типа. Многомерные массивы рассматриваются как одномерные, элементами которых являются также массивы. Нумерация элементов массива начинается с нуля.
Объявляются массивы следующим образом:
int mas[100]; // одномерный массив mas из 100 элементов
float data[10] [50];//двумерный массив data из 500 элементов
Доступ к отдельному элементу массива осуществляется указанием имени этого массива и индекса (номера) необходимого элемента, заключенного в квадратные скобки. Например:
mas[10] = 59; // десятому элементу массива mas присваивается значение 59
mas[1] = mas[0] + 1; // первый элемент массива mas на 1 больше нулевого
data[0][5] = 3.14;//пятому элементу массива data присваивается значение3.14
Инициализация массивов возможна при их определении:
double d[] = {1, 2, 3, 4, 5};
В данном случае длина массива вычисляется компилятором по количеству значений перечисленных в фигурных скобках.
Массив должен быть сначала введен в память компьютера. И ввод-вывод элементов массива, и его обработка выполняются в цикле. Для организации циклов в программе можно использовать различные операторы, в частности оператор for.
Использование датчика случайных чисел для формирования массива
Датчик случайных чисел (ДСЧ) – это программа, которая формирует псевдослучайное число. Простейший ДСЧ работает следующим образом:
Берется большое число К и произвольное 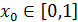 . Формируются числа х1=дробная_часть(х0*К); х2=дробная_часть(х1*К); и т. д. В результате получается последовательность чисел х0, х1, х2,. . . беспорядочно разбросанных по отрезку от 0 до 1. Их можно считать случайными, а точнее псевдослучайными. Реальные ДСЧ реализуют более сложную функцию f(x). В С++ есть функция int rand() – возвращает псевдослучайное число из диапазона 0..RAND_MAX=32767, описание функции находится в файле <stdlib.h>.
. Формируются числа х1=дробная_часть(х0*К); х2=дробная_часть(х1*К); и т. д. В результате получается последовательность чисел х0, х1, х2,. . . беспорядочно разбросанных по отрезку от 0 до 1. Их можно считать случайными, а точнее псевдослучайными. Реальные ДСЧ реализуют более сложную функцию f(x). В С++ есть функция int rand() – возвращает псевдослучайное число из диапазона 0..RAND_MAX=32767, описание функции находится в файле <stdlib.h>.
Пример формирования и печати массива с помощью ДСЧ:
#include <iostream>
using namespace std;
void main()
{
const int n=10;
int a[n];
for(int i=0;i<n;i++){
a[i]=rand()%10-5;
cout<<a[i]<<"\t";
}
}
При уменьшении или увеличении длины массива необходимо изменять его реальную длину.
Для организации динамических массивов в стиле С используются указатели и функции выделения памяти malloc(), calloc(), free() и др., а в стиле С++ для создания динамических переменных используют операцию new, определенную следующим образом:
указатель = new имя_типа[инициализатор];
где инициализатор – выражение в круглых скобках.
Операция new позволяет выделить и сделать доступным участок динамической памяти, который соответствует заданному типу данных. Если задан инициализатор, то в этот участок будет занесено значение, указанное в инициализаторе.
int*x=new int(5);
Для удаления динамических переменных используется операция delete, определенная в С++:
delete указатель;
где указатель содержит адрес участка памяти, ранее выделенный с помощью операции new.
delete x;.
Примеры:
1)int b=new int[100];//выделили в динамической памяти место под массив из 100 элементов.
2)int **matr=new int* [n];//объявляем массив указателей на строки
for(i=0;i<n;i++)
matr[i]=new int [m];//выделяем память под элементы матрицы
Указатель – это переменная, значением которой является адрес другой переменной. Объявляется указатель следующим образом:
тип *идентификатор;
инициализируется с помощью операции получения адреса &.
int x, *ptr = & x; //переменная ptr является указателем на целое и инициализируется адресом переменной x
Необходимо знать, что имя массива – это константа-указатель на начало массива (на нулевой элемент). Всякий раз, когда в выражении появляется идентификатор типа массива, он преобразуется в указатель на нулевой член массива. По определению операция индексирования [] интерпретируется таким образом, что E1[E2] идентично *((E1)+(E2)). В силу правил преобразования, применяемых к +, если E1 массив и E2 целое, то E1[E2] относится к E2-ому члену E1.
Это правило аналогичным образом применяется в случае многомерного массива. Если E является n-мерным массивом ранга i*j*...*k, то возникающее в выражении E преобразуется в указатель на (n-1)-мерный массив ранга j*...*k. Рассмотрим, например,
int x[3][5];
Здесь x - массив целых размером 3*5. Когда x возникает в выражении, он преобразуется в указатель на (первый из трех) массив из 5 целых чисел. В выражении x[i], которое эквивалентно *(x+1), x сначала преобразуется, как описано, в указатель, затем 1 преобразуется к типу x, что включает в себя умножение 1 на длину объекта, на который указывает указатель, а именно объект из 5 целых. Результаты складываются, и используется косвенная адресация для получения массива (из 5 целых), который в свою очередь преобразуется в указатель на первое из целых. Если есть еще один индекс, снова используется тот же параметр; на этот раз результат является целым.
Именно из всего этого вытекает то, что массивы в C хранятся по строкам (быстрее всего изменяется последний индекс), и что в описании первый индекс помогает определить объем памяти, поглощаемый массивом, но не играет никакой другой роли в вычислениях индекса.
Определение динамического массива из 25 целых чисел:
int *p;
int n=25;
p=(int *)malloc(n);
Обращение к нулевому элементу массива:
* p;
Обращение к i - элементу массива:
* (p + i);
Обращение к ( i , j ) - элементу двумерного массива:
p[i][j] = = *(p[i]+j) = = *(*(p+i)+j).
Пример:
int *u=(int*)malloc(sizeof(int)); // в функцию передается количество требуемой памяти в байтах, т. к. функция malloc возвращает значение типа void*, то его необходимо преобразовать к типу указателя (int*).
free(u); //освобождение выделенной памяти.
Некотрые определения
Cедловые точки матрицы – минимальный элемент в строке и максимальный в столбце.
Пример: 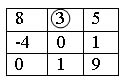
Cлед матрицы – сумма элементов на главной диагонале.
Магический квадрат –матрица n*n, где сумма элементов в строке равна сумме элементов в столбце и равна сумме элементов по диагонали.
Латинский квадрат порядка n – матрица n´n, составленная из чисел от 1 до n.
Пример: 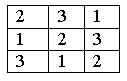
Числа армстронга: Числа, равные сумме кубов своих цифр: 153=13+53+33; 370=33+73.
Совершенное число равно сумме своих делителей исключая само число.
Дружественное число – если одно равно сумме делителей другого.
