Теория размерностей. Основные числа подобия: Рейнольдса (Re), Нуссельта (Nu), Пекле (Pe), Прандтля (Pr), Фруда (Fr), Грасгоффа (Gr), Маха (M)

В случаях, когда изучаемые процессы не описываются дифференциальными уравнениями, одним из путей их анализа является эксперимент, результаты которого наиболее целесообразно представлять в обобщенной форме (в виде безразмерных комплексов). Методом составления таких комплексов является метод анализа размерностей.

Размерность какой-либо физической величины определяется соотношением между ней и теми физическими величинами, которые приняты за основные (первичные). В каждой системе единиц имеются свои основные единицы. Например, в Международной системе единиц измерения СИ за единицы измерения длины, массы и времени соответственно приняты метр (м), килограмм (кг), секунда (с). Единицы измерения остальных физических величин, так называемых производных величин (вторичных), принимаются на основании законов, устанавливающих связь между этими единицами. Эта связь может быть представлена в виде так называемой формулы размерности.

Теория размерностей основана на двух положениях.

1. Отношение двух числовых значений какой-либо величины не зависит от выбора масштабов для основных единиц измерения (например, отношение двух линейных размеров не зависит от того, в каких единицах они будут измеряться).

2. Любое соотношение между размерными величинами можно сформулировать как соотношение между безразмерными величинами. Это утверждение представляет так называемую П-теорему в теории размерностей.

Из первого положения следует, что формулы размерности физических величин должны иметь вид степенных зависимостей

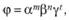
где 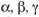– размерности основных единиц.

Допустим, что число основных размерных единиц, через которые могут быть выражены все п переменных величин, равно т. П-теорема устанавливает, что если все п переменных величин выразить через основные единицы, то их можно сгруппировать в 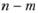безразмерных П-членов, т.е.

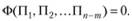
При этом каждый П-член будет содержать 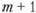переменную величину.

В задачах гидромеханики число переменных, входящих в П-члены, должно равняться четырем. Три из них будут определяющими (обычно это характерная длина, скорость течения жидкости и ее плотность) – они входят в каждый из П-членов. Одна из этих переменных (четвертая) является различной при переходе от одного П-члена к другому. Показатели степени определяющих критериев (обозначим их через х, у, z) являются неизвестными. Показатель степени четвертой переменной для удобства примем равным -1.

Соотношения для П-члснов будут иметь вид

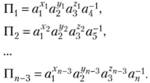
Входящие в П-члены переменные можно выразить через основные размерности. Так как эти члены являются безразмерными, то показатели степени каждой из основных размерностей должны быть равны нулю. В результате для каждого из П-членов можно составить по три независимых уравнения (по одному для каждой размерности), которые связывают показатели степени входящих в них переменных. Решение полученной системы уравнений дает возможность найти числовые значения неизвестных показателей степени х, у, z. В итоге каждый из П-членов определяется в виде формулы, составленной из конкретных величин (параметров среды) в соответствующей степени.

Критерий подобия— безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие их физического подобия. Критерии подобия, представляющие собой отношения одноимённых физических параметров системы (например, отношения длин), называются тривиальными и при установлении определяющих критериев подобия обычно не рассматриваются: равенство их для двух систем является определением физического подобия. Нетривиальные безразмерные комбинации, которые можно составить из определяющих параметров, и представляют собой критерии подобия. Всякая новая комбинация из критериев подобия также является критерием подобия, что даёт возможность в каждом конкретном случае выбрать наиболее удобные и характерные критерии. Число определяющих нетривиальных критериев подобия меньше числа определяющих физических параметров с различными размерностями на величину, равную числу определяющих параметров с независимыми размерностями (см. «Пи-теорема»).

Если известны уравнения, описывающие рассматриваемое физическое явление, то критерии подобия для этого явления можно получить, приводя уравнения к безразмерному виду путём введения некоторых характерных значений для каждого из определяющих физических параметров, входящих в систему уравнений. Тогда критерии подобия определятся как безразмерные коэффициенты, появляющиеся перед некоторыми из членов новой, безразмерной системы уравнений. Когда уравнения, описывающие физическое явление, неизвестны, критерии подобия отыскиваются при помощи анализа размерностей, определяющих физические параметры.

Число (критерий) Рейно́льдса ( 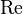), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

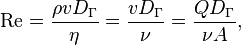
где

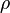• — плотность среды, кг/м³;
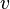• — характерная скорость, м/с;
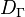• — гидравлический диаметр, м;
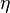• — динамическая вязкость среды, Па·с или кг/(м·с);
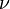• — кинематическая вязкость среды, м²/с ( );
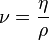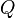• — объёмная скорость потока;
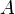• — площадь сечения трубы.

Число Нуссельта (Nu) — один из основных критериев подобия тепловых процессов, характеризующий соотношение между интенсивностью теплообмена за счёт конвекции и интенсивностью теплообмена за счёт теплопроводности (в условиях неподвижной среды). Названо в честь немецкого инженера Вильгельма Нуссельта.

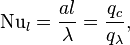^[1] где:

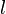• — характерный размер;
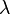• — коэффициент теплопроводности среды;
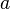• — коэффициент теплоотдачи;
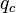• — тепловой поток за счёт конвекции;
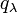• — тепловой поток за счёт теплопроводности.

Число или критерий Пекле (Ре) — критерий подобия, который характеризует соотношение между конвективным и молекулярным процессами переноса тепла (примесей, количества движения, характеристик турбулентности) в потоке жидкости (соотношение конвекции и диффузии), а также является критерием подобия для процессов конвективного теплообмена.

Используется при построении расчётных схем (метод конечных разностей, метод конечных элементов) для решения дифференциальных уравнений в частных производных, описывающих течения вязкой жидкости.

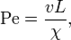
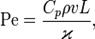
где

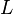— характерный линейный размер поверхности теплообмена;

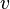— скорость потока жидкости относительно поверхности теплообмена;

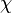— коэффициент температуропроводности;

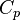— теплоёмкость при постоянном давлении;

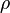— плотность жидкости;

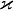— коэффициент теплопроводности жидкости.

При малых значениях 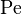преобладает молекулярная теплопроводность, а при больших — конвективный перенос теплоты.

Число Пекле связано соотношением 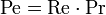с числом Рейнольдса 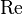и числом Прандтля .

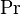Число Прандтля ( 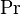) — один из критериев подобия тепловых процессов в жидкостях и газах, учитывает влияние физических свойств теплоносителя на теплоотдачу:

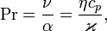где

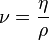— кинематическая вязкость;

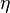— динамическая вязкость;

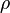— плотность;

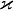— коэффициент теплопроводности;

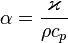— коэффициент температуропроводности;

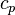— удельная теплоёмкость среды при постоянном давлении.

Число Прандтля связано с другими критериями подобия — числом Пекле 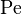и числом Рейнольдса 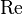соотношением .

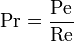Число Фруда (Fr) - характеризует соотношение между силой инерции и внешней силой, в поле которой происходит движение, действующими на элементарный объём жидкости или газа:

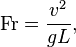
где 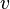— характерный масштаб скорости, — ускорение, характеризующее действие внешней силы, 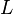— характерный размер области, в которой рассматривается течение.

Например, если рассматривается течение жидкости в трубе в поле силы тяжести, то под величиной понимается ускорение свободного падения, под величиной 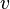— скорость течения, а за 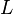можно принять длину трубы или её диаметр

Число́ Грасго́фа ( 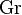) — критерий подобия, параметр подобия, безразмерная величина, определяет процесс подобия теплообмена при конвекции в поле тяжести (гравитации, ускорения) и является мерой соотношения архимедовой выталкивающей силы, вызванной неравномерным распределением плотности жидкости, газа в неоднородном поле температур, и силами вязкости.

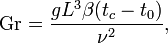где

— ускорение свободного падения, на поверхности Земли 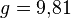м/с²;

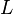— определяющий характерный линейный размер поверхности теплообмена, м;

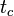— температура поверхности теплообмена, °C;

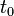— температура теплоносителя, °C;

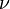— коэффициент кинематической вязкости, м²/с;

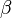— температурный коэффициент объёмного расширения теплоносителя, для газов, при не слишком большом постоянном давлении, 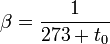К⁻¹.

Число́ Ма́ха ( 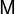) — в механике сплошных сред — один из критериев подобия в механике жидкости и газа. Представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде.

Число Маха

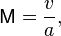
где 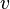— скорость потока, а 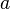— местная скорость звука,

является мерой влияния сжимаемости среды в потоке данной скорости на его поведение: из уравнения состояния идеального газа следует, что относительное изменение плотности (при постоянной температуре) пропорционально изменению давления:

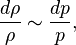
из закона Бернулли разность давлений в потоке 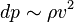, то есть относительное изменение плотности:

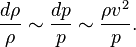
Поскольку скорость звука 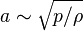, то относительное изменение плотности в газовом потоке пропорционально квадрату числа Маха:

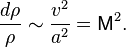
Билет №3