II. Устные упражнения. III. Тренировочные упражнения

1. Вычислить:

3. № 687, 691, 688 (а, б, в).

III. Тренировочные упражнения.

1. На доске прикреплена ромашка, на лепестках которой с обратной стороны записаны задания из № 675 (б), 676 (б), 679 (а), 679 (б), 678 (б), 677 (б), 683 и такое задание:

Выразите m из формулы а = 150 : m + 1 (всего 8 лепестков).

(4 человека вызываются к доске, после ответа одного вызываются по одному; можно включить дополнительный вопрос).

2. На повторение № 693 (б, г).

3. Самостоятельная работа на оценку:

Вариант I – № 699 (1); вычислить: (2³ + 5²) × 3.

Вариант II – № 699 (2); вычислить: (6² + 3³) : 21

IV. Итог урока.

1. Повторить все формулы.

2. Какие формулы нужно использовать при решении домашнего задания № 702, 703.

V. Домашнее задание. п. 17, повторить п. 7, 8; № 702, 703, 707 (в, г), 708 (б).

Урок № 67
Площадь. Площадь прямоугольника (п. 18, ч. 1)

Цели:сформировать понятия квадратного сантиметра, площади фигуры; научить находить площадь прямоугольника, сложной фигуры, научить определять равные фигуры.

Оборудование: квадрат со стороной 1 см; раздаточный материал (по две фигуры, разбитые на кв. сантиметры); демонстрационные равные фигуры.

Ход урока

I. Проверка домашнего задания.

Консультанты до урока проверили домашние работы у учащихся и докладывают о их выполнении.

II. Устные упражнения.

1. Восстановить цепочку вычислений.

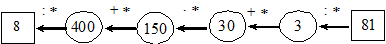
2. (70 : 5 +2) × 4 – 64 Результат разделить на 11.

(48 : 4 – 2) × 9 : 45 + 18 Результат возвести в квадрат.

3. Можно ли указать число, которое не является корнем уравнения:

а) х : х = 1; б) 0 : х = 0; в) m : 0 = 0; г) u × 1 = u?

4. Наименьшее четырехзначное число уменьшите на 100. Какой получится результат?

III. Изучение нового материала.

1) Что такое квадратный сантиметр?

2) Как найти площадь фигуры?

3) Рассмотреть примеры рис. 62, 63; найти площади фигур, лежащих на парте у учащихся.

4) S – площадь прямоугольника, а – длина, b – ширина.

S = аb.

5) Определение равных фигур (продемонстрировать).

6) Каковы площади равных фигур?

7) Чему равна площадь всей фигуры, если фигура разделена на части?

IV. Закрепление.

1. Устно № 709, 711, 712, 714.

2. № 716, 717.

3. На повторение: № 731, 732.

V. Итог урока.

Ответить на вопросы или найти в учебнике ответ на вопросы к п. 18.

VI. Домашнее задание. п. 18 (до площади квадрата); № 736, 741 (а), 744, 745.

Урок № 68

Квадрат. Формула площади квадрата (п. 18)

Цели:научить находить площадь треугольника, квадрата.

Оборудование: карточки для проверки домашнего задания; кодоскоп, пленки с устными упражнениями; пленки с рис. 64, 65; фигуры прямоугольника, квадрата, опорный конспект.

Ход урока

I. Проверка домашнего задания.

1. Проверить фронтально только ответы.

2. Площадь одного квадрата равна 1 см².

Какова площадь каждой фигуры.

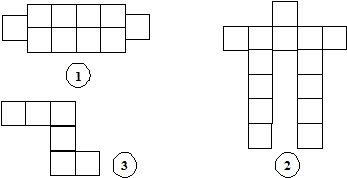
Шесть человек за первыми партами выполняют работу по карточкам.

Карточки для учащихся.

Вариант I

1) Заполните таблицу, где а и b – стороны прямоугольника.

а	b	S	Р
32 см	7 см

2) Начертите две неравные фигуры, имеющие одинаковую площадь 3 см².

Вариант II

1) Заполните таблицу, где а и b – стороны прямоугольника.

а	b	S	Р
27 см	8 см

2) Начертите две неравные фигуры, имеющие одинаковую площадь 4 см².