Сравнение бесконечно малых. Принцип эквивалентности
Определение 6.1.Бесконечно малые 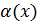 и
и 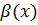 называются бесконечно малыми одного порядка, если
называются бесконечно малыми одного порядка, если 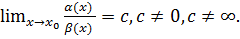
Определение 6.2.Бесконечно малые 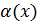 и
и 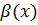 называются эквивалентными (
называются эквивалентными ( 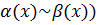 , если
, если 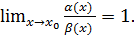
Определение 6.3.Бесконечно малая 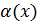 называется бесконечно малой высшего порядка (по сравнению с бесконечно малой
называется бесконечно малой высшего порядка (по сравнению с бесконечно малой 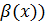 , если
, если 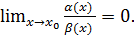
-17-
Теорема 6.1.Если 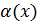 и
и 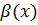 - эквивалентные бесконечно малые, то
- эквивалентные бесконечно малые, то
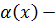
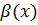 - бесконечно малая высшего порядка по сравнению с каждой из них.
- бесконечно малая высшего порядка по сравнению с каждой из них. 
Теорема 6.2.Если 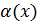 - бесконечно малая высшего порядка по сравнению с
- бесконечно малая высшего порядка по сравнению с 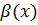 , то
, то 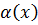
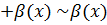 .
.
Теорема 6.3 (принцип эквивалентности).Если 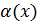 и
и 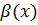 - эквивалентные бесконечно малые, то
- эквивалентные бесконечно малые, то 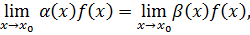
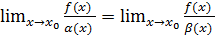 .
.
Т.е., если под знаком предела бесконечно малая входит как сомножитель, то ее можно заменить на эквивалентную.
Замечание 6.1.Особо заметим, что этого нельзя делать в разностях и суммах.
Из первого, третьего, четвёртого и пятого замечательных пределов и их следствий вытекает следующая таблица эквивалентности для бесконечно малых:
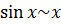 (6.1)
(6.1)
tg  (6.2)
(6.2)
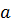 rcsin
rcsin 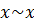 (6.3)
(6.3)
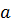 rctg
rctg  (6.4)
(6.4)
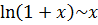 (6.5)
(6.5)
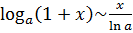 (6.6)
(6.6)
 (6.7)
(6.7)
 (6.8)
(6.8)
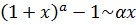 (6.9)
(6.9)
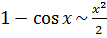 (6.10)
(6.10)
-18-
Докажем (6.10). Для этого посчитаем предел 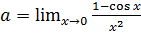 . Этот предел представляет из себя неопределённость вида
. Этот предел представляет из себя неопределённость вида 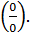 Для того, чтобы его посчитать, нужно воспользоваться формулой
Для того, чтобы его посчитать, нужно воспользоваться формулой 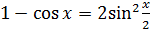 и тем, что
и тем, что 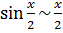 . Тогда получим:
. Тогда получим: 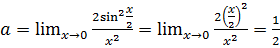 , откуда следует (6.10).
, откуда следует (6.10).
Вычисление пределов.
В этом разделе рассмотрим ряд типовых задач на вычисление пределов.
Пример 7.1. 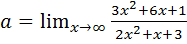 .
.
Предел 7.1 представляет из себя неопределённость вида 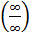 ( всюду ниже, чтобы указать вид неопределённости, мы будем просто приравнивать предел к соответствующему обозначению неопределённости).
( всюду ниже, чтобы указать вид неопределённости, мы будем просто приравнивать предел к соответствующему обозначению неопределённости).
Для вычисления подобных пределов нужно числитель и знаменатель дроби разделить на старшую степень, а затем воспользоваться теоремами 3.7, 3.3 и 3.4. Имеем:
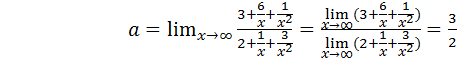 .
.
Пример 7.2. 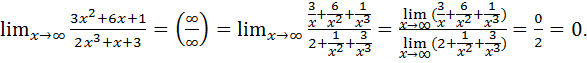
Пример 7.3. 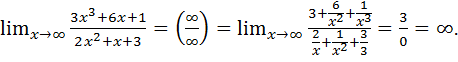
Здесь используется, что величина, обратная бесконечно малой является бесконечно большой (теорема 3.3).
Заметим, что пределы 7.2 и 7.3 можно было бы посчитать и несколько иначе:
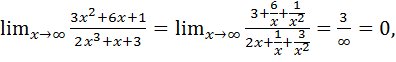 -19-
-19-
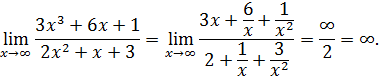
Проанализировав решения примеров7.1 – 7.3, нетрудно понять, что справедлива следующая
Теорема 7.1.Пусть 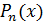 и
и 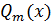 – многочлены степеней
– многочлены степеней 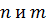 соответственно, т.е.
соответственно, т.е. 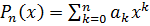 ,
, 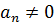 ,
, 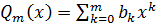 ,
, 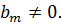 Пусть
Пусть 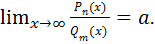 Тогда: 1) если
Тогда: 1) если 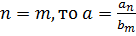 ; 2) если
; 2) если 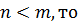
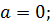 3) если
3) если 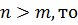
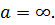
Рассмотрим теперь пределы отношений многочленов при 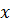 , стремящемся к конечному числу.
, стремящемся к конечному числу.
Пример 7.4. 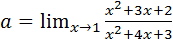 .
.
В силу теорем 4.1 и 4.2 рассматриваемая функция является непрерывной. Это означает, что 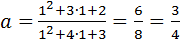 .
.
Пример 7.5. 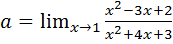 .
.
Положив 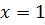 , получим, что
, получим, что 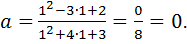
Пример 7.6. 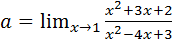 .
.
Положив 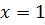 , получим, что
, получим, что 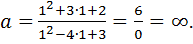
Пример 7.7. 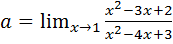 .
.
Положив 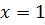 , получим, что
, получим, что 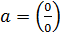 , т.е., в отличие от пределов 7.4 – 7.6, предел 7.7 является неопределённостью вида
, т.е., в отличие от пределов 7.4 – 7.6, предел 7.7 является неопределённостью вида 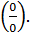 То, что при
То, что при 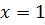 числитель и знаменатель дроби обращаются в нуль, означает. Что каждый из них разлагается на множители, один из которых равен
числитель и знаменатель дроби обращаются в нуль, означает. Что каждый из них разлагается на множители, один из которых равен 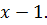 Найдя корни
Найдя корни
-20-
числителя и знаменателя, разложив последние на множители, получим:
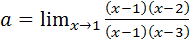
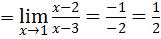 .
.
Пример 7.8. 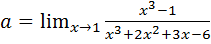 .
.
Положив 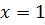 , получим, что
, получим, что 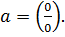 Разложим числитель по формуле разности кубов. Для разложения на множители знаменателя разделим его на
Разложим числитель по формуле разности кубов. Для разложения на множители знаменателя разделим его на 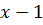 . Тогда получим:
. Тогда получим:
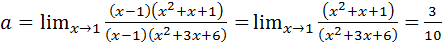 .
.
Пример 7.9. 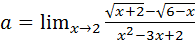 .
.
Положив 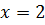 , получим:
, получим: 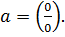 Для раскрытия этой неопределённости нужно умножить числитель и знаменатель дроби на выражение, сопряжённое числителю, т.е. на
Для раскрытия этой неопределённости нужно умножить числитель и знаменатель дроби на выражение, сопряжённое числителю, т.е. на 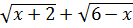 , и разложить знаменатель на множители:
, и разложить знаменатель на множители:
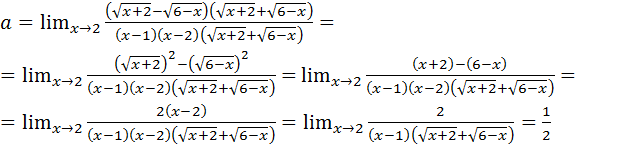 .
.
Пример 7.10. 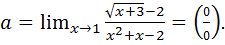
Для раскрытия неопределённости умножим числитель и знаменатель дроби на 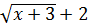 и разложим знаменатель на множители. Тогда получим:
и разложим знаменатель на множители. Тогда получим:
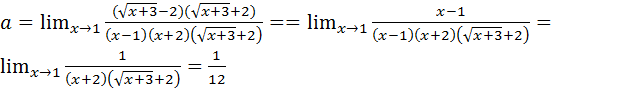 .
.
-21-
Пример 7.11. 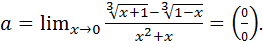
Разложив знаменатель на множители и умножив числитель и знаменатель на 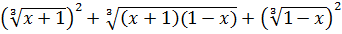 , в силу формулы разности кубов
, в силу формулы разности кубов 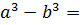
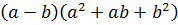 получим:
получим:
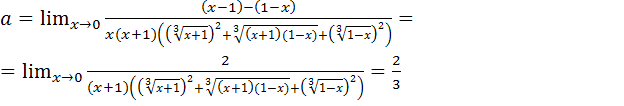 .
.
Пример 7.12. 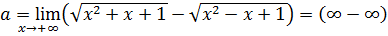 .
.
Для раскрытия неопределённости 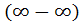 умножим и разделим на сопряженное выражение
умножим и разделим на сопряженное выражение 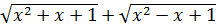 . Тогда получим:
. Тогда получим:
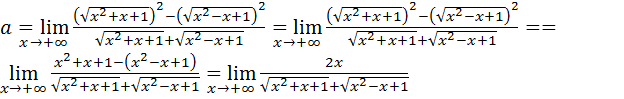 .
.
Разделив числитель и знаменатель на 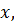 получим:
получим:
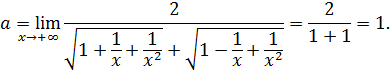
Пример 7.13. 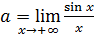 .
.
Заметим, что этот предел не имеет ничего общего с первым замечательным пределом (5.1). Поскольку 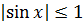 , а
, а  – бесконечно малая при
– бесконечно малая при 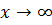 , то
, то 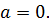
Перейдём теперь к пределам, при вычислении которых используются замечательные пределы или, что то же самое, таблица эквивалентности.
Пример 7.14. 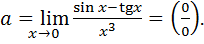
-22-
Сначала особо заметим, что если в разности, стоящей в числителе предела
7.14, 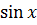 и
и 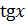 заменить на эквивалентную бесконечно малую величину
заменить на эквивалентную бесконечно малую величину 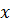 , то получится неверный ответ
, то получится неверный ответ 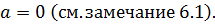
Для получения правильного ответа нужно положить 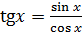 , затем вынести
, затем вынести 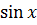 за скобки, тогда в силу (6.1) и (6.10) получим:
за скобки, тогда в силу (6.1) и (6.10) получим:
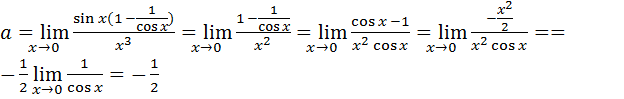 .
.
Пример 7.15. 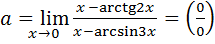 .
.
Поделив числитель и знаменатель дроби на 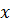 , в силу (6.3) и (6.4) получим:
, в силу (6.3) и (6.4) получим:
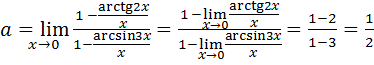 .
.
Заметим, что если в пределе 7.15 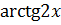 и
и 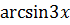 заменить на эквивалентные бесконечно малые
заменить на эквивалентные бесконечно малые 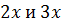 , то получится правильный ответ. Но такое решение будет неверным, так как нет теоремы, на которую можно сослаться.
, то получится правильный ответ. Но такое решение будет неверным, так как нет теоремы, на которую можно сослаться.
Пример 7.16. 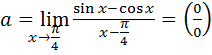 .
.
Для раскрытия неопределённости нужно разность в числителе преобразовать в произведение. Кроме того, поскольку в замечательных пределах (кроме второго в одном из видов) 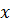 стремится к нулю, то удобно ввести новую переменную
стремится к нулю, то удобно ввести новую переменную 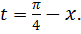 Тогда
Тогда 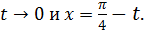 Тогда
Тогда 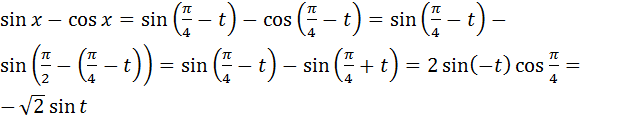 , откуда получим:
, откуда получим: 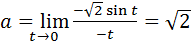 . -23-
. -23-
Пример 7.17. 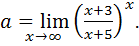
Поскольку 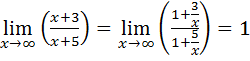 , то предел 7.17 является неопределённостью вида
, то предел 7.17 является неопределённостью вида 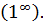 Воспользовавшись логарифмическим тождеством
Воспользовавшись логарифмическим тождеством 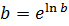 , представим основание в виде
, представим основание в виде 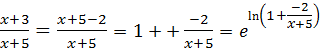 .Тогда
.Тогда 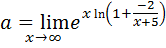 .
.
Воспользовавшись непрерывностью экспоненты (см. определение 4.1 и теорему 4.1) и тем, что если 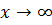 , то
, то 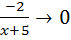 и, следовательно,
и, следовательно, 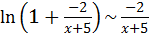 (см. (6.5)), получим:
(см. (6.5)), получим:
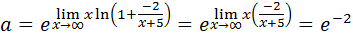 .
.
С помощью выкладок, используемых при вычислении предела 7.17, может быть доказана
Теорема 7.2.Пусть 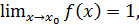
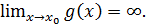 Тогда
Тогда 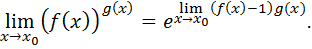
Действительно, так как 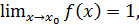 то
то 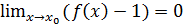 и
и 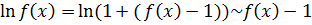 при
при 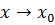 . Тогда
. Тогда
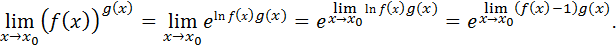
Все неопределённости вида 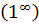 раскрываются по теореме 7.2.
раскрываются по теореме 7.2.
Пример 7.18. 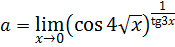 .
.
Так как 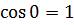 , tg
, tg 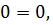 то
то 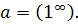
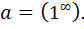 Тогда
Тогда
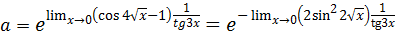 .
.
-24-
Поскольку 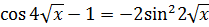 и
и 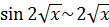 , tg3
, tg3 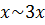 , то
, то
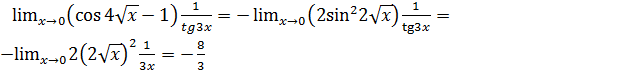 . Следовательно,
. Следовательно, 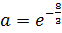 .
.
Пример 7.20. 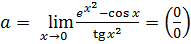 .
.
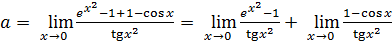 .
.
Поскольку 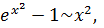
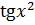
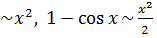 (см. (6.7), (6.2), (6.10)), то
(см. (6.7), (6.2), (6.10)), то
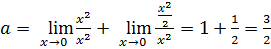 .
.
Пример 7.21. 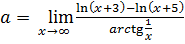 .
.
Поскольку 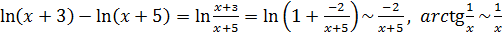 при
при 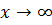 (см. (6.5) и (6.4)), то
(см. (6.5) и (6.4)), то 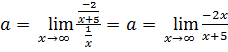 =
= 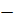 2.
2.
Пример 7.22. 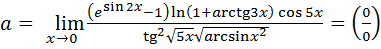 .
.
Поскольку 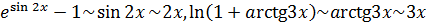 ,
,
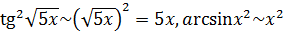 , то
, то 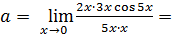
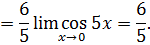
Заметим, что писать сначала 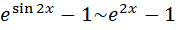 , а затем
, а затем 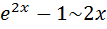
некорректно, так как не сформулированы соответствующие теоремы, на которые можно было бы сослаться. По той же причине недопустимо писать сначала 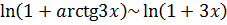 , а затем
, а затем 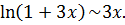
-25-
