Краткие теоретические сведения. В данной работе рассматриваются лишь модели классической экологии (взаимодействие

В данной работе рассматриваются лишь модели классической экологии (взаимодействие популяций).

Популяция ¾ совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию.

Взаимодействие особей внутри популяции определяется внутривидовой конкуренцией, взаимодействие между популяциями ¾ межвидовой конкуренцией.

Внутривидовая конкуренция в популяции с дискретным размножением.Для популяций с дискретным размножением (некоторые виды растений, насекомых и т.д.) поколения четко разнесены во времени и особи разных поколений не сосуществуют. Численность такой популяции можно характеризовать числом N_t и считать t величиной дискретной ¾ номером популяции.

Одна из моделей межвидовой конкуренции в этом случае выражается уравнением

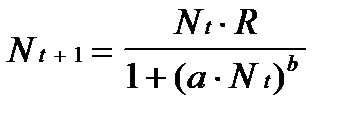(1)

Здесь R ¾ скорость воспроизводства популяции в отсутствии внутривидовой конкуренции (математически это соответствует случаю a = 0). Тогда уравнение определяет просто изменение численности популяции по закону геометрической прогрессии: 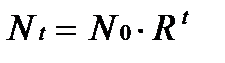, где N₀ ¾ начальная численность популяции.

Знаменатель в уравнении (1) отражает наличие конкуренции, делающей скорость роста тем меньше, чем больше численность популяции; a и b ¾ параметры модели.

Исходные параметры модели:

· R ¾ скорость воспроизводства;

· N₀ ¾ начальная численность популяции;

· a ¾ параметр, характеризующий интенсивность внутривидовой конкуренции.

Характерная черта эволюции при b=1 ¾ выход численности популяции на стационарное значение при любых значениях других параметров. Однако, в природе так бывает не всегда, и более общая модель при b¹1 отражает другие, более сложные, но реально существующие, виды эволюции. Данная модель позволяет получить четыре таких вида:

1) монотонное установление стационарной численности популяции;

2) затухающие колебания и установление стационарной численности популяции;

3) устойчивые предельные циклы изменения численности популяции;

4) случайные изменения численности популяции без наличия явных закономерностей (динамический хаос).

Внутривидовая конкуренция в популяции с непрерывным размножением.Математическая модель в данном случае строится на основе дифференциальных уравнений. Наиболее известна так называемая логистическая модель:

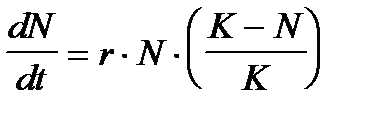(2)

Исходные параметры модели:

· r ¾ скорость роста численности популяции в отсутствие конкуренции;

· K ¾ предельное значение численности популяции, при котором скорость роста становится равной нулю;

· N₀ ¾ начальная численность популяции.

Межвидовая конкуренция.В этом случае исследуется конкуренция популяций, потребляющих общий ресурс. Пусть N₁ и N₂ ¾ численности конкурирующих популяций. Модель (называемая также моделью Лотки-Вольтерры) выражается уравнениями

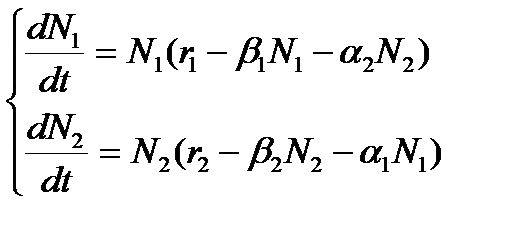(3)

Содержательный смысл параметров: r₁ и r₂ – скорости роста численности первой и второй популяций соответственно в отсутствие конкуренции; β₁ и β₂ – коэффициенты, учитывающие внутривидовую конкуренцию; a₁и a₂ отражают интенсивность межвидовой конкуренции.

Главный вопрос, который интересует исследователя межвидовой конкуренции ¾ при каких условиях увеличивается или уменьшается численность каждого вида? Данная модель предсказывает следующие режимы эволюции взаимодействующих популяций: устойчивое сосуществование или полное вытеснение одной из них.

Система «хищник-жертва».В этой системе ситуация значительно отличается от предыдущей. В частности, если в случае конкурирующих популяций исчезновение одной означает выигрыш для другой (дополнительные ресурсы), то исчезновение «жертвы» влечет за собой и исчезновение «хищника», для которого в простейшей модели «жертва» является единственным кормом.

Обозначим через С численность популяции хищника и через N ¾ популяции жертвы. Одна из известных моделей выражается следующими уравнениями:

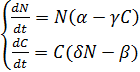(4)

В первое уравнение заложен следующий смысл. В отсутствии хищников (т.е. при С=0) численность жертв растет экспоненциально со скоростью α, т.к. модель не учитывает внутривидовой конкуренции. Число жертв уменьшается тем больше, чем чаще происходят встречи представителей видов; γ ¾ коэффициент эффективности поиска.

Второе уравнение говорит о следующем. В отсутствии жертв численность хищников экспоненциально убывает со скоростью β; положительное слагаемое в правой части уравнения компенсирует эту убыль; δ ¾ коэффициент эффективности перехода пищи в потомство хищников.