Бесконтактный электродвигатель

В приводах подачи металлообрабатывающих станков широкое применение находят бесконтактные (бесколлекторные) двигатели (БКД). Такие электромеханические преобразователи состоят из синхронного двигателя, с ротором которого связан датчик положения ротора. Этот датчик обеспечивает коммутацию обмоток управления, расположенный на статоре электрической машины. На ее роторе располагаются постоянные магниты. Функциональная схема такого электромеханического преобразователя представлена на рис. 4.

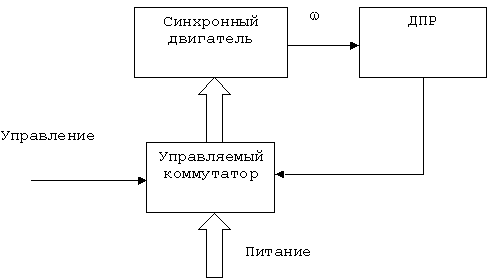
Рис. 4. Функциональная схема БКД.

Момент, развиваемый БКД определяется как:

,

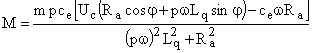где 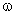— угловая скорость вала,

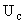– напряжение управления двигателем,

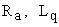– сопротивление и индуктивность фазной обмотки двигателя,

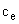– коэффициент пропорциональности между напряжением на фазных обмотках двигателя и угловой скоростью его вала,

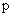– число пар полюсов двигателя,

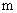– число фаз обмотки управления,

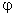— угол сдвига между основной гармоникой ЭДС фазы и фазовым напряжением.

При малой индуктивности фазных обмоток двигателя и величине угла сдвига между основной гармоники ЭДС и фазовым напряжением, близким к 90 градусов, величина момента, развиваемого БКД, определяется как

.

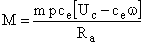Таким образом, вид механической характеристики БКД достаточно близок к аналогичным характеристикам двигателя постоянного тока. Поэтому, для исследования САУ, содержащих бесконтактные двигатели, используются передаточные функции, полученные для двигателей постоянного тока.

Механические системы.

Механизмы передачи крутящих моментов широко используются для согласования скоростей рабочих машин или исполнительных механизмов и приводных двигателей. Среди них наибольшее распространение находят зубчатые передачи.

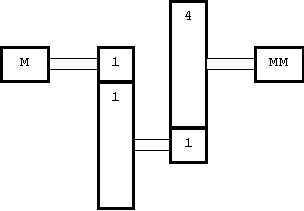
Рис. 5. Пример простейшей кинематической передачи.

Динамические процессы, происходящие в большинстве механизмов, неразрывно связаны со свойствами входящих в него механических систем. Особенности получения динамических моделей механизмов с линейными функциями положения и линейными характеристиками упругих звеньев можно рассмотреть на примере механической системы, представленной на рис. 5. Здесь ротор двигателя М и вращающееся исполнительное звено MM связаны передаточным механизмом, состоящим из зубчатых колес 1-4, образующих двухступенчатый редуктор. 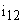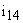Пусть передаточное отношение первой пары — , а – общее передаточное число редуктора. Моменты инерции всех звеньев относительно их собственных осей – .

При составлении динамической модели механизма будем учитывать крутильные податливости соединительных валов и зубчатых передач. При этом под податливостью понимается величина, обратная жесткости вала с, которая определяется как

,

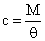где 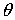— угол закручивания элемента механизма.

Вычисление податливости валов, связывающих элементы рассматриваемого механизма, подробно описано в литературе по теоретической и прикладной механике. Для вычисления жесткости зубчатой передачи со стальными зубьями можно пользоваться эмпирической зависимостью:

,

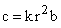где 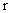– радиус ведущего колеса, см; 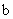– ширина зубчатого венца, см; .

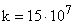Обозначим жесткости зубчатых передач 1-2 и 3-4 как 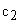и 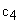соответственно. Жесткости валов, связывающих элементы механизма, обозначим как 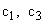и 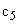. В большинстве своем упругие элементы передаточного механизма обладают диссипативными свойствами, то есть способностью рассеивать механическую энергию. В общем случае зависимость силы сопротивления от скорости может быть достаточно сложной функцией. Коэффициент, характеризующий диссипативные свойства, может быть непостоянным, а показатель степени, в которую возводится величина скорости, отличен от единицы. Решение таких задач выходит за рамки настоящего пособия. Будем рассматривать механические системы, в которых присутствуют силы вязкого трения, пропорциональные скорости движения элементов механизма. Эти силы характеризуются коэффициентами демпфирования 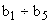. Иными словами, полагаем, что при изменении деформации 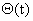элемента механизма с номером r возникает момент, определяемый как

.

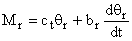Рассматриваемая система имеет шесть степеней свободы. В качестве обобщенных координат удобно принять углы поворота ротора двигателя и зубчатых колес, приведенные к ротору двигателя. То есть

, , ,

, , .

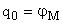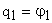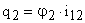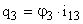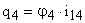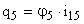При этом деформации валов и зубчатых колес, приведенные к валу двигателя, определяются как

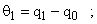
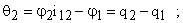
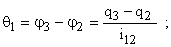
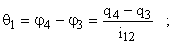
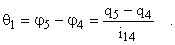
Из уравнения Лагранжа следует, что система дифференциальных уравнений, описывающая движение отдельных элементов механизма, может быть представлена в следующем виде

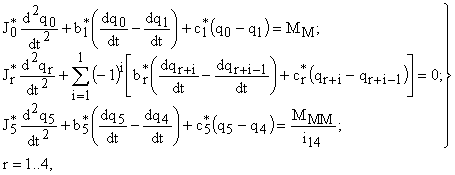(7)

где 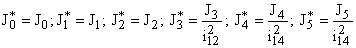– моменты инерции звеньев, приведенные к валу двигателя,

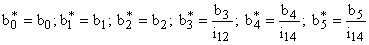— значения коэффициентов демпфирования, приведенные к валу двигателя,

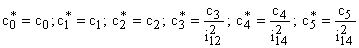— значения жесткости элементов кинематической цепи, приведенные к валу двигателя, 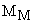– момент, развиваемый приводным двигателем,

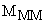– момент сопротивления рабочей машины.

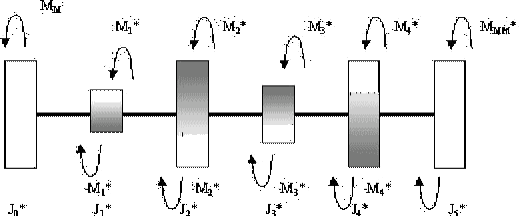
Рис. 6. Цепная динамическая модель механизма.

На рис. 6 представлена цепная динамическая модель механизма, для которой уравнения вынужденных колебаний, вызываемых активными приложенными силами и моментами инерции, совпадают с движениями, возникающими в системе, представленной выражением (7).

На рисунке 6 принято, что величина динамического момента 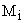определяется как

.

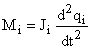Таким образом, динамические ошибки, вызванные податливостью звеньев, могут рассматриваться как вынужденные крутильные колебания многомассовой системы вблизи траектории программного движения механизма с абсолютно жесткими звеньями.

Система уравнений (7) в операторной форме записывается как

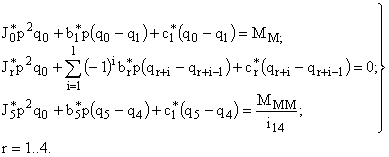(8)

Из системы (8) определяются передаточные функции, связывающие законы изменения обобщенных координат с законами изменения обобщенных сил. Соответствующие им частотные характеристики имеют размерность податливости. Кроме того, возможно получение передаточных функций, связывающих величины обобщенных сил с моментами, прикладываемыми к редуктору со стороны двигателя и исполнительного механизма. Такие характеристики позволяют определить величины динамических моментов, возникающих в различных элементах механизма при разных режимах его работы.

Так как основные параметры зубчатых передач определяются исходя из требуемой нагрузочной способности, то в подавляющем большинстве случаев податливости спроектированных зубчатых колес значительно меньше податливостей элементов их соединения с рабочей машиной и приводным двигателем. Поэтому с достаточной степенью точности можно утверждать, что жесткости зубчатых колес общепромышленных механизмов бесконечно велики. Исходя из этого эвристического положения, двухступенчатый редуктор можно рассматривать как трехмассовую систему, параметры которой определяются следующим образом:

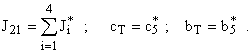
Структурная схема такого представления двухступенчатого редуктора показана на рис. 7.

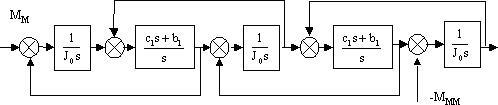
Рис. 7. Структурная схема механизма с двухступенчатым редуктором

На рис.8 изображены логарифмическая (а) и амплитудно-фазовая (б) частотные характеристики такого механизма.

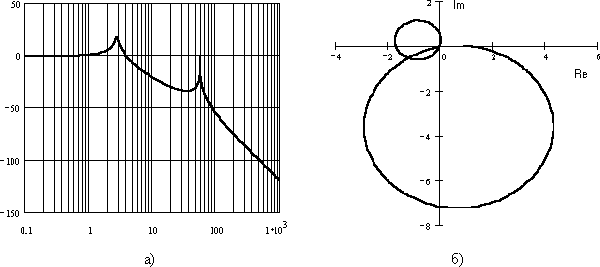
Рис. 8. Частотные характеристики двухступенчатого редуктора (а – логарифмическая, б — амплитудно-фазовая)

Лекция 9