Шаг интегрирования - это
1)расстояние между узлами интерполяции
2)расстояние между значениями аргументов
3)разность между значениями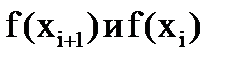 
4)в списке нет правильного ответа
3. Шаг равномерной сетки изменения х на отрезке [a;b] вычисляется по формуле (n – число узлов)
1) 
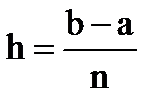
2) 
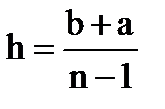
3) 
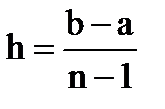
При решении задачи численного интегрирования интерполяция используется
1)на этапе вычисления элементарного интеграла
2)при вычислении конечных разностей
3)при вычислении шага интегрирования
4)в списке нет правильного ответа
Погрешность интегрирования при уменьшении числа разбиений
1)уменьшится
2)увеличится
3)останется без изменений
4)в списке нет правильного ответа
В методе прямоугольников подынтегральная функция заменяется интерполяционным многочленом
1)1-й степени
2)2-й степени
3)0-й степени
4)в списке нет правильного ответа
В методе трапеций подынтегральная функция заменяется интерполяционным многочленом
1)1-й степени
2)2-й степени
3)3-й степени
Метод численного интегрирования, в котором подынтегральная функция заменяется полиномом нулевой степени, называется
1)методом трапеций
2)методом прямоугольников
3)методом Симпсона
4)методом Гаусса
Количество интервалов разбиения, кратное двум, необходимо выбирать для вычисления интеграла
1)методом трапеций
2)методом левых прямоугольников
3)методом Симпсона
4)методом средних прямоугольников
Меньшее количество интервалов разбиения при вычислении интеграла с заданной точностью потребуется для
1)метода трапеций
2)метода правых прямоугольников
3)метода средних прямоугольников
4)метода Симпсона
Обеспечить вычисление интеграла с заданной точностью можно, используя
1)метод двойного просчета
2)метод автоматического выбора шага
3)метод Рунге-Кутта
4)метод Симпсона
Элементарный отрезок интегрирования в методе Симпсона равен
1)одному шагу интегрирования
2)двум шагам интегрирования
3)трем шагам интегрирования
4)четырем шагам интегрирования
В методе Симпсона количество интервалов разбиения должно быть
1)не менее пяти
2)кратным трем
3)кратным двум
4)кратным четырем
14. В формуле правила Рунге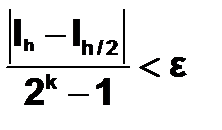 
значение коэффициента k в методах Симпсона, левых и правых прямоугольников и трапеций, равны соответственно
1)3, 1, 2
2)1, 2, 3
3)2, 3, 1
4)4, 1 , 2
Пара методов, обеспечивающих точность одного порядка это
1)метод трапеций и метод средних прямоугольников
2)метод правых прямоугольников и метод Симпсона
3)метод левых прямоугольников и метод трапеций
Значение интеграла, вычисленное с использованием формулы трапеции, для функции, заданной таблично, равно
| x | 0.1 | 0.2 | 0.3 | 0.4 |
| y(x) | -4 | -3.8 |
1)0.48
2)-0.48
3)0.83
4)0.38