Основные этапы математического моделирования

Моделирование ХТС состоит из нескольких этапов.

Первый этап уже был собственно рассмотрен.В целом первый этап связан с формулировкой (постановкой) задачи. На этом этапе задача осмысливается, как правило, с физической точки зрения. Здесь определяются конечные цели исследования и строится каноническая модель. Построение модели начинают с разработки концептуальной модели (концепция-система взглядов на что-то). На этом этапе определяются направление, цели и область исследования. Обычно построение концептуальной модели начинается с постановки проблемы, которая есть у заказчика. Как правило, описание проблемы дается в весьма нечетких формулировках (иначе бы заказчик сам решил, что надо делать). На основании этого исследователь должен определить задачу исследования. Совместная работа заказчика и исполнителя позволяет сформулировать цель и задачу исследования ХТС и создать сценарий функционирования системы.

Для построения сценария выполняется довольно значительный объем работы, связанный с обследованием объекта и составлением сценария, в котором в словесном или графическом виде концентрируются все сведения об объекте: его природа, назначение, структура, взаимодействие отдельных элементов и т.д.

Определяются факторы, влияющие на объект и на окружение. Формулируются цели, стоящие перед объектом и определяется критерий оптимальности. Особо выделяются управляемые факторы. На заключительном этапе построения концептуальной модели проверяется ее адекватность (соответствие) реальной системе.

Второй этап - построение математической модели или математическая формулировка задачи. Для построения математической модели используются основные законы химии, физики и др. наук. Математическая модель любого технологического процесса состоит собственно из уравнений, описывающих данный процесс, начальных и граничных условий и ограничений, записанных в виде равенств или неравенств. Второй этап наиболее трудоемкий и ответственный. Качество математической модели зависит от степени изученности процесса.

Третий этап- выбор численного метода. Как правило, инженер использует для решения программы наиболее целесообразный численный метод решения задачи.

Четвертый этап - разработка алгоритма и построение блок-схемы. Алгоритм - это последовательность элементарных арифметических и логических операций, приводящих к конечному результату.

Блок-схема - это графическое изображение алгоритма.

Пятый этап - этап программирования. На этом этапе алгоритм задачи записывается на выбранном алгоритмическом языке в виде программы. Особое внимание необходимо уделить выбору алгоритмического языка. Язык не обязательно должен быть бейсиком. Для решения научных задач лучше использовать Фортран или Паскаль, для экономических задач - алгоритмический язык - Кобол. Для целей управления программу лучше записать на одном из языков Ассемблера.

Шестой этап - отладка программы. Это поиск и исправление ошибок, допущенных при составлении программы. Отлаженная программа многократно проверяется при решении контрольных задач.

Седьмой этап - проведение расчетов. На этом этапе готовятся исходные данные и проводится непосредственно решение самой задачи.

Восьмой этап - обсуждение результатов. Сравнение полученных результатов по модели с экспериментальными данными, полученными из опыта.

Если имеется существенное расхождение между рассчитанными по модели значениями и экспериментальными данными, то обычно возвращаются к первому этапу и модель усложняют. Если разница несущественная, то пишется отчет о проделанной работе и модель начинают использовать в производстве.

Два подхода к описанию ХТС

На сегодня имеется два подхода к математическому описанию ХТС:

Первый подход называется структурным. В этом подходе для создания математической модели исследуется структура ХТС. Структуру ХТС образуют отдельные элементы ХТС и связи между ними. Например, применительно к синтезу это означает расшифровку его механизма и создание мысленной модели синтеза. Применительно к химическому процессу, протекающему в аппарате, это означает не только расшифровку механизма синтеза, но и учет движения потоков среды (он может быть ламинарным или турбулентным), учет процесса переноса тепла и массы.

После создания мысленной модели ее записывают на языке математики в виде уравнений в самом общем виде. Эти уравнения и есть собственно модель процесса. Если процесс протекает в аппарате определенного типа общую математическую модель уточняют, т.е. коэффициенты (параметры) модели заменяют на числовые значения, которые определяют на промышленном аппарате. Структурный подход требует длительных кропотливых исследований. Его основное достоинство - большая прогностическая мощность, т.е. полученную модель можно использовать для масштабирования.

В случае структурного подхода математическое описание ХТС представляет в общем случае систему уравнений вида

Y_i = F_i (X,H,Z)

где Х контролируемые и регулируемые параметры; Н - контролируемые, но не регулируемые входы; Z - неконтролируемые и нерегулируемые входы.

Это зависимости выходных параметров от входных. Однако установить вид функции F принципиально невозможно, т.к. неизвестны параметры Z .

Поэтому математическое описание системы представляют в виде:

Y_i = F_i1 (X,H) + F_i2 (Z)

Здесь функции F_i разбиты на две функции: первая зависит только от контролируемых факторов, вторая функция определяет шум или оценку шума системы. Задача сводится к определению вида функции F₁ оценке шума F₂.

Очень часто под математической моделью системы понимают модель:

Y_i = F_i1 (X,H)

Это неполная математическая модель ХТС.

Второй подход называется эмпирическим или методом черного ящика. В этом подходе принципиально отказываются от изучения структуры ХТС. (Эмпиризм - это философское направление, признающее чувственное восприятие и опыт единственным источником познания. Эмпиризм не допускает никакого обобщения).

Под черным ящиком понимается такая система о внутренней структуре которой ничего не известно. Любую ХТС можно изобразить в виде черного ящика:

	Внешняя среда

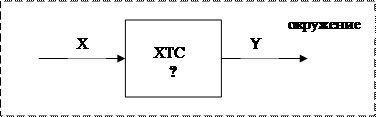Смысл второго подхода заключается в изучении поведения системы в зависимости от воздействия управляемых и контролируемых факторов, т.е. в установлении математических зависимостей:

Y_i = F_i1 (X,H)

Главное достоинство эмпирического подхода это его относительная простота. Чем сложнее система, тем эффективней эмпирический подход.

Основной недостаток - малая прогностическая мощность. Полученные математические модели нельзя использовать для целей прогнозирования и масштабирования вне изученных пределов изменения входных параметров.

При эмпирическом подходе в качестве математической модели используют чаще всего полином какой то степени, например, полином первой степени для трех переменных имеет вид:

Y= b₀+b₁ X₁+ b₂ X₂ +b₃ X₃

Математические свойства полиномов хорошо изучены. Поэтому такие модели широко используются для описания ХТС.

В планировании эксперимента для построения математических моделей используется второй подход.

Поскольку такие модели являются наиболее простыми, то лучше изучать построение моделей именно с них. Но для этого надо знать теорию вероятностей и математическую статистику. Теория вероятностей - это наука, изучающая закономерности в случайных явлениях.

Таким образом, такие модели используются только для интерполяции, т.е. предсказания свойств внутри изученной области изменения переменных.

При разработке моделей всегда используются в той или иной степени элементы эмпирического и структурного подхода. В структурном подходе на завершающей стадии всегда используются элементы эмпирического подхода. Таким образом, эти два метода взаимно дополняют друг друга.