V. Продолжение работы по теме урока. 1. В ы п о л н е н и е задания № 407

1. В ы п о л н е н и е задания № 407.

– Как называются данные фигуры? (Пирамида и призма.)

– Что вы знаете о данных фигурах? Что их объединяет? (Это объемные тела.)

С п р а в о ч н ы й м а т е р и а л д л я у ч и т е л я

Призмой называется многогранник, который состоит из двух плоских многоугольников, совмещаемых параллельным перекосом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (рис. 1). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, – боковыми ребрами призмы.

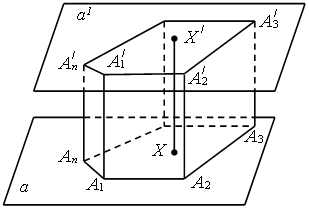
Рис. 1

Так как параллельный перекос есть движение, то основания призмы равны. Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у призмы основания лежат в параллельных плоскостях. Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у призмы боковые ребра параллельны и равны.

Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. У каждого из этих параллелограммов две стороны являются соответствующими сторонами оснований, а две другие – соседними боковыми ребрами.

Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы.

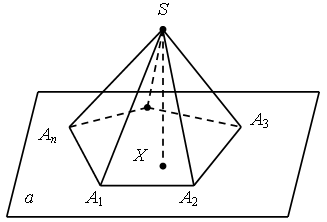
Рис. 2

Диагональным сечением призмы называется сечение плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани. Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.

Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды и всех отрезков, соединяющих вершину с точками основания (рис. 2). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Пирамида называется п-угольной, если ее основанием является п-угольник. Треугольная пирамида называется также тетраэдром.

– Сравните данные фигуры и назовите как можно больше признаков сходства между ними. (Равные высоты, в основании – шестиугольник, одинаковое количество граней.)

– Выделите как можно больше различий между фигурами. (У пирамиды есть вершина и одно основание.)

– Как можно изменить одну из фигур так, чтобы количество различий между ними увеличилось? (Изменить высоту; изменить размеры основания; изменить многоугольник, который лежит в основании.)

2. Р а б о т а в печатной тетради № 3, задание № 60.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие фигуры называют пирамидой и призмой?

– Когда дробь равна 1? Больше? Меньше 1?

Домашнее задание:тетрадь № 3, задание № 59.

У р о к 121 (41).
Решение задач на движение

Цели: рассмотреть задачу на движение, имеющую несколько решений; учить изменять условие задачи так, чтобы решение было единственным; продолжить работу по составлению краткой записи и решению составных задач по действиям и выражениям, преобразованию условия после решения; развивать умения выбирать удобный единичный отрезок и отмечать на координатном луче точки, соответствующие различным дробным числам; развивать умение анализировать и обобщать.

Ход урока