V. Продолжение работы по теме урока. 1. Ф р о н т а л ь н а я р а б о т а

1. Ф р о н т а л ь н а я р а б о т а.

З а п и с ь на доске:

– Разделите данные выражения на две группы. Какой признак вы использовали? (I группа – все суммы; II группа – разности.)

– К каждой выделенной группе запишите 3 своих выражения.

– Найдите значения выражений.

– Какие знания вы использовали?

– Сравните значения всех выражений. На какие три группы можно разделить данные выражения? Укажите признак каждой группы.

(I группа – выражения, значения которых меньше 1, то есть числитель меньше знаменателя (правильные дроби);

II группа – выражения, значения которых равны 1, то есть числитель равен знаменателю;

III группа – выражения, значения которых больше 1, то есть числитель больше знаменателя (неправильные дроби).)

– К каждой группе запишите несколько соответствующих ей выражений и найдите их значения.

2. П о с т р о е н и е т р е у г о л ь н и к а в тетради.

– Что изображено на доске? (Отрезок и два угла.)

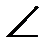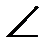– Выполните измерения, постройте треугольник с данными углами и стороной. (а = 4 см, 50°, 45°.)

– Какая фигура называется треугольником? Что вы знаете об этой фигуре?

С п р а в о ч н ы й м а т е р и а л д л я у ч и т е л я

Треугольником называется фигура, которая состоит из трех точек», не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – его сторонами. На рис. 1 вы видите треугольник с вершинами А, В, С и сторонами АВ, ВС, АС. Треугольник обозначается указанием его вершин. Вместо слова «треугольник» иногда употребляют значок D. Например, треугольник на рисунке 16 обозначается так: D АВС.

Углом треугольника ABC при вершине А называется угол, образованный полупрямыми АВ и АС. Так же определяются углы треугольника при вершинах В и С.

Рис. 1

– Как могут располагаться углы треугольника относительно данной стороны?

– Сколько решений у вас получилось?

– Сравните свои треугольники с решениями в пункте 3.

3. Р а б о т а в печатной тетради № 3, задание № 58.

– Что такое координатный луч?

– Что называют координатой?

– Что такое единичный отрезок?

– От чего зависит выбор единичного отрезка на числовом луче?

– Чему равен единичный отрезок на данном числовом луче?

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить сложение и вычитание дробей с равными знаменателями?

– Какую фигуру называют треугольником?

Домашнее задание:учебник, № 396 (3); тетрадь № 3, задание № 57.

У р о к 120 (40).
Сравнение дробей с единицей. Дроби,
меньшие единицы. Дроби, большие единицы.
Дроби, равные единице. Соотношение числителя
и знаменателя таких дробей

Цели: провести сравнение дробей и выявить признаки дробей, равных 1, больших 1 и меньших 1; учить записывать дроби согласно данному условию; совершенствовать умения выполнять действия сложения и вычитания с дробными числами; учить составлять сложные выражения с дробными; продолжать работу по сравнению пространственных фигур, научить выделять признаки, сходство и различие пирамиды и призмы; развивать логическое и пространственное мышление.

Ход урока