IV. Работа по теме урока. 1. В ы п о л н е н и е задания по теме урока
1. В ы п о л н е н и е задания по теме урока.
– Прочитайте данные числа.
– Чем они похожи? Чем отличаются?
– Продолжите ряд чисел.
– На сколько каждое следующее число ряда больше предыдущего? (На десять тысяч.)
– Какое число будет стоять в ряду на десятом месте? Запишите и прочитайте это число.
| 100 000 – сто тысяч |
В шестизначном числе появляется еще один разряд – сотни тысяч.
Посчитайте новой единицей счета и запишите цифрами получившиеся числа.
Проверьте свою запись по пункту 5.
Подчеркните в своей записи числа, данные в пункте 6.
2. Р е ш е н и е задачи (см. условие на с. 280 данного пособия, п. 2).
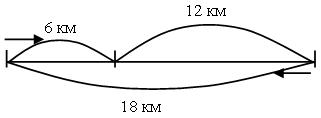
На сколько километров должно отнести течением на север льды, чтобы к концу дня путешественник оказался там же, откуда он начал двигаться? (На 18 км.)
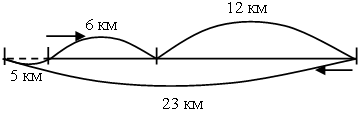
– На сколько километров отнесло течением на север льды, если к концу дня путешественник оказался на 5 км севернее точки отправления? (На 23 км.)
 Ф и з к у л ь т м и н у т к а
Ф и з к у л ь т м и н у т к а
V. Продолжение работы по теме урока.
1. В ы п о л н е н и е задания № 429.
– Как называется математическая запись в пункте 1? (Уравнение.)
– Сколько действий необходимо выполнить, чтобы решить это уравнение?
– Предложите свой способ решения этого уравнения.
у : 9 + 637 = 745
у : 9 = 745 – 637
у : 9 = 108
у = 108 ∙ 9
у = 972
– Проверьте свое решение с рассуждениями в пункте 3.
2. Ф р о н т а л ь н а я р а б о т а.
| – Какое объемное тело называют призмой? – Какая призма изображена на доске? – Как определить площадь поверхности призмы? (Можно использовать развертку призмы.) | 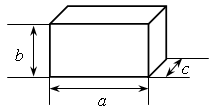 |
а = 4 см
b = 2 см
c = 3 см
| S осн = 4 ∙ 3 = 12 (см2) S бок. р = 2 ∙ 3 = 6 (см2) S пер. р = 4 ∙ 2 = 8 (см2) | Sповерх = 12 ∙ 2 + 6 ∙ 2 + 8 ∙ 2 = 52 (см2) |
– Как изменится площадь поверхности призмы, если одно ее измерение увеличить на 2 см?
| а = 4 см b = 3 см с = (2 + 2) см Р е ш е н и е: S = (12 + 12 + 16) ∙ 2 = 80 см2 | а = 4 см b = (3 + 2) см с = 2 см Р е ш е н и е: S = (20 + 10 + 8) ∙ 2 = 76 см2 |
а = (4 + 2) см
b = 3 см
с = 2 см
Р е ш е н и е:
S = (18 + 6 + 12) ∙ 2 = 72 см2
(При изменении длины, ширины или высоты прямоугольной призмы на 2 см значение площади поверхности призмы будет различным.)
– Какую зависимость вы заметили при увеличении на 2 см? (72 см2, 76 см2, 80 см2.)
– Как изменится площадь поверхности призмы, если одно ее измерение увеличилось в 2 раза?
| а = 4 см b = 3 см с = (2 ∙ 2) см Р е ш е н и е: S = (12 + 16 + 12) ∙ 2 = 80 см2 | а = 4 см b = (3 ∙ 2) см с = 2 см Р е ш е н и е: S = (20 + 8 + 10) ∙ 2 = 76 см2 |
а = (4 ∙ 2) см
b = 3 см
с = 2 см
Р е ш е н и е:
S = (24 + 16 + 6) ∙ 2 = 92 см2
– Зависит ли изменение площади поверхности призмы от выбора измерения для увеличения в 2 раза?
3. Р а б о т а в печатной тетради № 3, з а д а н и е № 82.
П р и м е ч а н и е. Продолжение и усложнение задания 77. Оно требует более серьезных размышлений, так как цепочки имеют 2 общих звена, в которые попадут цифры 8 и 3. Всего задание имеет 4 решения, но каждый ученик имеет право ограничиваться только двумя. Все найденные решения нужно обсудить.
Цифра 6, тоже встречающаяся в обоих числах, не может стоять в общем звене, так как она не стоит рядом ни с 3, ни с 8.
VI. Итог урока.
– Что нового вы узнали на уроке?
– Назовите наивысший разряд шестизначного числа.
– Как вычислить площадь поверхности призмы?
– Что такое развертка объемного тела?
Домашнее задание: тетрадь № 3, задание № 84.
У р о к 138 (58).
Образование сотни тысяч различными способами
Цели: рассмотреть все пять способов образования сотни тысяч; провести сравнение названий сотен и сотен тысяч; развивать умения записывать числа согласно предложенному условию; вести наблюдения за местом, которое занимает новая единица счета в записи числа; продолжить работу по заполнению промежутков между полученными опорными числами; закреплять умения решать составные задачи, в которых требуется нахождение части числа; совершенствовать умения составлять обратные задачи; закреплять умения выполнять преобразования величин; продолжить формирование умений выполнять сложение многозначных чисел и выделять заранее приготовленную закономерность в расположении сумм; развивать умение анализировать и рассуждать.
Ход урока
