V. Продолжение работы по теме урока. 1. Ф р о н т а л ь н а я р а б о т а
1. Ф р о н т а л ь н а я р а б о т а.
– Прочитайте условие задачи: «В аквариуме поселили 25 рыбок – гуппи и меченосцев. Гуппи в нем на 7 больше, чем меченосцев. Сколько в аквариуме рыбок каждого вида?».
– Что известно в задаче? Что требуется узнать?
– Как лучше оформить краткую запись задачи?
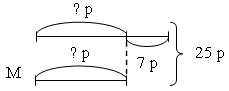
Р е ш е н и е:
1) 25 – 7 = 18 (р.) – столько рыбок было, если бы гуппи было столько же, сколько меченосцев.
2) 18 : 2 = 9 (р.) – было меченосцев.
3) 25 – 9 = 16 (р.) – гуппи.
Или:
9 + 7 = 16 (р.) – было гуппи.
О т в е т: 16 меченосцев, 9 гуппи.
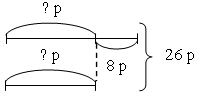
– Замените в задаче число 7 числом 8 и решите новую задачу.
1) 25 – 8 = 17 (р.) – меченосцев и гуппи поровну.
2) 17 : 2 – невозможно.
– Какие изменения нужно внести в условие задачи, чтобы ее решение стало возможным? (Искомые числа – общее число рыбок и разница между количеством меченосцев и гуппи – должны быть или четными, или нечетными числами.)
2. В ы п о л н е н и е задания № 319.
– Что объединяет данные записи?
– Что такое уравнение?
– Что значит найти корни уравнений?
– Найдите и решите уравнения, запись которых соответствует договоренности, с которой вы познакомились в задании № 311.
| 6 y = 936 y = 936 : 6 y = 156 | 8 t = 464 t = 464 : 8 t = 508 |
– Какие знания помогли вам выполнить это задание?
– Какие уравнения можно записать аналогично решенным? Запишите их и решите.
| 7 b = 938 b = 938 : 7 b = 134 | 3 а = 813 а = 813 : 3 а = 271 |
3. Р а б о т а в печатной тетради № 3, задание № 9.
Р е ш е н и е. Верно изображен цилиндр на втором и четвертом чертежах.
– Какие объемные тела называют цилиндром?
– Какие условные обозначения используют на чертеже?
VI. Итог урока.
– Что нового узнали на уроке?
– Что называют числовым лучом?
– Что такое единичный отрезок?
– Какие знания необходимы для решения уравнений?
Домашнее задание: учебник, № 331; тетрадь № 3, задание № 9.
У р о к 97 (17).
Высота пирамиды
Цели: познакомить с оксонометрической проекцией пирамиды; ввести понятие высоты пирамиды, учить делать чертеж пирамиды; продолжать работу по сравнению разной формулировки одной и той же задачи, отрабатывать навык составления и решения обратных задач; закреплять умения восстанавливать сложное выражение по выполненным действиям; совершенствовать вычислительные навыки при решении сложных выражений на порядок действий; развивать умение анализировать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
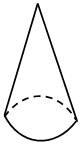
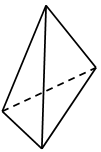
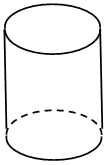
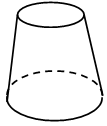
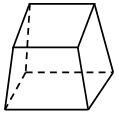
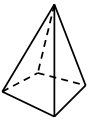
1. Д о г а д а й с я! По какому признаку можно разбить фигуры на группы?
 |  |  |  | |||
 |  |  | ||||
О т в е т ы д е т е й.
а) – Я разобью на две группы. Первая группа – это фигуры 1, 3, 4. Вторая – 2, 5, 6, 7.
б) – А у меня получилось три группы. Первая – 1, 2, 6. Вторая – 3, 4. Третья – 5, 7.
– Объясните, как вы рассуждали.
2. И г р а «Угадай задуманное число».
Ÿ Задумайте любое однозначное число, кроме нуля.
Ÿ Увеличьте его в 5 раз.
Ÿ Вычтите из результата задуманное число.
Ÿ Полученную разность разделите на задуманное число.
Ÿ Прибавьте к результату 96.
Ÿ Получилось 100.
– Объясните, почему всегда получается 100.
3. О б ъ я с н и т е, в каком порядке должны выполняться действия по схематическим записям, в которых  обозначает число.
обозначает число.
а)  +
+  –
–  +
+  +
+  –
– 
б)  ∙
∙  :
:  ∙
∙  ∙
∙ 
в)  +
+  ∙
∙  –
–  :
:  +
+ 
г)  – (
– (  +
+  ) +
) +  ;
;  – (
– (  +
+  ) +
) +  –
–  )
)
д)  – (
– (  –
–  ∙
∙  ) +
) + 
е)  – (
– (  +
+  :
:  ) ∙
) ∙ 
