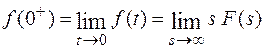По определению преобразование Лапласа

L[k₁ f₁(t) 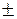k₂ f₂(t)] =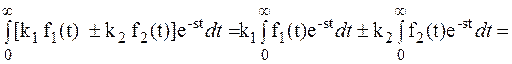

k₁F₁(s) 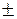k₂ F₂(s).

Замечание.

Из данной теоремы следует, что преобразование Лапласа линейной комбинации оригиналов равно той же линейной комбинации их изображений.

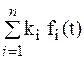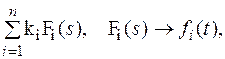
L[ ] = 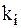- const.

2.Изображение производной.

Теорема 2.

Если функции f(t) и f'(t) функция f(t) имеет изображение F[s], то преобразование Лапласа производной этой функции равно:

L[f(t)] = s F[s] – f(0⁺)

f(0⁺) =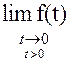

Теорема утверждает, что дифференцирование в вещественной области в комплексной области соответствует операции умножения изображения на s.

Доказательство.

По определению функция F[s] это:

F[s] =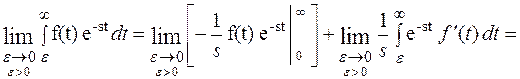

] =

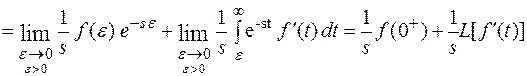
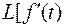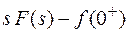
Покажем, что

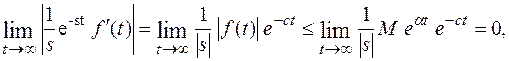при с > α.

Последовательное применение теоремы 2 позволяет распространить ее на производную любого порядка.

] =

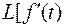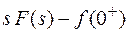
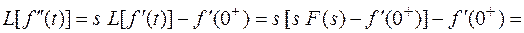
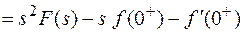
Продолжая процесс, можно установить, что для n-ой производной:

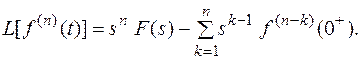
3.Изображение интеграла.

Теорема 3.

Если функция f(t)-оригинал и имеет изображение F[s], то интеграл

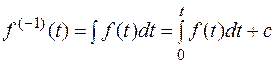
также является оригиналом, причем

L[ 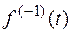] = F(s)/s +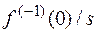

L[ 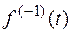] = F(s)/s + 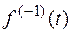/s.

Теорема утверждает, что интегрирование в вещественной области в комплексной области соответствует делению изображения на s (с точностью до const).

Доказательство. (2-ой части, которая приводит к формуле задания изображения).

По определению

F(s) =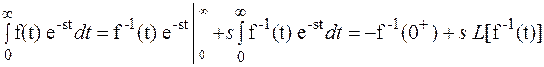

L[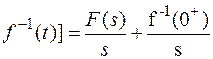

Покажем, что

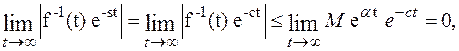при .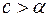

Теорема доказана.

4.Изменение масштаба.

Теорема 4.

Если функция f(t) оригинал и имеет изображение F(s), и «a» - некоторая положительная константа или положительная переменная независящая от t и s, то преобразование Лапласа:

L =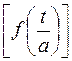

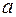
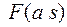
График функции 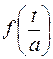отличается от графика функции f(t) наличием масштаба по оси t.

Доказательство.

По определению

F(W) =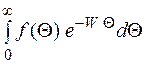

Положи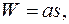м, имеем

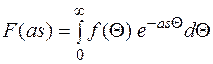
Введем 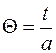, тогда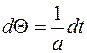

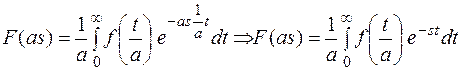
L = .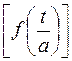

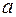
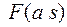Пример.

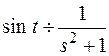
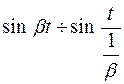
В соответствии с теоремой 4.

.

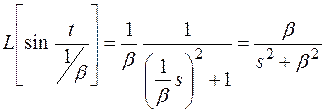5.Смещение в комплексной области.

Теорема 5.

Если функция f(t) оригинал и имеет изображение F(s), то

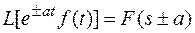
Доказательство.

По определению преобразование Лапласа

.

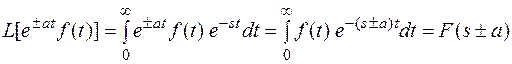
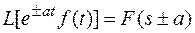Пример 1.

Найти преобразование Лапласа.

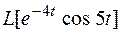
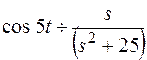
по теореме 5

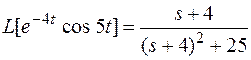
Пример 2.

Найти обратное преобразование Лапласа.

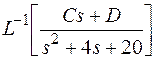
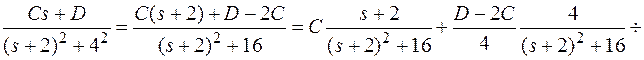
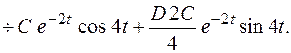
6. Теорема свертки.

Сверткой функции f₁(t) и f₂(t) называется функция

f(t) =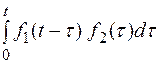

Операция свертки обладает коммутативностью, т. е.

=

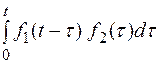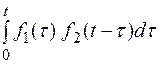
Действительно,

=

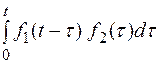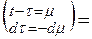
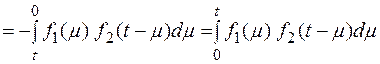
ЛЕКЦИЯ 13

План лекции

1. Свертка функций. Теорема об изображении свертки функций.

2. Изображение запаздывающей функции.

3. Изображение 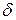-функции и ее производных.

4. Дифференцирование в комплексной области.

Теорема 6.

Если функции f₁(t) и f₂(t) являются оригиналами и имеют соответственно изображения F₁(s) и F₂(s), то

L[ 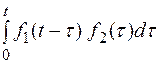] = F₁(s)∙ F₂(s)

Теорема утверждает, что произведению изображений в вещественной области соответствует интеграл свертки.

Доказательство.

Обозначим F(s) = L[ ]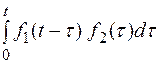

По определению

F(s) =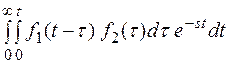

Верхний предел во внутреннем интеграле можно перенести из т. t в т. ∞, если подынтегральное выражение умножить на 1( ).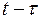

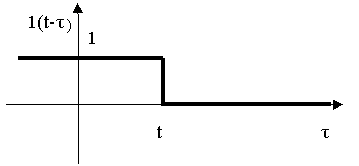
Рис. 1.

F(s) =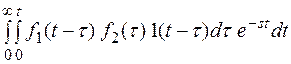

Изменим порядок интегрирования

F(s) =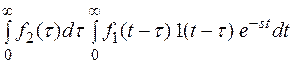

Принимая во внимание вид функции 1(t-τ) как функции аргумента t, запишем

F(s) =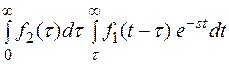

Для второго интеграла введем подстановку 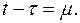Отсюда следует, что

;

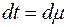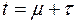
F(s) =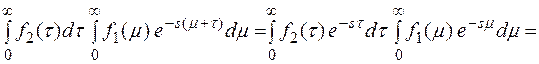

=

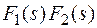
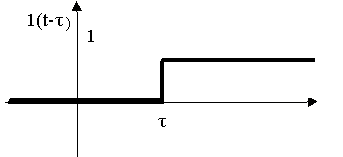
Рис. 2.

Замечание.

Может показаться на первый взгляд, что теорему свертки удобно использовать для вычисления обратного преобразования Лапласа. На самом деле это не так, интеграл свертки приводит к громоздким вычислениям.

7.Изображение запаздывающей функции.

Теорема 7.

Если функция f(t) является оригиналом и имеет изображение F(s), то преобразование Лапласа запаздывающей функции:

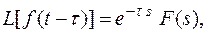при условии

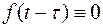при t < τ . (*)

Доказательство.

По определению

F(s) =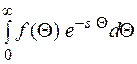

Положим 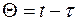, тогда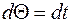

F(s) =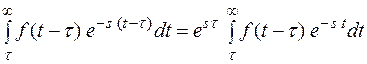

Принимая во внимание соотношение 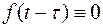при t < τ нижний предел можно перенести из т. τ в т.0. Получим

F(s) = 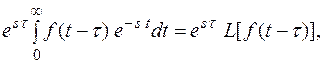отсюда следует, что

.

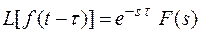Замечание 1.

По условию теоремы функция f(t) является оригиналом, следовательно, может быть записана в виде: f(t)·1(t). Запаздывающий оригинал имеет вид:

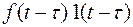, т. е. запаздывающий оригинал обязательно удовлетворяет условию (*).

Замечание 2.

При пользовании данной теоремой во избежание ошибок оригинал следует записывать в виде f(t)·1(t).

Пример 1.

Найти L[ ]

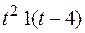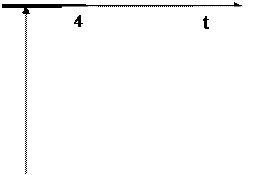По теореме 7 найдем функцию f(t)·1(t)

f(t-4)·1(t-4) = t² 1(t-4) . Очевидно

f(t)·1(t) = (t + 4)² 1(t)

по теореме запаздывания

L[ ] =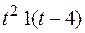

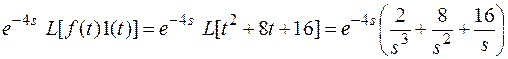
Пример 2.

Найти

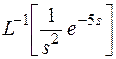
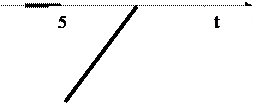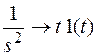
по теореме запаздывания

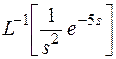= (t – 5) 1(t – 5).

8.Предельный переход по второй независимой переменной.

Теорема 8.

Пусть а – переменная независящая от t и s. Если функция f(t,а) является оригиналом относительно переменной t и имеет изображение F(s,a), то при условии существования выписанных ниже пределов справедливо равенство:

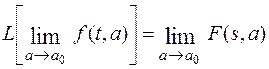
Доказательство.

По определению

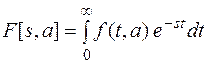
Перейдем к пределу

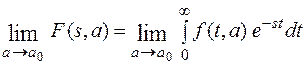
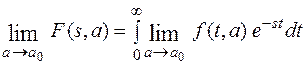
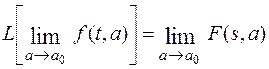
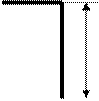
Используя эту теорему, найдем изображение δ - функции. Рассмотрим функцию f(t,a), изображенную на рисунке.

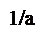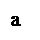Очевидно,

f(t,a) =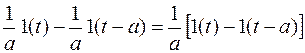

L[f(t,a)] =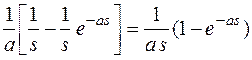

L[f(t- τ)] = 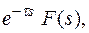где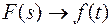

Рассмотрим предел

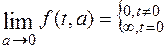
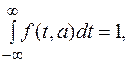т.о.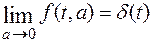

В соответствии с теоремой 8:

L[δ(t)] =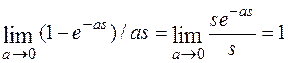

Т. о. Получили L[δ(t)] = 1.

Для производной δ(t) справедливо соотношение

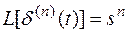
Это равенство формально может быть получено применением теоремы 2.

Для запаздывающей δ(t) справедливо соотношение

L[δ(t-τ)] =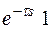

L[ 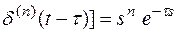(в соответствии с теоремой 7).

9.Дифференцирование в комплексной области.

Теорема 9.

Если функция f(t) является оригиналом и имеет изображение F(s), то

L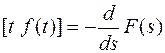

Теорема утверждает, что дифференцирование изображений в вещественной области соответствует умножению оригинала на аргумент t.

Доказательство.

По определению

F(s) =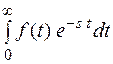

Продифференцируем равенство по s. Это возможно, т. к. F(s)- аналитическая функция в области Re s > .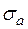

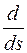F(s) =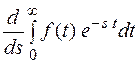

Перейдем к дифференцированию под знаком интеграла, получим

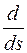F(s) =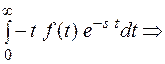 L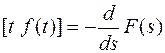

В соответствии с таблицей

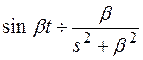
По теореме 9

L[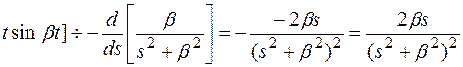

L[

Аналогично

L[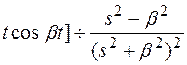

ЛЕКЦИЯ 14

План лекции

1. Теорема о начальном и предельном значениях.

2. Применение преобразования Лапласа для решения дифференциальных уравнений.

3. Обратное преобразование Лапласа рациональной алгебраической дроби.

4. Изображение импульса произвольной формы. Изображение периодических функций.

10.Предельное значение оригинала.

Теорема 10.

Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), и если произведение s F(s) является аналитической функцией в правой полуплоскости на мнимой оси, то

.

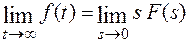Доказательство.

По теореме изображения производной

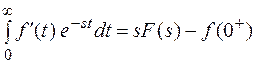
Перейдем пределу при 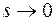, данный предел существует, т. к. функция sF(s) – аналитическая в окрестности 0. Получим

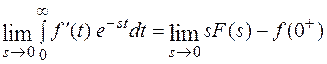
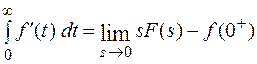
Переход к пределу под знаком интеграла возможен, т. к. по условию теоремы абсцисса абсолютной сходимости для функции 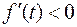, поэтому

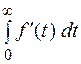- существует.

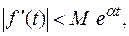наименьшее α - абсцисса абсолютной сходимости.

Re s > 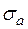, α < 0.

Из равенства

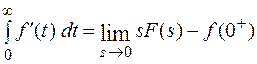следует, что

.

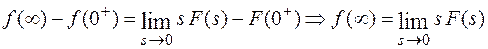Для функции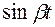

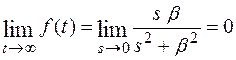
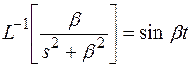
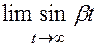- не существует.

Теорема не справедлива, т. к. функция 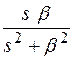имеет два полюса на мнимой оси.

Пример.

Найти 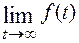, если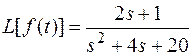

=

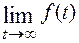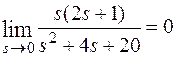
11.Начальное значение оригинала.

Теорема 11.

Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), то

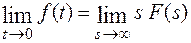
при условии, что 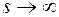т. о., что Re s = c .

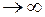Доказательство.

По определению

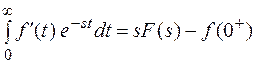
Перейдем к пределу

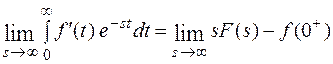
Покажем, что

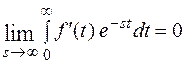
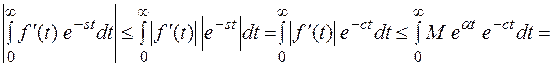
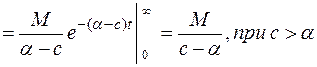
Справедливо равенство

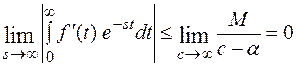
Из равенства

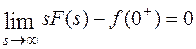
следует, что