Методика изучения избранного алгебраического материала
9.3.1. Методика введения понятия «Одночлен» и формирование умения находить его числовое значение.
К опорным знаниям относятся понятия алгебраического выражения, произведения алгебраических выражений, множителя (числового и буквенного); к умениям – запись алгебраического выражения по его элементам, выделение элементов заданного алгебраического выражения.
Актуализация знаний осуществляется посредством упражнений.
1. Из данного набора выберите такие алгебраические выражения, которые являются произведениями нескольких множителей: а) 5а2b; б) (7аb2 + с2):(5m2n); в) 8; г) 5а6bb4а; д) 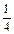 ; е)
; е) 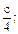 ж)
ж) 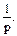
Указанному условию удовлетворяют алгебраические выражения: 5а2b; 8; 5а6bb4а; 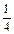 ;
; 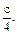 Скорее всего, учащиеся не назовут в числе требуемых алгебраических выражений 8;
Скорее всего, учащиеся не назовут в числе требуемых алгебраических выражений 8; 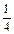 ;
; 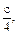 хотя некоторые могут догадаться, что
хотя некоторые могут догадаться, что 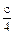 можно представить как
можно представить как 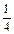 с. Взяв несколько алгебраических выражений, следует поупражняться в выделении их числового множителя, буквенных множителей, в записи по данным алгебраическим выражениям новых выражений.
с. Взяв несколько алгебраических выражений, следует поупражняться в выделении их числового множителя, буквенных множителей, в записи по данным алгебраическим выражениям новых выражений.
2. Составьте новое алгебраическое выражение, используя выражения 3а2b и 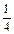 а. Возможные ответы учащихся: 3а2b +
а. Возможные ответы учащихся: 3а2b + 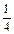 а; 3а2b –
а; 3а2b – 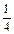 а; 3а2b
а; 3а2b 
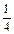 а; 3а2b :
а; 3а2b : 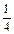 а.
а.
Далее учитель формулирует определение одночлена и предлагает упражнения на распознавание одночленов и выведение следствий из принадлежности данных алгебраических выражений одночленам.
3. Какие из указанных выражений являются одночленами: а) 5а3bсаb4 
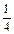 ; б)
; б) 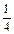 а; в)
а; в) 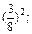 г) 34
г) 34 
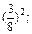 д) 7аb2:n; д) – 5а6
д) 7аb2:n; д) – 5а6 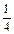 b с2; е) – а3; ж)
b с2; е) – а3; ж) 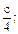 з) – mnx. Назовите числовые и буквенные множители одночленов.
з) – mnx. Назовите числовые и буквенные множители одночленов.
4. Запишите несколько алгебраических выражений, являющихся одночленами.
5. Запишите несколько одночленов, отличающихся только числовым коэффициентом.
6. Заполните пропуски: а) 12а3b4 = 2а…  b2; б) – 24 m2b7p6 = 24bp
b2; б) – 24 m2b7p6 = 24bp  …
…
Далее можно использовать упражнения на запись словесных формулировок в форме алгебраических выражений и обратно.
7. Вместо словесной формулировки записать алгебраические выражения: а) удвоенное произведение чисел а и b; б) утроенное произведение квадрата числа а и числа b.
8. Пояснить выражения: а) 2а  b; б) а
b; б) а  5b.
5b.
Например, выражение а  5b можно пояснить как: 1) произведение чисел а, 5 и b;2) произведение чисел а и 5b;3) площадь прямоугольника со сторонами а и 5b.
5b можно пояснить как: 1) произведение чисел а, 5 и b;2) произведение чисел а и 5b;3) площадь прямоугольника со сторонами а и 5b.
Упражнения типа 7 и 8 способствуют и овладению методом решения текстовых задач с помощью уравнений, так как перевод словесных формулировок на язык чисел и букв и словесная интерпретация алгебраических выражений – важные составляющие метода решения задач с помощью уравнений.
Далее используются упражнения на нахождение числового значения выражения.
9. Найдите числовое значение одночлена: 1) 5mnx при m=3, n= 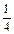 ; x=8; 2) (– 0,25)а
; x=8; 2) (– 0,25)а 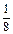 b при а=12; b=8. При выполнении подобных упражнений следует указать особенным учащимся на необходимость использования свойств и законов арифметических действий для рационализации вычислений.
b при а=12; b=8. При выполнении подобных упражнений следует указать особенным учащимся на необходимость использования свойств и законов арифметических действий для рационализации вычислений.
Организация выполнения упражнений может быть различной: решение у доски, самостоятельное решение, комментированное решение, одновременное выполнение упражнений на доске с привлечением слабых учащихся и самостоятельная работа сильных учащихся и т.д.
Для домашнего задания можно использовать упражнения на запись чисел в стандартном виде, которое будет служить мотивом для введения на следующем уроке понятия стандартного вида одночлена.
9.3.2. Обобщение и систематизация знаний по теме: «Прогрессии».
Воспроизведение и коррекцию опорных знаний можно осуществить посредством упражнений на заполнение таблицы с последующим обсуждением результатов.
| Вид прогрессии | Формула общего члена | Зависимость между соседними членами | Сумма первых членов |
| Арифметическая | |||
| Геометрическая |
Отметим, что арифметическая и геометрическая прогрессии дают пример изучения материала в сходных ситуациях, поэтому важное место в систематизации знаний о прогрессиях должны занять методы противопоставления и сопоставления. Обсуждение узловых вопросов основывается на выяснении причин различия и общего в прогрессиях.
Вопросы для обсуждения.
А). Назовите общее и различное в структуре определения арифметической и геометрической прогрессий.
Б). Дайте определение бесконечно убывающей геометрической прогрессии.
В). Что называется суммой бесконечно убывающей геометрической прогрессии? Запишите ее формулу.
Г). Как доказать, что данная последовательность является арифметической (геометрической) прогрессией?
Д). С помощью стрелок покажите связи между указанными определениями, формулами (рис.7):
| a | an = an-1+ d |  | а1, а2, … … | an = al +d(n–1) | |||||
| an, d | |||||||||
an = 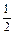 (an-1+ an+1) (an-1+ an+1) | Признак арифметической прогрессии | Sn = 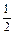 (a1+ a2) n (a1+ a2) n | |||||||
3. Выпишите все определения, формулы по теме «Геометрическая прогрессия» и укажите зависимости между ними.
Упражнения 2 и 3 можно предложить учащимся выполнить самостоятельно с последующим обсуждением результатов всеми учащимися класса. Можно упражнение 2 выполнить коллективно, а упражнение 3 предложить в качестве самостоятельной работы.
Следующие этапы обобщающего урока реализуются с помощью упражнений, выполнение которых требует анализа и использования основных фактов, приводящих к новым связям и отношениям между изученными понятиями и теоремами.
4. Между числами 4 и 9 вставьте положительное число так, чтобы получилось три последовательных члена геометрической прогрессии. Сформулируйте и решите аналогичную задачу применительно к арифметической прогрессии.
5. Определите числа a1, а2, а3 и а4, если a1, а2, а3 – последовательные члены геометрической прогрессии, а a1, а3 и а4 – арифметической прогрессии и а1+ а4= 14, а2 + а3 = 12.
7. Могут ли три положительных числа быть одновременно тремя последовательными членами арифметической и геометрической прогрессий?
8. Можно ли утверждать, что арифметическая и геометрическая прогрессии являются функциями? Если да, то к каким видам функций они относятся?
9. Известно, что an = 2n+1 – арифметическая прогрессия. Что общего и различного в графиках этой прогрессии и линейной функции f(х) = 2x+1?
10. Можно ли указать последовательности, являющиеся
одновременно арифметической и геометрической прогрессиями?
Формы выполнения упражнений могут быть различны: выполнение упражнений у доски, комментированное решение и т.д. Некоторые из приведенных упражнений могут быть выполнены учащимися самостоятельно, причем выполнение их может осуществляться в зависимости от возможностей школьников с применением карточек, содержащих пропущенные строки либо указания к их выполнению. Очевидно, что, чем ниже возможности школьника, тем обширнее для него должен быть набор рекомендаций (указаний к выполнению).
9.3.3. Проверка, оценка и коррекция знаний, умений и навыков по теме: «Умножение и деление рациональных чисел».
Проверка знания учащимися фактического материала, умения объяснять сущность основных понятий осуществляется в процессе беседы с последующим выполнением упражнений.
Вопросы для беседы
1. Сформулируйте правило умножения двух чисел с одинаковыми знаками. Приведите примеры.
2. Сформулируйте правило умножения двух чисел с разными знаками. Приведите примеры.
3. Чему равно произведение нескольких чисел, если одно из них нуль? При каких условиях a  b = 0?
b = 0?
4. Чему равно произведение а  (–1)? Приведите примеры.
(–1)? Приведите примеры.
5. Как изменится произведение при перемене знака одного из множителей?
6. Сформулируйте переместительный закон умножения.
7. Как формулируется сочетательный закон умножения?
8. Запишите, используя буквы, переместительный и сочетательный законы умножения.
9. Как найти произведение трех, четырех рациональных чисел?
10. Ученик, выполняя упражнение на отыскание произведения 0,25  15
15  15
15  (–4), использовал следующую последовательность действий: (0,25
(–4), использовал следующую последовательность действий: (0,25  (–4))
(–4))  15
15  15 = (–1)
15 = (–1)  15
15  15 = –15
15 = –15  15. Какие законы он использовал?
15. Какие законы он использовал?
11. Какой множитель алгебраического выражения называют коэффициентом?
12. Как найти коэффициент произведения, в котором несколько буквенных и числовых множителей?
13. Чему равен коэффициент выражения: a; – a; ab; – ab?
14. Сформулируйте распределительный закон умножения. Запишите его с помощью букв.
15. Какие слагаемые алгебраической суммы называют подобными?
16. Объясните, что значит привести подобные слагаемые.
17. Объясните, с помощью каких законов выполняется приведение подобных слагаемых в выражении 5,2y – 8a – 4,8y – 2а.
18. Каково правило деления рациональных чисел с одинаковыми знаками?
19. По какому правилу выполняют деление рациональных чисел с разными знаками?
20. В каком случае частное двух рациональных чисел равно нулю?
21. В каком порядке выполняют совместные действия с рациональными числами?
Отдельные вопросы могут быть предметом коллективного обсуждения, другие – листов взаимоконтроля учащихся, возможно на основе некоторых вопросов провести математический диктант и т.д.
Последующая серия упражнений направлена на контроль, оценку, коррекцию умений учащихся. Возможны различные формы выполнения упражнений: самостоятельное решение, сопровождающееся самоконтролем учащихся, комментированное решение, выполнение упражнений на доске, устный опрос и т.д. Эта серия охватывает две группы упражнений. Первая группа не требует для выполнения мыслительной деятельности реконструктивного характера, выполнение второй группы предполагает реконструкцию знаний и умений по изучаемой теме.
I группа
1. Какие из указанных равенств верные:
1) (–9)  (–8) = –72; 2) (–1,4)
(–8) = –72; 2) (–1,4)  0,5 = – 0,7;
0,5 = – 0,7;
3) 12  (–0,2) = –0,24; 4) (–3,2)
(–0,2) = –0,24; 4) (–3,2)  (–2,1) = 6,72?
(–2,1) = 6,72?
Выберите правильный ответ.
Ответ: 1); 2); 3); 4); верных равенств нет.
2. Не выполняя вычислений, определите, какое произведение положительно:
1) 0,26  (–17)
(–17)  (–52)
(–52)  (–34); 2) (–1)
(–34); 2) (–1)  (–8)
(–8)  0,4
0,4 
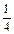
 (–3,4);
(–3,4);
3) (–16)  (–0,87)
(–0,87)  (–
(– 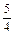 )
)  (–5); 4) 5
(–5); 4) 5  (–3,2)
(–3,2)  0
0  (0,7).
(0,7).
Ответ: 1); 2); 3); 4).
3. Укажите выражения, имеющие равные коэффициенты:
1) 9ас и 3x(4y); 2) (–3)  (–8cb) и 4х
(–8cb) и 4х  6у;
6у;
3) 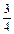 аbс и 2,75xy; 4) 3,15аbс и 0,001аbс.
аbс и 2,75xy; 4) 3,15аbс и 0,001аbс.
4. Какое из выражений содержит подобные слагаемые:
1) 7а – 12аb + 14; 2) – 0,5ху + 2,7kх – 0,5;
3) 3с – 2,7хус – 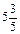 ;4) 72ab –
;4) 72ab – 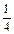 ab + 241?
ab + 241?
Укажите правильный ответ.
Ответ: 1); 2); 4); выражений, содержащих подобные слагаемые, нет.
5. Укажите верные равенства:
1) –3  (11 + 17) = –3
(11 + 17) = –3  11 + 17;
11 + 17;
2) (– 7,6 +14)  (– 7) = – 7,6
(– 7) = – 7,6  (– 7) + 14
(– 7) + 14  (– 7);
(– 7);
3) –1,5  (37–24) = –1,5
(37–24) = –1,5  37–1,5
37–1,5  24.
24.
6. Верно ли выполнено деление:
1) –7,2 : (–9) = 0,8; 2) 48 : (–8) = 6;
3)–5,6:7 = –8; 4) 4,2 : (–1) = – 4,2?
7. Не выполняя вычислений, укажите частное с отрицательным знаком:
1) –7,2 : ((–0,2)  (–12)); 2) (l44
(–12)); 2) (l44 
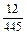 ) : 2,3;
) : 2,3;
3) (14,2  (–0,6)):(–8,49); 4) –2
(–0,6)):(–8,49); 4) –2 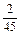 : (–18,2
: (–18,2  100).
100).
Ответ: 1); 2); 3); 4); отрицательных частных нет.
II группа
1. Определите знак выражения:
1) (–0,2)  (–
(– 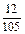 ):16
):16  (–7
(–7 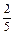 ):0,03
):0,03  (–127);
(–127);
2) 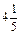 : (– 0,09)
: (– 0,09)  3,25 : (–
3,25 : (– 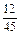 )
)  324 : (– 46,21).
324 : (– 46,21).
2. Упростите выражение:
1) – 5,1  (–3х)
(–3х)  0,2х; 2) – 6,3a(–10bc)
0,2х; 2) – 6,3a(–10bc)  (–8d).
(–8d).
3. Выберите наибольшее и наименьшее число среди чисел
а, а2, а3, а4, а5, а6, а7 при а = – 5, а = 3.
4. Упростите выражение:
1) – х (у – 4) – 2(ху – 3) – 3х; 2) a(b + 3) – 3(2 – ab) + a.
Приведенная совокупность заданий и их последовательность охватывают все уровни усвоения знаний. Выполнение всей совокупности заданий соответствует качественному усвоению знаний и умений и может быть оценено на «отлично». Усвоению знаний и умений на уровне их применения в ситуациях, не требующих реконструкции знаний и умений, соответствуют упражнения первой группы. Правильные ответы на вопросы характеризуют усвоение знаний на уровне воспроизведения. Оценка «удовлетворительно» может быть выставлена ученику, выполнившему большинство упражнений первой группы. Оценка «хорошо» соответствует правильно выполненному большинству упражнений первой и второй групп.
Задания
1. Выберите конкретную тему коррекционно-развивающего курса алгебры основной школы. Изучите соответствующие разделы программы и учебника. Выявите методические особенности изучения темы. Разработайте фрагменты методики обучения теме. Подготовьте комплект карточек для коррекции знаний учащихся.
2. Посетите несколько уроков алгебры одного из специальных (коррекционных) учреждений VII вида вашего региона. Проведите анализ одного урока с точки зрения его образовательной, коррекционно-развивающей, воспитательной и практической направленности.
3. Одной из целей обучения математике является формирование математической культуры. Вычислительная культура – один из компонентов математической культуры. Предложите ваш вариант трактовки понятия «вычислительная культура». На каких этапах обучения математике особенных учащихся, при обучении какому содержанию возможна и целесообразна постановка цели «формирование вычислительной культуры»? Приведите конкретный пример с соответствующей системой заданий. Составьте список литературы по вопросам развития понятия о числе для внеклассного чтения особенных учащихся. Укажите, в каких классах она может быть использована.
ГЛАВА 10. ИЗБРАННЫЕ ВОПРОСЫ МЕТОДИКИ КОРРЕКЦИОННО-РАЗВИВАЮЩЕГО ОБУЧЕНИЯ ГЕОМЕТРИИ в основной школе.
